黄毅 成都大学信息科学与工程学院 模式识别与智能信息处理四川省高校重点实验室 成都大学大数据研究院 四川成都 610106

一 引言

在线性代数的教学和学习中，时常会遇到下面这样的含参数线性方程组的问题：

(1)有唯一解；(2) 无解；(3) 有无穷多解？并在有无穷多解时求出其通解。

这类问题中的方程组一般都是系数矩阵是方阵即方程个数等于未知数个数的方程组，它们的求解有一定的方法可循。但是一般的课本和参考书对这类问题的解法及其背后的理论并未给出较详细和清楚的说明，不少学生感到这类问题不好求解。本文将详细介绍这类方程组解的系数行列式判别法，并给出其理论依据。这一理论依据即本文中的定理在一般的线性代数课本中并未明确给出，但结论本身却非常重要。

二 判别定理

我们首先给出本文的主要定理。

对于一般的线性方程组Ax = b，解的判别由系数矩阵A的秩r(A)和增广矩阵以及未知数的个数n三者的大小关系来确定[1]。当线性方程组的方程个数等于未知数个数时，即线性方程组的系数矩阵是方阵时，方程组解的判别可以由系数矩阵A的行列式即系数行列式A来确定，结论如下：

定理 （系数矩阵是方阵的线性方程组解的系数行列式判别定理）

设A是方阵，则：

证明

只需证明(a)即可，(b)和(a)是等价的命题。

评论：

(一)这一定理专门适用于方程个数等于未知数个数的线性方程组解的判别；

(二)注意到(a)其实就对应着克莱姆法则。克莱姆法则是(a)中从左推出右这一结论，即A≠0⇒线性方程组Ax = b有唯一解。结论(a)说明，克莱姆法则可以补充叙述为充要条件。而一般的课本中只介绍了克莱姆法则，所以结论(a)弥补了课本的这一缺陷；

（三） 定理的结论适用于方程个数等于未知数个数的任意线性方程组，包括齐次线性方程组和非齐次线性方程组。对于齐次线性方程组的特殊情形，我们相应的有下面的推论。

定理在b=0的特殊情况下，即在齐次线性方程组的情形时，就成为：

推论 设A是方阵，则：

(I)A≠0⇔齐次线性方程组Ax=0只有零解

(II)A=0⇔齐次线性方程组Ax=0有非零解

在一般的课本中都有针对齐次线性方程组的这一推论的结论，但对于适用于非齐次线性方程组的前面定理的结论却不多见，而它正是用系数行列式方法解决这类含参数线性方程组问题的理论依据。

三 问题的求解

下面我们就用增广矩阵的初等变换法和前面定理的系数行列式判别法两种方法来求解本文最开始提出的问题，之后再求解另一个含参数线性方程组的问题。这两个问题都来自文献中的习题。我们会看到，一般情况下系数行列式判别法比初等变换法更简捷。

(1)有唯一解；(2) 无解；(3) 有无穷多解？并在有无穷多解时求出其通解。

分析

注意问题1和下面的问题2实际上是要分别寻找方程组有唯一解、无解和有无穷多解的充分必要条件，而不仅仅是充分条件。

解法一：初等变换法

解法二：系数行列式法

因为本题的方程组是方程个数等于未知数个数的方程组，所以可以利用第二节的定理来求解。

首先要计算出系数行列式A ：

（注意，计算此行列式可以采用先将第2列和第3列都加到第1列的方法）

于是根据第二节的定理有：

(1) 当λ≠-2且λ≠1时，A≠0，此时方程组有唯一解；

(2) 当λ=-2或λ=1时，A=0，此时方程组可能无解，也可能有无穷多解，具体是什么情况还需要分别把这两个数代进去计算一下才知道。下面就分这两种情况来讨论。

(2-1) 当λ=-2时，增广矩阵为

(2-2) 当λ=1时，增广矩阵为

综上所述，

(a) 当λ≠-2且λ≠1时，方程组有唯一解；

(b) 当λ=-2时，方程组无解；

(c) 当λ=1时，方程组有无穷多解，其通解为

评论：

比较解法一和解法二，可以看出，解法一带着字母λ作初等行变换，计算和讨论比较繁琐。解法二思路清晰，计算和讨论相对简单一些。

我们再来看一个例子。

问题2

（注意，这种类型的题目系数行列式是带有字母的行列式，其计算有时也会有一定的难度，直接用对角线法则展开计算可能会比较繁琐，展开后还要分解因式，也可能并不好分解。这时，我们可以仔细观察行列式的特点，利用行列式的性质化简。为化简行列式，一个目标就是需要让行列式产生0。注意到|A|的第二行第一列元素是2，第三行第一列元素是-2，可以让第二行加到第三行先产生一个0，这时会发现第三行还产生出公因子1-λ，提出这个公因子之后，计算一下就变得简便起来）

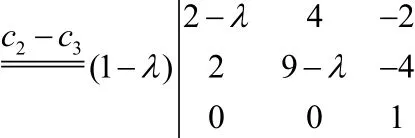
（提出公因子1-λ之后，注意到第三行第二列是1，第三行第三列也是1，可以让第二列减去第三列再产生一个0，这时第三行就有了两个0，此时将行列式按第三行展开即可）

r(A)=2，r(B)=3，系数矩阵的秩和增广矩阵的秩不相等，所以此时无解。