关于Frobenius-Euler多项式的高阶卷积公式
2018-10-10莫亚龙何圆
莫亚龙,何圆
(昆明理工大学理学院,云南 昆明 650500)
1 引言及主要结果
当研究幂和问题时,瑞士数学家Jacob Bernoulli(1654-1705)和Leonhard Euler(1707-1783)分别发现存在序列多项式{Bn(x)}Nn=0和{En(x)}Nn=0能提供前n个自然数的k次幂和与前n个自然数的交替k次幂和的统一公式.[1-4]这些多项式Bn(x)和En(x)分别被称为Bernoulli多项式和Euler多项式,它们通常由如下生成函数定义:

特别地,有理数Bn=Bn(0)和整数En=2nEn(1/2)分别被称为Bernoulli数和Euler数.
以上Bernoulli数及其多项式和Euler数及其多项式在数学的不同领域中扮有重要作用,许多学者研究了它们的算术性质,得到了极多有趣的和重要的结果.譬如,令{fn(x)}Nn=0是一个多项式序列,

其中 l1,···,ld,n是非负整数,

基于文献 [5-7]对 Bernoulli数乘积的和式公式的研究,在 1996年,文献 [8]研究了 (3)式中fn(x)=Bn(x)和fn(x)=En(x)的情形,并得到了Bernoulli多项式和Euler多项式的如下高阶卷积公式:对于正整数d,n满足n≥d,

对于正整数d和非负整数n,

其中

和s(n,d)是第一类Stirling数.在2018年,文献[9]研究了高阶zeta函数的算术性质,发现高阶zeta函数在非正整数处的值能由(3)式中fn(x)=Bn(x)的情形确定,并建立了Bernoulli多项式的一个高阶卷积公式:


鉴于以上文献的研究成果,本文将对Frobenius-Euler多项式做进一步的研究.通过运用生成函数思想和组合技巧,建立了 Frobenius-Euler多项式的一个高阶卷积公式.作为应用,Dilcher的高阶卷积公式(5)被作为特殊情况得到.
定理 1.1 令d是一个正整数,m,n是非负整数.若y=x1+···+xd,则有

其中Hn(x|λ)是 Frobenius-Euler多项式,且由如下生成函数给定(参见文献[11-12]):

这里λ是一个复数且 |t|<π当λ=−1和|t| 特别地,在定理1.1中取λ=−1,得到Euler多项式的如下高阶卷积公式: 其中 d是一个正整数,m,n是非负整数,和 y=x1+···+xd.明显地,(8)式中m=0的情形即为Dilcher的公式(5).类似地,定理1.1中m=0的情形给出了Frobenius-Euler多项式的Dilcher型高阶卷积公式,其在λ=−1处再次给出Dilcher的公式(5). 在给出定理1.1的证明之前,需要接下来的几个辅助结果. 引理 2.1令n是一个非负整数.那么对于复参数λ和α, 和对于正整数n, 证明 参见文献[13]. 引理 2.2令n是一个非负整数.则 对于正整数r, 其中⟨x⟩n是 Pochhammer符号被给定为: f(y,t)和g(y,t)分别被给定为: 这里F(t)是一个幂级数. 证明 参见文献[14]. 显然,在引理2.1的第二个公式中取α=1,并将n替换为d,可得 令 y=x1+···+xd.若在以上等式的左右两边都乘以 (1−λ)de(x1+···+xd)t,则有 根据(9)式可得 对(11)式的左右两边关于t作m次求导,根据广义Leibniz法则(参见文献[15]),可得 清楚地,由(10)式知, 对于非负整数n,令[tn]f(t)表示f(t)中tn项的系数.明显地, 在引理2.2的第一个公式中取定 则有 于是,应用(15)式到(14)式的右边,可得 根据(16)式,有 因此,将(17)式中λ替换为1/λ即得(7)式.这便完成了定理1.1的证明. 事实上,用证明(7)式的类似方法,也能建立Bernoulli多项式的如下高阶卷积公式: 其中 d是一个正整数,m,n是非负整数满足 m+n≥d,和 y=x1+···+xd.显然,(18)式中 m=0的情形即为Dilcher的公式(4).(18)式中x1=···=xd=x的情形给出了 Bayad和Komatsu的公式(6)的一个等价形式.是否文献[16]中考虑的椭圆型Apostol-Bernoulli多项式和椭圆型Apostol-Euler多项式存在与(8)式和(18)式类似的高阶卷积公式呢?作者将在今后的工作中,对该话题作进一步的研究.
2 几个引理
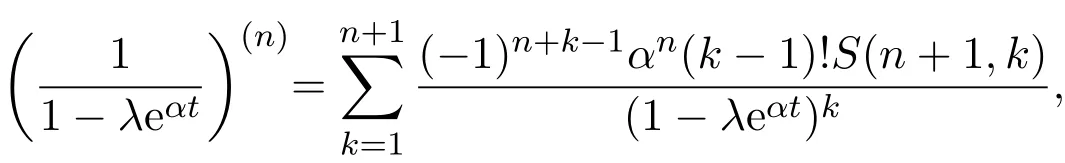



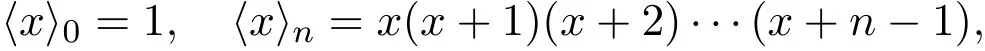

3 定理的证明











4 结束语

