Xinyue Liu, Yunqiao Liu, Xiaobo Gong, and Huaxiong Huang

Abstract: In this work, a three-dimensional axisymmetric model with nanoparticle,receptor-ligand bonds and cell membrane as a system was used to study the quasi-static receptor-mediated endocytosis process of spherical nanoparticles in drug delivery. The minimization of the system energy function was carried out numerically, and the deformations of nanoparticle, receptor-ligand bonds and cell membrane were predicted.Results show that passive endocytosis may fail due to the rupture of receptor-ligand bonds during the wrapping process, and the size and rigidity of nanoparticles affect the total deformation energy and the terminal wrapping stage. Our results suggest that, in addition to the energy requirement, the success of passive endocytosis also depends on the maximum strength of the receptor-ligand bonds.

Keywords: Receptor-mediated endocytosis, nanoparticle uptake, optimization method,receptor-ligand bonds, drug delivery.

1 Introduction

Endocytosis is a crucial biological process for cells to communicate with their environments which was widely adopted for drug delivery in biomedical engineering practices [Tanaka, Shiramoto, Miyashita et al. (2004); Brannonpeppas and Blanchette(2012); Tortorella and Karagiannis (2014)]. The success of nanoparticle uptake depends on various factors various factors, including the shape [Devika, Arezou, Ghazani et al.(2006); Decuzzi and Ferrari (2008); Vácha, Martinezveracoechea and Frenkel (2011)], size[Gao, Shi and Freund (2005); Devika, Arezou, Ghazani et al. (2006)] and rigidity [Gao,Shi and Freund (2005); Sun, Zhan, Wang et al. (2015)] of the nanoparticles, as well as the binding strength of receptor-ligand bonds [Decuzzi and Ferrari (2007); Yi and Gao (2016)].However, as a whole system for an efficient drug delivery, how these factors interact with each other, especially how the binding force determines the vesicular transport associating with the buckling of the membrane, are not clearly explained.

From the view point of energy balance, Gao et al. [Gao, Shi and Freund (2005)] initiated that the energy released by the formation of receptor-ligand bonds during the process of endocytosis compensates energy required for the bending of the wrapping cell membrane and the diffusion of the receptors from far to the wrapping region. Gao’s mechanical model helps to understand how the binding energy affects the efficiency of endocytosis at different sizes of nanoparticles, in which only bending energy of cell membranes inside the wrapping region was considered as a simplification, and the details of the mechanical characteristics of bonds were ignored. Improvement of the mechanical model for more details with considering the both deformations of the nanoparticle and cell membrane was founded in Yi et al.’s work [Yi, Shi and Gao (2011)]. Decuzzi et al. [Decuzzi and Ferrari (2007)]considered the effect of receptor-ligand bonds on endocytosis efficiency that the repulsive non-specific interaction between the nanoparticle and the cell membrane results in an increase of the wrapping time. In their study, the lengths of receptor-ligand bonds were assumed to be uniform and the rupture of the bonds was not taken into account. Yi et al. [Yi and Gao (2016)] considered stochastic receptor-ligand bonds formation, however, the receptor-ligand bonds were not allowed to rupture after formation as well.

Although the formation of various types of receptor-ligand bonds could trigger the inward wrapping on cell membrane, the characteristics of the bonds such as the life time and strength to maintain the bending of the membrane around the cargo surface may not fit the requirements for a successful uptake. The density of the receptors on cell membrane provides a gross evaluation for energy compensation, but for a specific wrapping at local region, there are more mechanical details of the receptor and ligand needs to be classified.

In this study, three main factors affecting the minimum energy required for the passive endocytosis are analyzed, which are the size of nanoparticle, the relative rigidity of nanoparticle to cell membrane, and the rupture force of receptor-ligand bonds. We assume that passive endocytosis is a quasi-static process comparing to the formation and rupture of receptors and ligands. With the energy function of the system consisting of the nanoparticle, receptor-ligand bonds and cell membrane (NRC), the minimum total deformation energy at each endocytosis stage is estimated by the optimization method, and the profile of the deformed system is obtained accordingly. In our study, the curvature difference between the nanoparticle and cell membrane at the wrapping region is described with two sets of local curvilinear coordinates respectively. The rupture of bonds with thresholds of spring forces is introduced. In this way, a more detailed limitation on the binding forces of receptor-ligand bonds for a successful uptake is analyzed and proposed.

2 Method

2.1 Energy function

Fig. 1A shows the geometry and relation between cell membrane and nanoparticle mediated by receptor-ligand bonds in an endocytosis system, in which the cell membrane is colored in blue, the nanoparticle in red and the receptor-ligand bonds in black,respectively. In order to modeling the deformation of the cell membrane and nanoparticles,a local curvilinear system,for the tangential angle andthe arc length starting from the origin were set up as shown in Fig. 1B. Fig. 1C illustrates the details of a receptorligand bond which connects the nanoparticle and the cell membrane. The cell membrane is physically modeled as a hyper elastic thin film with cytoskeleton supporting the lipid bilayer [Skalak, Tozeren, Zarda et al. (1973)]. In drug design, nanoparticles containing medicines are usually coated by ligands of a relatively high density on the surface through PEG-crosslinkers [Choi, Alabi, Webster et al. (2010)]. Fig. 1D shows the discretization of nanoparticle and cell membrane, as well as how the bonds connect. We assume that the van der Waals forces make the dense ligands perpendicular to the surface of nanoparticle,so that the receptor-ligand bonds are vertical to the nanoparticle surface in our model.

Figure 1: Schematic illustrations. (A) The NRC system. (B) Coordinate. (C) Details of the receptor-ligand bonds and cell membrane model (D) Numerical discretization of the NRC system

The relationship between (ψ,s) and the Cartesian coordinates (x,y)for the nanoparticle and the cell membrane are given by,

where l1is the length of the first receptor-ligand bond,andare the extension ratios of nanoparticle and cell membrane along the tangential direction, respectively. The extension ratio is defined as, whereandare the arc differentials before and after the deformation, respectively.

The total deformation energy function of the system is formulated and listed as follows.

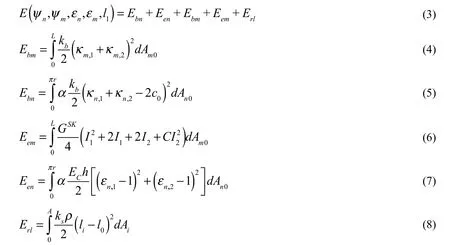
Skalak et al.’s model [Skalak, Tozeren, Zarda et al. (1973)] is used for the strain energy Eemof cell membrane,andare the strain invariants,respectively. GSK=BECh is the SK elastic modulus of cell membrane, where ECandh are the Young’s modulus and the thickness of cell membrane, respectively. B and C are the membrane material properties constants.

A linear elastic model is adopted for the small deformation of nanoparticle [David and Leibler (1991)] as Een.

Erlis a linear spring model used for the receptor-ligand bonds deformation [Dembo(1994)], in whichis the spring constant,is the density of receptor-ligand bonds,Aiis the area of wrapping region. Each receptor-ligand bond starts from the pointon the nanoparticle, stretching along the outward normal direction, and connects to the point on the cell membrane. The length of each receptor-ligand bond isas shown in Fig. 1D, and the binding force isIn the present work, a quasi-static state of the NRC system is considered. We assume the receptor-ligand bonds are at kinetic equilibrium state inside the wrapping region when the stretches of bonds are less than the maximum stretching length Δl. We do not consider the stochastic nature of bonds binding and unbinding. The ithreceptor-ligand bond ruptures when the stretching length is longer than Δl, the corresponding energyis counted in the total energy function Eq. (3). Once the bonds ruptured, a new energy function of the NRC system will be updated automatically and the new minimal energy value will be achieved at a new equilibrium state. If the distance of nanoparticle to the cell membrane is still greater thanwhere bonds ruptured, then no new bonds can be formed, and the passive endocytosis is terminated and aborted.

In addition, three equality constraint functions are imposed in estimating the minimal energy of the endocytosis system. They are the volume conservation of nanoparticle, the integrity of the geometry of nanoparticle, and the fixed computing domain of the deforming cell membrane as the follows

When the bonds are compressed to the lower length limit l0−Δl and the repulsive energies are rising, to avoid the over-approaching of the nanoparticle and cell membrane, a series of inequality constraint functions are introduced with the bonds index i as

2.2 Algorithm

Newton’s method is adopted to find the minimum of the total energy. The numbers of discrete elements on the nanoparticle surface and the cell membrane are N and M,respectively. The unknown vector isand the definition domain is

Using the Taylor expansion of energy function at x,

The gradient of energy is formulated as

Assuming the initial profileof the membrane at any pre-set stage of endocytosis, the iteration of the discretized membrane position xconverges to satisfy the minimum energy requirements following

In the present study, when both the errorand the 1-norm of constraint functions violationsare satisfied, the local minimum of energy functionis obtained.

2.3 Geometric and mechanical parameters

For the particle sizes, the minimum size D=25 nm [Gao, Shi and Freund (2005)], the optimal size D=50 nm [Gao, Shi and Freund (2005)], and size D=75 nm and 100 nm [Zhang, Gao and Bao (2015)] that usually discussed in literatures are selected. Since the nanoparticles can be fabricated by many kinds of materials [Ensign, Cone and Hanes (2014)], the rigidity of nanoparticle relative to cell membrane is represented by the Young’s modulus ratio, which varies from 0.1 (10 times softer) to 10000 (10000 times stiffer) over six orders of magnitudes.Based on the previous experimental studies, the receptor-ligand rupture force fris assigned as 2 pN for non-specific binding [Shergill, Melotykapella, Musse et al. (2012)], 20 pN for specific binding of common receptor-ligand bonds [Zhu, Long, Chesla et al. (2002)], and 200 pN for stronger specific bonds [Moy, Florin and Gaub (1994)] in our model.

The free length l0of receptor-ligand bonds is calculated form the central layers of nanoparticle shell to the cell membrane. According to the experimental observations,l0=20 nm [Cheng, Zak, Aisen et al. (2004)] and Δl=5 nm [Wong, Kuhl, Israelachvili et al.(1997)] are chosen for linear elasticity in our model. In addition, we assume that these the receptor-ligand bonds rupture at the same maximum stretching length Δl. Therefore, the spring constant ksis proportional to the rupture force fr.

In the present work, we set the density of bonds as ρ=5000 /um2based on the previous study [Chou (2007)], which leads to a successful virus entry. The arc length of the generatrix of nanoparticle in the symmetrical plane is divided equally into 6 parts. The wrapping fraction wfpresenting 6 wrapping stages is the ratio of the arc length in wrapping region to the total arc length of nanoparticle’s generatrix line.

The parameters values used in out computations are listed in Tab. 1.

Table 1: The physical constants in the model

3 Results

Fig. 2 provides a direct view of the shapes of the NRC system under various conditions.In order to avoid the effect of the initial value on the searching of minimum energy, the initial shapes of the nanoparticle and cell membrane of all 6 stages are considered to be identical as shown in Fig. 2A. The initial length of the receptor-ligand bonds is at the free length l0, and new pairs of bonds are added symmetrically to represent the going forward of the wrapping process. The numbers of bonds plotted in Fig. 2 are only as illustrations.In our simulation, the numbers of the receptor-ligand bonds are obtained through multiplying the receptor-ligand bonds density ρ by the wrapping area Ai.

Fig. 2B shows the predicted shapes of the nanoparticle and cell membrane with the energy function converged, corresponding to their initial shapes as shown in Fig. 2A at each wrapping stage, respectively. In Fig. 2B(6), the dash lines present ruptured bonds. In the present work, rupture of receptor-ligand bond is irreversible when the stretching length is larger than Δl.

Fig. 2C shows the terminal wrapping stage of passive endocytosis under various bond strength. It is shown that for the same size and rigidity of nanoparticles, receptor-ligand bonds rupture occurred at earlier stage when the rupture force is smaller, which indicates that increase of binding strength can promote the wrapping fraction.

Fig. 2D shows that as the particle size increases, bond rupture may occur at an earlier wrapping stage while the bottleneck of cell membrane that needs to be closed for a successful uptake is still quite large. It suggests that nanoparticles of larger size need stronger binding ligands for further wrapping.

Fig. 2E shows that for the nanoparticle of 100 nm, changes of the Young’s modulus ratio between nanoparticle and cell membrane do not affect much on the terminal stage of the endocytosis. It indicates that if the bond rupture is taken into account, the effect of nanoparticle size is more dominant than the rigidity on the passive endocytosis termination.

But it s hard to hide a full 60 foot crane in your day to day trash. You could hide a 20 foot crane, or a 30 foot crane. But a 60 foot crane is just too big to easily hide in the trash.

Figure 2: Profiles of the NRC system. (A) The initial shapes of the system with D=25 nm,α=100 and fr=20 pN at each wrapping stage. (B) The optimized shapes of the system with the same parameters as (A) at each wrapping stage. (C) Rupture forces effect on the system profiles with D=50 nm and α=100 at the terminal wrapping stage when bonds rupture occurred. (D) Size effect on the system profiles with α=100 and fr =20 pN at the terminal wrapping stage. (E) Rigidity effect on the system profiles with D=100 nm and fr=200 pN at stage 5th

Fig. 3 provides a checking map of the binding forces of receptor-ligand bonds in wrapping region. The contours represent the ratio of binding force to rupture force fi/fr. The color bar (red, blue and yellow) indicate the over-stretched rupturefi/fr=1, over-compressing fi/fr=−1and at the free length of bonds fi/fr=0, respectively.

Fig. 3A shows the deformed cell membrane in the wrapping region at each wrapping stage colored by fi/fr. The bonds are most likely to rupture at the outer edge of the wrapping region as they stretch more than those inside; meanwhile, there are some bonds compressed inside the wrapping region.

Fig. 3B is the folding of shapes with contour at each stage in Fig. 3A into lattices. In this parameter combination, the receptor-ligand bonds rupture when the wrapping moves from 5thstage to 6thstage, so the lattice of wrapping fraction from 5/6 to 1 is half colored.

Due to the symmetry, Fig. 3C is the further folding of the right half half in Fig. 3B, and the location is shown in a black box plotted in Fig. 3D.

In Fig. 3D, the lattices are divided into 3 large groups horizontally according to the rupture force of the receptor-ligand bonds, and wrapping fraction 1/6～6/6 in each group represents six wrapping stages, respectively. The lattices are also divided vertically into 4 large groups according to the sizes of nanoparticles, and 6 small groups of different rigidities. The partially colored lattices in the Fig. 3D represent receptor-ligand bonds ruptured and the passive endocytosis terminated. As shown in Fig. 3D, the smaller the rupture force causes earlier rupture stages, especially for the non-specific binding group fr=2 pN, this kind of nanoparticles are designed for stealth liposome to avoid the reticuloendothelial system[Needham, Hristova, McIntosh et al. (2008)]. The fr=20 and 200 pN groups are referred to specific binding ligands for the targeting drug, which is an improvement of drug delivery based on anchored stealth liposome for specific site on cancer cell [Paliwal, Paliwal,Mishra et al. (2010)]. Our results suggest that specific binding ligands can improve the process of nanoparticles engulfed by cell, but they alone cannot guarantee the completion of passive endocytosis.

Figure 3: The contours of binding force to rupture force of the receptor-ligand bonds. (A)The contours correspond to the cell membrane shapes with D=25 nm, α=100 and fr=20 pN at each wrapping stage. (B) Folding of (A) into lattices. (C) Further folding according

to the symmetry (D) The ratio of bind force to rupture force of the receptor-ligand bonds covering all of the cases in this study

Fig. 4A shows the energy consumption increases with the wrapping fraction grows before endocytosis terminates. The curves are classified in 3 groups according to the rupture force.Before terminated, the curves show no obvious difference, which indicates the different rupture forces determine the different terminal wrapping fractions but do not affect so much on energy consuming increasing.

Fig. 4B provides a more intuitive view of the exponential increases of energy consuming as the developing of wrapping process. The blank lattices correspond to the terminal wrapping fraction in Fig. 3. The 4 boxes (1-4) are corresponded to the subplots plotted in Fig. 4C.

Fig. 4C shows more details of the energy consuming affected by the rigidities. The subplots(1-4) are corresponded to the 4 boxes plotted in Fig. 4B and the colors representing different rigidities in each energy bar are consistent to the legend in Fig.4A. The energy consuming of particles rigidity with α=10000 are always the highest as shown in Fig. 4C.This indicates that when the rigidity of particle reaches to a certain degree, the increment of the energy consuming is relatively higher, despite the deformation of the nanoparticles is less insignificant. Since the synthetic capsules are usually stiffer than the cell membrane,our results suggest that using softer material for drug synthesis is preferable. When D and frare fixed, the lowest energy consuming always corresponds to the α=0.1 cases, due to the fact that it is easier for softer nanoparticles to adapt to the deformation of cell membrane envelope (see Fig. 2E). This result suggests that it is worth further exploring the innerrelated between natural low rigidity and the high entrance efficiency of bacteria and viruses entering the host cells [Cureton, Harbison, Cocucci et al. (2012)]. The synthetic nanoparticle rigidity is moderate within 1≤α≤100, while the energy consuming seems not necessarily positive-correlated with the particle rigidity increasing at each group as shown in Fig. 4C. This indicates when both size and rupture force are considered, the optimal rigidity of nanoparticles falls within 1≤α≤100. Yi et al. [Yi and Gao (2016)] compared the stiffness ratio of nanoparticle and cell membrane in the range of 0.1≤α≤1 and showed that stiffer particles achieved full internalization slightly faster than a softer particle. Sun et al. [Sun, Zhan, Wang et al. (2015)] showed that that when the ratio falls in 10＜α＜100,stiffer nanoparticles have a slightly higher uptake rate than the softer ones, because softer nanoparticles were easier to deform and relatively difficult for cellular uptake. In addition,none of them considered the rupture force of receptor-ligand bonds. As a result, more experimental evidences need to be collected.

Fig. 4D shows that the energy components of the cell membrane increase with wfgrows,while the energy components of the nanoparticle may decrease. A detail energy components are shown in Fig. 4E that the energy component of the receptor-ligand bonds is significant when wf≤1/3, because the total energy consuming is low at the earlier stages.

However, the energy of the bonds can be ignored at later wrapping stages even if the binding forces are relatively larger. This result indicates that the over-stretching or overcompressing of receptor-ligand bonds is not a major contribution to the total energy consuming; instead, it is the large deformation of cell membrane that causes high energy consuming. For nanoparticles with α≥100 (e.g. Fig. 4F), wf=1/2 is a turning point.

Before reaching this point, energy components of nanoparticle decrease and beyond this point, the energy increase. This is due to two main reasons. One is that extremely stiff nanoparticles cause more deformation energy as discussed above, and the other is that receptor-ligand bonds mediate the nanoparticle and cell membrane interaction. At the later stages, more bonds are formed with larger stretch length, and the nanoparticles are pulled or extruded by the bonds in every direction.

Figure 4: The variation of energy of the NRC system at different parameters. (A) The deformation energy of the NRC systems

Figure 4: (B) The log spectrum scale of the minimum deformation energy covering all of the cases in this study

Figure 4: (C) Rigidity effect on the system deformation energy

Figure 4: (D) Energy components. (E) Details of energy components with D=25 nm,fr=20 pN, and α=10. (F) Details of Energy components with D=50 nm, fr=200 pN, and α=10000

Fig. 5A shows a heat map of the termination of passive endocytosis because of the shortage of energy supply. Here, we assume that the energy consuming for the NRC system is all transferred from the chemical energy released by the binding of the receptor-ligand bonds,without considering the thermal dissipation. The chemical energy released by the receptorligand bonds needs to compensate the deformation energy increasing during wrapping. In the present work, 6 stages of wrapping are investigated, and the approximationis used. Passive endocytosis is unable to continue when ΔE/ΔA＞ ΔG/ΔA, where ΔGis the change of Gibbs free energy in the binding of receptor-ligand bonds. For fr=200 pN group, Moy et al. [Moy, Florin and Gaub(1994)] measured the change of Gibbs free energy in the binding of avidin-biotin bonds by atomic force microscopy (AFM). For fr=20 pN group, Fotticchia et al. [Fotticchia,Guarnieri, Falanga et al. (2016)] used isothermal titration calorimetry (ITC) to measure the Gibbs free energy change in the binding of transferrin and its receptor (Tf-TfR). According to these previous studies, two referenced lines (Avidin-biotin and Tf-TfR) are shown in Fig. 5A. Despite no data can be referred to the non-specific group currently, a lower energy reference line than Tf-TfR group should be and we do not discuss in this work.

The combination of two criteria blocking the passive endocytosis progress is shown in Fig.5B. The green lattices correspond to the terminal wrapping fractions in Fig. 3D. The red line in fr=20 pN group is corresponded to energy reference line of Tf-TfR bonds, and in fr=200 pN group is corresponded to avidin-biotin bonds, respectively. This figure suggests that all of the passive endocytosis cannot complete in our model, and additional mechanism should be considered in further research.

Figure 5: Diagram of the terminal wrapping stage for the passive endocytosis. (A) Energy increment per area of log scale

Figure 5: (B) Two criteria for the passive receptor-mediated endocytosis

4 Discussion

A direct Newton’s method is used to obtain the minimum deformation energy of the NRC system. Each wrapping stage is independently solved, such that the computation can be carried out at the same time with various parameter combinations. This method is computational efficient, especially when the total number of parameters permutations and combinations is large. The disadvantage of our approach is the hypothesis of quasi-static process, which does not allow for the consideration of the time scale. As a result, the time required for the dynamic endocytosis has not been investigated. As the quasi-static assumption is adopted in this study, we do not consider the stochastic process. Instead, we focus on the elastic potential energy stored in the receptor-ligand bonds after the formation.The deformation of cell membrane is not identical to the nanoparticle in the wrapping region, because the length of the receptor-ligands bonds is not uniform distribution in our model, which is different from the models of Yi et al. [Yi, Shi and Gao (2011); Decuzzi and Ferrari (2007)]. Meanwhile, the effect of receptor-ligand bonds rupture during the passive endocytosis is also taken into account in our model.

In Fig. 3, when the receptor-ligand bonds ruptured during wrapping and a new equilibrium state of the NRC system is achieved, if the distance of nanoparticle to the cell membrane is still larger than l0+Δl, then no new bonds can be formed, which leads to the termination of passive endocytosis. Hence, a force criterion to determine the success of passive endocytosis depend on whether the receptor-ligand bonds can provide enough binding force to overcome rupture, which can be directly obtained by optimization method.According to the force criterion, cells need to provide additional force to help the cell membrane move closer to the wrapping region to complete the endocytosis process where the receptor-ligand bonds fail to provide enough binding force, in that case the endocytosis may shift from passive to active mechanism. Liu et al. [Liu, Kaksonen, Drubin et al. (2006)]calculated the extra force required to complete endocytosis at the last (necking) stage aiding by special proteins in the cytoplasm such as dynamin.

In Fig. 5A, the receptor-ligand bonds cannot to provide enough chemical energy to compensate the large energy increment during wrapping even if the binding forces are adequate, which may also result in the termination of passive endocytosis. Therefore, an energy criterion for a successful passive endocytosis process is proposed, which is indirectly obtained because it is based on an approximate estimation of previous experiment data. It is worth emphasizing that the energy criterion in the present work is different from the energy balance in Gao and Yi’s works [Gao, Shi and Freund (2005); Yi and Gao (2016)], in which the energy supply is always enough because they assumed once a new receptor diffused to the edge of wrapping region can always have opportunity to bind to ligands on the nanoparticle, and the bonds are closed at a certain length without rupture after formation, the completion of endocytosis is only a time problem. According to the energy criterion, one potential method to increase binding energy is to coat the nanoparticle surface with ligands that can release more chemical energy when forming the bonds. It is not always possible, because the choosing ligands are depended on the specific receptors on cancer cells. Another approach is to increase the receptor-ligand bonds density,which also has limitation because it is depended on both of the receptors density on the cell membrane and the ligands density on the nanoparticle surface. Here a simple chemical reaction equationis used to describe the reversible reaction of receptorligand in wrapping region, andthe kinetic equation.According to the experimental data of the forward kfand reverse krkinetic rate constants in the work of Chesla et al. [Chesla, Selvaraj and Zhu (1998)], whenan approximately maximum estimation is conducted thatρ≤0.3%ρl, where ρlis the ligand density. In practice, ρl＞1500000 /um2also seems impossible. Consequently, there exists an energy barrier for passive endocytosis.

By combing the two criteria, merely relying on the chemical energy and binding force provided by the receptor-ligand bonds may not guarantee the success in passive endocytosis. Cells need to supply additional force and energy. This is practically feasible,because there does exist the active mechanism of endocytosis in cells, such as the clathrincoated pits formed beneath the cell membrane, which can assist cargos entering the cells[Higgins and Mcmahon (2002); Loerke, Mettlen, Yarar et al. (2009)]. Interestingly, it is reported that endocytosis is randomly initiated and then stabilized by clathrin-coated pits[Ehrlich, Boll, Van et al. (2004)]. Our next research project is to consider the role of the clathrin-coated pits in endocytosis.

5 Conclusions

In this paper, a three-dimensional axisymmetric model was established for the quasi-static endocytosis process in which the spherical nanoparticles were engulfed by the cell membrane. By using a direct method to minimize the energy function of the NRC system,we analyzed how passive endocytosis affected by the particle size, particle rigidity, and the strength of the receptor-ligand bonds.

Our results show that the total energy of the NRC system during the endocytosis increases with the wrapping region. Nanoparticles with larger size need to be coated with stronger binding ligands. Under given particle size and bond rupture force, there exists an optimal range for nanoparticle rigidity. More importantly, at the terminal stages of passive endocytosis, receptor-ligand bonds at the edge of the wrapping region break due to limitation of the rupture force, which preventing the completion of passive endocytosis.

We proposed two criteria for successful passive endocytosis: 1) The bonds per unit area need to provide sufficient energy; and 2) The bonds need to be sufficiently strong. Passive endocytosis cannot be completed when either the energy or force provided by the receptorligand bonds is insufficient. Therefore, the completion of endocytosis requires the cells to provide extra energy and force through active mechanisms.

Acknowledgement:This work was supported by the National Natural Science Foundations of China (11372191, 11232010) and the Natural Science and Engineering Research Council of Canada.