Yanxia Wang, Yu Wang, Siqi Li, Aziz ur Rehman Aziz, Shutian Liu and Kairong Qin,

Abstract: Assessment of the magnitude and pattern of wall shear stress (WSS) in vivo is the prerequisite for studying the quantitative relationship between exercise-induced WSS and arterial endothelial function. In the previous studies, the calculation of the WSS modulated by exercise training was primarily based upon the rigid tube model, which did not take non-linear effects of vessel elastic deformation into consideration. In this study,with an elastic tube model, we estimated the effect of a bout of 30-minute acute cycling exercise on the WSS and the flow rate in the common carotid artery according to the measured inner diameter, center-line blood flow velocity, heart rates and the brachial blood pressures before and after exercise training. Furthermore, the roles of exerciseinduced arterial diameter and blood flow rate in the change of WSS were also determined.The numerical results demonstrate that acute exercise significantly increases the magnitudes of blood flow rate and WSS. Moreover, the vessel elastic deformation is a non-negligible factor in the calculation of the WSS induced by exercise, which generates greater effects on the minimum WSS than the maximum WSS. Additionally, the contributions of exercise-induced variations in blood flow rate and diameter are almost identical in the change of the mean WSS.

Keywords: Acute cycling exercise, blood flow, wall shear stress, common carotid artery,elastic tube model, rigid tube model.

1 Introduction

Wall shear stress (WSS), the frictional force of flowing blood acting on the vascular endothelium, plays pivotal role in the improvement of endothelial function and cardiovascular health [Thijssen, Schreuder, Newcomer et al. (2015)]. In physiological condition, the pattern and magnitude of WSS can be affected by geometrical shape and location of vessel. Curved, bifurcated and stenosis arteries create oscillatory flow and low mean WSS environment [Akbar (2016); Estrada, Giridharan, Nguyen et al. (2011)].These WSS conditions induce the occurrence and development of endothelial dysfunction and atherosclerosis due to the increase of endothelial cell membranes permeability and higher expression of inflammatory factors (e.g. monocyte chemotactic protein-1, MCP-1,intracellular adhesion molecule, ICAM-1, and so on) [Galkina and Ley (2007); Chen,Zhang, Qiu et al. (2017); Sanabria and Dong (2018)]. In contrast, normal and high laminar shear stress in straight arteries can promote the production of nitric oxide (NO)and prostacyclin (PGI2), which can provide beneficial effects for improving the endothelial function and protecting the endothelium from atherosclerotic disease [Hsieh,Liu, Huang et al. (2014)].

Exercise training can increase the blood flow rate and mean WSS in arteries to meet the body oxygen demand, which are beneficial for arterial endothelial function [Taylor,Cheng, Espinosa et al. (2002)]. Birk et al. [Birk, Dawson, Atkinson et al. (2012)]indicated that acute lower limb cycle training improved brachial artery endothelial function attributed to the increase of WSS. Green et al. [Green,Bilsborough, Naylor et al.(2005)] suggested that oscillatory shear stress caused by acute cycling exercise possibly mediated the release of NO. Hambrecht et al. [Hambrecht,Adams, Erbs et al. (2003)]demonstrated that four weeks regular aerobic exercise training elevated the expression and phosphorylation of endothelial nitric oxide synthase (eNOS) in left internal mammary artery. Collectively, these findings indicated that reasonable exercise training,including acute and chronic exercise training could improve arterial endothelial function mainly attributed to the changes of WSS amplitude or pattern.

Evaluation of the magnitude and pattern of arterial WSS in vivo is indispensable for studying the quantitative relationship between exercise-induced WSS and arterial endothelium function. The arterial WSS in vivo can be estimated by means of noninvasive and precise magnetic resonance imaging or Doppler ultrasound technique[Taylor,Cheng, Espinosa et al. (2002); Simmons, Padilla, Young et al. (2011)]. For the superficial arteries, e.g. common carotid artery and brachial artery, the blood flow rate is usually assessed with the inexpensive Doppler ultrasound technique. For instance,Simmon et al. [Simmons, Padilla, Young et al. (2011)], Johnson et al. [Johnson,Mather,Newcomer et al. (2012)], and Tanaka et al. [Tanaka, Shimizu, Ohmori et al. (2006)] used the Doppler ultrasound to measure the diameter and blood flow velocity of the brachial artery before, after, or during exercise training to calculate the mean blood flow rate and mean wall shear rate (WSR). Liu et al. [Liu, Yuan, Qin et al. (2015)] and Yuan et al.[Yuan,Liu, Gao et al. (2016)] also adopted the Doppler ultrasound technique to measure the waveforms of arterial diameter and center-line blood flow velocity to determine the arterial WSS in common carotid arteries following acute or chronic exercise training.

It is worth noting that all these previous investigations, for calculating the exerciseinduced WSS or WSR, were based upon the hypothesis that the arterial wall was rigid[Simmons, Padilla, Young et al. (2011); Johnson,Mather, Newcomer et al. (2012);Tanaka, Shimizu, Ohmori et al. (2006); Liu, Yuan, Qin et al. (2015); Yuan,Liu, Gao et al.(2016)], which did not accord with the actual physiological conditions. In arteries,vascular walls experience elastic deformations caused by the cardiac cycles and other physiological or physical activities, such as exercise training, and the interactions between these elastic deformations and pulsatile blood flow may lead to significant effects on the arterial WSS. Consequently, the previous estimations of WSS or WSR based on the rigid tube model were not precise enough in that case where the vessel elastic deformations were ignored. A number of studies [Chien, Skalak and Usami (1998);Fisher, Chien, Barakat et al. (2001); Chien (2007)] have corroborated that endothelial cells are sensitive to WSS amplitude and pattern, and they can precisely discern the changes in the characteristic values of WSS, including maximum, mean and minimum WSS, as well as oscillatory shear index (OSI), negative index (NEG), and relative residence time (RRT). Accordingly, more accurate assessment of the arterial WSS, based on the non-linear effects of vessel elastic deformations, is of great importance, which can be helpful in recognizing the impact of exercise-induced WSS on endothelial function and further understanding its underlying molecular mechanisms.

In the arterial bed, common carotid arteries are the main arteries supplying blood to the brain that are identified as the detection window of cerebrovascular function. The improvements in their endothelial functions are associated with the decrease in risks of hypertension, atherosclerosis, and stroke [Lusiani, Visona and Pagnan (1990)]. Various studies have demonstrated that acute or chronic exercise trainings obviously affect the arterial WSS patterns and significantly increase the OSI based on the rigid tube model[Liu, Yuan, Qin et al. (2015); Yuan, Liu, Gao et al. (2016)]. However, the WSS waveform patterns and characteristic values of the common carotid arteries in response to exercise training based on the elastic tube model have not been reported yet. Moreover,the roles of arterial diameter and flow rate variation affected by the exercise in the change of WSS are also unknown.

In order to solve the above-mentioned problems, we measured the inner diameter and the center-line blood flow velocity of the right common carotid artery with a color Doppler ultrasound (ProSound Alpha 7, Aloka), and synchronously measured the heart rate,brachial systolic and diastolic pressures with an electronic sphygmomanometer (Patient Monitor PM8000, Mindray) in resting state and immediately after acute aerobic cycling exercise. Then, based on the elastic tube model, we quantified the waveforms and characteristic values of the flow rate and WSS before and immediately after exercise using the above measured hemodynamic variables. Moreover, we evaluated the effect of acute aerobic cycling exercise on WSS and determined the roles of the arterial diameter and flow rate in the variations of WSS. In addition, the above characteristic values were compared with those acquired values based on the rigid tube model to estimate the differences of exercise-induced wall deformations on WSS.

2 Materials and methods

2.1 Subjects

Twelve healthy male university students (aged: 24 yr±2 yr, height: 173 cm±2 cm, weight:69 kg±5 kg) were recruited from the Dalian University of Technology. No subject had cardiovascular diseases or other symptoms, such as hypertension, hyperglycemia, or hyperlipidemia. No subject was taking any cardiovascular drug during the experiment.The study was approved by the Ethics Committee of Dalian University of Technology.Written informed consents were acquired from every subject before participation.

2.2 Experimental procedure

Subjects were instructed to rest on a detected-bed in the supine position for 15 min prior to measurement. The center-line blood flow velocity and inner arterial diameter waveforms were measured on the 1 cm-1.5 cm before the bifurcation of the right common carotid artery using a color Doppler ultrasound (ProSound Alpha 7, Aloka). The heart rate and the blood pressure of the brachial artery in resting state were measured using an electronic sphygmomanometer (Patient Monitor PM8000, Mindray). After that, subjects carried out a bout of 30 min cycling exercise (Powermax-VIII, Combi Wellness) at a workload corresponding to about 60% maximum heart rates and then immediately, subjects resumed the supine positions for the measurements of their heart rates, blood flow velocities, arterial diameters and blood pressures according to above mentioned measurement methods. All these measurements were conducted by the same well-trained operator.

2.3 Calculation of hemodynamic variables

2.3.1 WSS and flow rate

A) Elastic tube model

The common carotid artery was treated as an isotropic, thin-walled, and elastic circular tube, and the pulsatile blood flow in it was treated as incompressible Newtonian fluid flow. The governing equations representing the pulsatile blood flow in the elastic circular tube were simplified as follows [Berbich, Bensalah, Flaud et al. (2001); Ling and Atabek(1972)]:

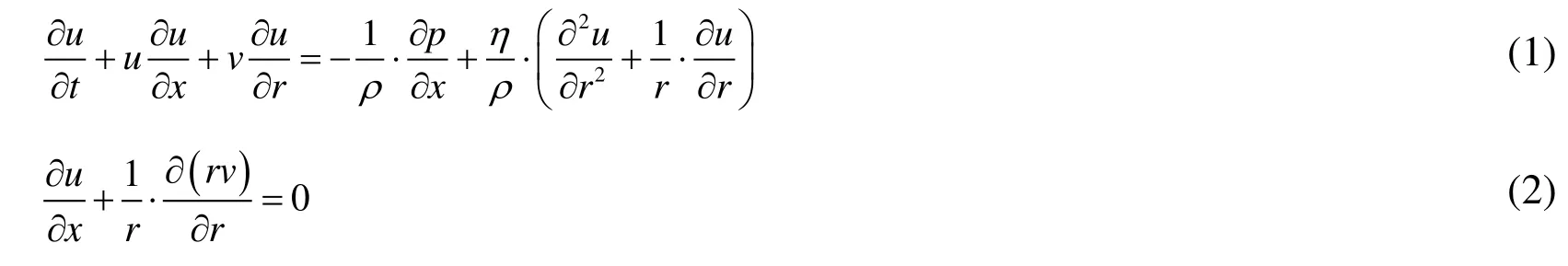
where, t is the time, u represents the axial velocity, v represents the radial velocity, p is the blood pressure, η is the blood viscosity, ρ is the blood density, and x and r denote longitudinal and radial coordinates, respectively.

The boundary conditions were as bellows:

where, R is the inner radius of the common carotid artery.

A relative radical coordinate y=r/R was introduced into Eq. (1), so the radial distribution of the axial velocity in the straight artery was expressed as:

Assuming that a small variation in x did not change the shape of the axial velocity profiles, so the longitudinal gradient of the axial velocity u satisfied the following equation:

where, f(x, t) is the function of x and t. By introducing Eq. (6) into Eq. (2), the radial velocity was expressed as:

where, ucis the center-line blood velocity of the artery.

The radial velocity v was derived from Eqs. (7)-(9) as:

The axial velocity u and the radial velocity v were deduced from Eqs. (5), (9) and (10).

Then, the axial shear stress and radial shear stresswere expressed as:

Because of the radial shear stresswas far less than the axial shear stress, the total shear stressat the time t was approximated as:

The flow rate was calculated as:

B) Rigid tube model

Note that while the common carotid artery was modeled as a rigid circular tube in the case where the vessel elastic deformation is ignored, the flow rate was calculated as follows [Liu, Yuan, Qin et al. (2015)]:

Here, n is the harmonic number,，R0is the time-averaged value of the carotid artery radius in a cardiac cycle,, T is the duration of one cardiac cycle,J0and J1are the 0th-order and 1th-order Bessel function of the first kind,is the Womersley number, and ωn=2nπ/T is angular frequency. In Eq. (16),was the n-th harmonic component of the measured center-line velocity, uc(t), and satisfied the following equation [Liu, Yuan, Qin et al. (2015)]:

2.3.2 Variables for WSS patterns

Oscillatory shear index (OSI) represented the oscillation degree of flow reversal, which was calculated as follows [Ku, Giddens, Zarins et al. (1985)]:

Negative index (NEG) stood for the oscillation duration of flow reversal, which was determined by the duration of retrograde flow (Tre) dividing by the total duration of one cardiac cycle (T) [Estrada, Giridharan, Nguyen et al. (2011)]:

Relative residence time (RRT) was a useful measurement of the oscillatory shear environment for correlative purposes, which synthesized the level of the shear stress and its oscillatory character [Himburg, Grzybowski, Hazel et al. (2004)]:

2.4 Numerical computation and statistical analysis

Based on the measured center-line velocity, arterial diameter, as well as brachial arterial blood pressure, the flow rate, WSS, OSI, NEG, and RRT are numerically computed using the above Eqs. (1)-(20). For the elastic tube model, there was a linear relationship between the changes in vessel diameter and blood pressure within each cardiac cycle, i.e.the vessel diameter waveform was similar to pressure waveform [Sodolski and Kutarski(2007)]. Moreover, the mean values of carotid arterial pressure pmand diastolic pressure pdwere approximately equal to the mean values of brachial pressure pm-meaand diastolic pressure pd-mea[Hoetink, Faes, Visser et al. (2004)]. Thus,was calculated by following equation:

where pdand Rdare the diastole blood pressure and the corresponding carotid arterial radius, respectively. The mean blood pressure pmwas calculated by following equation[Heffernan, Jae, Wilund et al. (2008)]:

here, ps-meais the systolic blood pressure of brachial arterial. Therefore,was determined and the carotid artery blood pressure waveform could also be acquired.Finally, the pressure gradientwas numerically calculated by Eq. (9). Once the pressure gradientwas obtained, the radial velocity v and the axial velocity u were numerically solved from Eqs. (5), (9) and (10). The WSS and the flow rate were finally calculated by Eqs. (13) and (14), respectively. In all the numerical simulations by the elastic tube model, the finite difference schema was adopted as similar as in the literatures [Berbich, Bensalah, Flaud et al. (2001); Ling and Atabek (1972)]. For the rigid tube model, the flow rate and the WSS were directly calculated by Eqs. (15) and (16).The blood flow in the common carotid artery was modeled as a Newtonian fluid with the blood viscosity and density for all the subjects of 4 mPa·s and 1050 kg/m3, respectively[Liu, Zhao, Wang et al. (2016)].

SPSS 18.0 software was used to conduct the data analysis. All the hemodynamic parameters were expressed as means ± standard deviation (SD). p<0.05 was set to denote the significance differences. The paired t-test was used to assess the differences of hemodynamic variables between resting state and immediately after exercise and to compare the difference of the same hemodynamic variables based on the elastic and rigid tube models.

3 Results

3.1 Effect of acute cycling exercise on the waveforms of arterial diameter, center-line velocity, flow rate and WSS in the common carotid artery

As shown in Tabs. 1, 2 and 3, considering that the maximum, mean and minimum of arterial diameter, center-line velocity, flow rate and WSS in twelve subjects following acute cycling exercise statistically increase or decrease, the typical waveforms of them from a representative subject in resting state and immediately after exercise are depicted in Fig. 1. It is clear that the waveform of post-exercise arterial diameter is shifted down (Fig.1a) while the post-exercise center-line velocity is moved up in contrast to those in resting state (Fig. 1b). In addition, the waveforms of flow rate and WSS immediately after exercise are amplified, which specifically display that the peak points of the waveforms are elevated and the valley points of the waveforms are decreased (Figs. 1c and 1d).

Figure 1: Arterial diameter (a), center-line velocity (b), flow rate (c, calculated) and WSS (d, calculated) during one cardiac cycle of a representative subject in resting and immediately after exercise

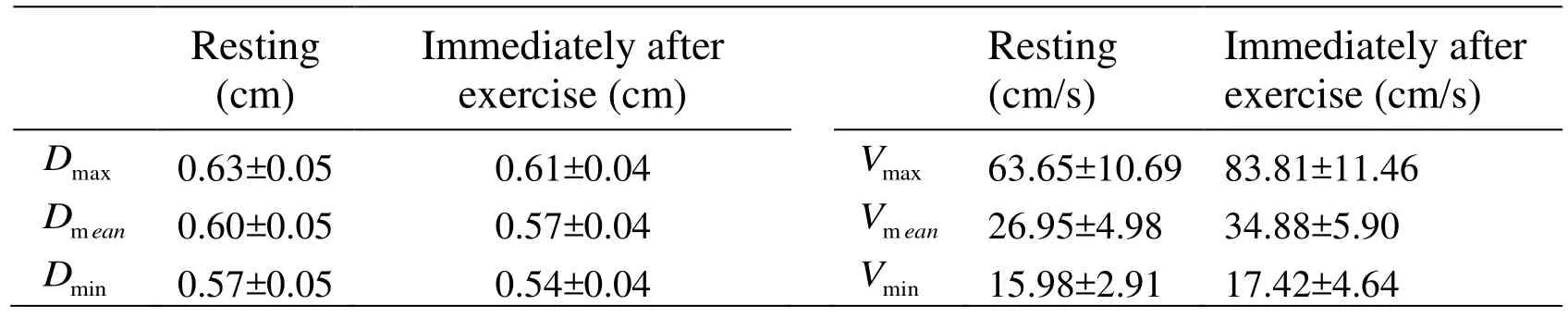
Table 1: Comparison of the arterial diameters (D) and center-line velocity (V) between resting and immediately after exercise

3.2 Effect of acute cycling exercise on the characteristic values of flow rates between the elastic and rigid tube models

As shown in Fig. 1c, the typical waveforms of flow rate based on both models are similar at the same states. More specifically, the comparisons of maximum, mean and minimum flow rates of twelve subjects calculated by the both models are demonstrated in Fig. 2.We can see that the maximum and mean flow rates immediately after exercise are markedly higher than those in resting state just as the typical waveforms (Fig. 1c) have shown. In addition, the minimum flow rate estimated by the rigid tube model exhibits significant decrease comparing to that estimated by the elastic tube model in resting state.Tab. 2 shows the numerical values of the maximum, mean, and minimum flow rates in resting state and immediately after exercise calculated by the both models, and the relative differences between the both models. It can be seen that the mean relative differences between the both models for the maximal and mean flow rates are below 4.5%, whereas the mean relative differences between the both models for the minimal flow rate in resting state and immediately after exercise reach 17.53% and 15.11%,respectively.

Figure 2: Flow rates in resting state and immediately after exercise (#p<0.05 Immediately after exercise vs. Resting, *p<0.05 Rigid tube model vs. Elastic tube model,n=12)

Table 2: Comparison of the flow rates calculated by the rigid and elastic tube model

3.3 Effect of acute cycling exercise on the characteristic values of WSS between the elastic and rigid tube models

Fig. 1d displays the typical WSS waveforms of a representative subject during one cardiac cycle based on the both models. It is observed that although the waveforms at same states are similar, the waveforms estimated by the elastic tube model move down compared to those for the rigid tube model.

According to Fig. 3, the maximum (Fig. 3a) and mean (Fig. 3b) WSS based on the both models are significantly elevated, and the minimum (Fig. 3c) WSS based on the both models are remarkably decreased immediately after exercise. Compared to the rigid tube model, there are significant reductions in maximum (Fig. 3a), mean (Fig. 3b), and minimum WSS (Fig. 3c) by the elastic tube model. Fig. 4a indicates that acute cycling exercise causes the increase of the OSI, but it is remarkable that this difference is significant only under the rigid tube model not in the elastic tube model. In addition, the exercise training remarkably increases the NEG and RRT under the both models (Figs. 4b and 4c). The elastic tube model significantly increases the OSI and RRT compared to the rigid tube model under both resting and immediately after exercise states (Figs. 4a and 4c), but the NEG is only raised in resting state (Fig. 4b).

Tab. 3 lists the numerical values of the maximum, mean, and minimum WSS, as well as the OSI, NEG, and RRT in resting state and immediately after exercise calculated by the rigid and elastic tube model, as well as the relative differences between the both models.It is clear to see that the mean relative differences of the maximum and mean WSS, and the RRT both in resting and immediately after exercise states are under 9.60%, but the mean relative differences of minimum WSS, OSI and NEG are as high as 28.90%,65.40% and 23.27% in resting state and 18.37%, 45.31%, and 14.30% immediately after exercise, respectively. Moreover, the mean relative differences of maximum and minimum WSS, OSI, and NEG in resting state are greater than those immediately after exercise. Although the mean relative differences of the mean WSS and the RRT in resting state are lesser than those in immediately after exercise, the differences are slight.

Figure 3: WSS in resting state and immediately after exercise based on the rigid and elastic tube model (#p<0.05 Immediately after exercise vs. Resting, *p<0.05 Rigid tube model vs. Elastic tube model, n=12).

Figure 4: The OSI (a), NEG (b) and RRT (c) in resting state and immediately after exercise based on the rigid elastic tube model (#p<0.05 Immediately after exercise vs.Resting, *p<0.05 Rigid tube model vs. Elastic tube model, n=12).

Table 3: Comparison of the WSS calculated between the rigid and elastic tube model

3.4 Effects of the variations of arterial diameter and flow rate on the WSS

It is concluded from Figs. 1, 2 and 3 that acute exercise induces the decrease in the arterial diameter and the increase in the mean flow rate, as well as the mean WSS. Both the decrease in the mean diameter and the increase in the mean flow rate will lead to the increase in the mean WSS. In order to establish the effects of variations in the arterial diameter and flow on the WSS following acute cycling exercise, the waveforms of the WSS versus the arterial diameter, as well as the waveforms of the WSS versus the flow rate are plotted in Fig. 5a and Fig. 5b, respectively. As shown in Fig. 5a, the WSS by the elastic tube model firstly increases and then decreases to negative values as the arterial diameter rises during systolic period, and it remains nearly constant during diastolic period except for a rapid increase at the early stage. In contrast, the WSS by the rigid tube model exhibits straight segments perpendicular to horizontal axis due to the constant arterial mean diameters. In addition, it is clearly seen that the WSS elevates as the flow rate increases during systolic period, and decreases as the flow rate reduces during diastolic deceleration period in both resting and post-exercise states. Notably, the results based on the elastic and rigid tube models exhibits analogous hysteretic behaviors. The relative change rates for the WSS, flow rate and arterial diameter following acute exercise are listed in the Tab. 4. It is observed that in the both models the mean relative variation rates of the maximum, mean and minimum flow rates are approximately 50% in the corresponding mean relative change rates of the maximum, mean and minimum WSS.

Figure 5: WSS versus arterial diameter (a) and WSS versus flow rate (b) during one cardiac cycle of a representative subject in resting state and immediately after exercise

Table 4: The relative variation rates (%) of the arterial diameter (D), flow rate (Q), and wall shear stress (WSS) before and immediately after exercise

4 Discussion

In order to estimate the pulsatile blood flow rate and the WSS in the common carotid artery, the arterial diameter and center-line velocity were measured with a color Doppler ultrasound, and the blood pressure was concurrently measured with an electronic sphygmomanometer first. The measured data demonstrate that the 30-min cycling exercise elicits remarkable increase in maximum and mean center-line velocity and mean blood pressure, but significant decrease in mean arterial diameter (data not shown), which are consistent with the experimental results from previous investigations of acute effect of cycling intervention on the common carotid hemodynamics by our group [Liu, Yuan, Qin et al. (2015)]. These increased values of the maximum and mean center-line velocity and mean blood pressure can be caused by the enhancement of cardiac contractility, while the decrease in the mean arterial diameter can be induced by the intensive contraction of blood vessel, which are predominantly attributed to the effect of increasing sympathetic nerve activity during exercise training [Simmons, Padilla, Young et al. (2011)].

The elastic tube model was adopted to calculate the waveforms and characteristic values of the blood flow rate and the WSS before and immediately after acute exercise;meanwhile, the rigid tube model was applied for a comparison. In our work, the blood viscosity and density for all subjects were respectively assumed to be the same standard values due to the normal body mass indexes (BMI, 22.93±1.94) and blood pressures(systolic pressure, 118.09±9.45, diastolic pressure, 72.82±5.23) of the healthy young subjects [Miles, Rees, Banerjee et al. (2008)]. In addition, Vandewalle et al. [Vandewalle,Lacombe, Lelievre et al. (1988)] demonstrated that one bout of 1-hour cycling exercise at 85% maximum heart rates caused the increase of blood viscosity by 6.8%. In the present study, the exercise intensity was one bout of 30 min cycling exercise about 60%maximum heart rates, which was less than half of the exercise intensity in Vandewalle’s study. If the increase of blood viscosity was assumed to be 3.4%, the increase of average WSS would be less than 3.4% (data not shown). Accordingly, considering the small changes of the WSS induced by blood viscosity, we neglected the effect of blood viscosity caused by the acute exercise, and considered the blood viscosities as the same in both states.

After calculation with the both models, we can see that the characteristic values of flow rate and WSS immediately after exercise make some changes. Firstly, the maximum and mean flow rates are enlarged (see Figs. 2a and 2b) immediately after the 30 min cycling exercise, which can promote more blood delivery to brain to ensure normal cerebellum movement regulation and nerve regulation [Iadecola, Li, Xu et al. (1996)]; meanwhile,rich oxygen supply induced by increased blood flow rate will enhance the brain function.Secondly, the exercise also induces significant increase in the maximum and mean WSS(see Figs. 3a and 3b), primarily ascribed to the aforementioned enhancements in the blood flow rate. Normally, the increased values of maximum and mean WSS are regarded as critical regulators to protect endothelium from the pathogenesis of atherosclerosis [Malek, Alper and Izumo (1999)].

The oscillating amplitude of the WSS waveform is also magnified immediately after exercise, including the increase in the anterograde and retrograde components of the WSS waveform (see Figs. 1d and 3). Retrograde shear stress has been generally perceived as contributing to atherosclerosis with the up-regulation of atheroprone genes,such as interleukin 8 (IL8), superoxide dismutase 2 (SOD2), vascular cell adhesion molecule 1 (VCAM1), angiopoietin-2 (ANGPT2), and so on [Malek, Alper and Izumo(1999); Amaya, Cancel and Tarbel (2016)]. Accordingly, the increased retrograde component of the WSS induced by exercises may enlarge these detrimental effects.However, the actual facts are that exercise training with the retrograde component of the WSS still improves the endothelial function [Hambrecht,Adams, Erbs et al. (2003);Green, Eijsvogels, Bouts et al. (2014)]. Moreover, Green et al. [Green,Bilsborough,Naylor et al. (2005)] also proposed that exercise-induced oscillatory WSS with anterograde and retrograde components promoted the generation of the vasodilator NO.Therefore, the importance of retrograde shear stress to endothelial function is indubitable no matter whether it is detrimental or beneficial. Certainly, further investigations are required to clear the air on the controversial topic of the detrimental or beneficial effects of the WSS with retrograde component, which is critical to identify the atheroprotective or proatherogenic effect of exercise-induced oscillatory WSS on artery endothelium.

It is clear from Figs. 1, 2 and 3 that the acute cycling exercise induces the decrease of mean arterial diameter and the increase of mean flow rate, which simultaneously contributes to the increase of mean WSS. As shown in Tab. 4, after acute exercise, the relative increased rates of the mean flow rate are around 19.86% by the elastic tube model and around 19.40% by the rigid tube model, respectively, which will be approximately contributing to the increase of the mean WSS around 19.86% and 19.40%according to the expression of the WSS in the artery under steady flow as follows[Potters, Marquering, VanBavel et al. (2014)]

where, Qmeanand Rmeanare the average flow rate and average radius of the common carotid artery, respectively. However, the WSS totally increases about 36.92% and 38.02% (Tab. 4), respectively, which demonstrates that the decreased mean diameter contributes to the increased mean WSS about 17.06% and 18.62%, respectively.Therefore, both the variations in the blood flow rate and diameter contribute almost equally in changing the value of the WSS.

The numerical results show that although the trends of the blood flow rates and the WSS profiles between the both models are very consistent (Figs. 1c and 1d). However, there are differences in the values between them (Figs. 2 and 3). Comparing to the rigid tube model, the minimum flow rate (Fig. 2c) and NEG (Fig. 4b) in resting state based on the elastic tube model are remarkably decreased and increased, respectively. Additionally,the maximum, mean, and minimum WSS in both states by the elastic tube model are more significantly decreased (Fig. 3), while the OSI and the RRT in both states are more markedly increased (Figs. 4a and 4c). More specifically, as shown in Tab. 2, the mean relative differences of the maximum and mean flow rates in two states are less than 4.50%, but the mean relative differences of minimum flow rates in two states are higher than 15.11%. In addition, as shown in Tab. 3, the mean relative differences of maximum and minimum WSS are less than 8.59%, but the mean relative differences of the minimum WSS and OSI exceed 18.37%. Thus, it can be seen that the vessel elastic deformation exerts greater effects on the minimum flow rate and the minimum WSS than their maximal values. Remarkably, the significant increase of OSI elicited by the exercise training occurs only in the rigid tube model instead of the elastic tube model. As described earlier, the retrograde components of the WSS, characterized by the OSI, had strong effects on endothelial biology towards a pro-atherosclerosis or anti-atherosclerosis phenotype [Amaya, Cancel and Tarbel (2016)]. Consequently, it is necessary to calculate the minimum WSS and the OSI with the elastic tube model accurately; otherwise, the false significant difference in OSI before and after exercise will exist.

Although the rigid tube model was proved as a good approximate approach to estimate the flow rates and the WSS [Schwarz, Duivenvoorden, Nederveen et al. (2015)], the effect of non-linear vessel elastic deformation was totally missing in this linear theory based on the rigid tube model. As it is clearly shown in the results of the rigid tube model that after taking the vessel elastic deformation into account, the minimum WSS are decreased and the OSI are raised in both conditions. Moreover, it is worth to note that the mean relative differences of the maximum and minimum WSS, the OSI, and the NEG with larger arterial vessel elastic deformation immediately after exercise are smaller than those with smaller arterial vessel elastic deformation in resting state. However, Qin and his co-workers [Qin and Jiang (2005)] pointed out that larger vessel elastic deformation would augment the relative differences of the minimum WSS and the OSI between both models. This discrepancy may result from the decreased mean arterial diameter by exercise (Fig. 1a) which was used in current numerical calculations while the mean arterial diameter was kept unchanged during numerical simulation studies by Qin and his co-workers [Qin and Jiang (2005)].

5 Conclusion

In this study, the elastic and rigid tube models were adopted to estimate the effect of acute cycling exercise on the pulsatile blood flow and the WSS, and to determine the roles of arterial diameter and flow rate in the change of WSS. It is found that the 30-minute cycling exercise induces significant increases in the maximum and mean values of the center-line velocity, flow rate and WSS, respectively, and it also causes remarkable decreases in the mean diameter and the minimum WSS. Although the trends of the WSS waveforms by the both models are consistent, the rigid tube model yields an overestimate of the WSS, mainly reflecting on the minimum WSS and OSI. Remarkably, the 30 min cycling exercise induces significant increase in the OSI by the rigid tube model but no significant change in the OSI by the elastic tube model. Accordingly, the consideration of vessel elastic deformation in assessing the effect of acute cycling exercise on the pulsatile blood flow rate and the WSS is a critical concern. In addition, the results also show that the arterial diameter and flow rate collectively contribute approximately equal changes in the mean WSS.

Acknowledgement:The research described in this paper was supported in part by the National Natural Science Foundation of China (Grant No. 31370948, 11672065).