穆苗苗, 马巧珍

(西北师范大学 数学与统计学院, 兰州 730070)

0 引 言

Plate方程源自弹性振动方程[1], 关于其解的整体存在性及渐近性的研究源于对弹性梁方程稳定性的研究[2]. 目前, 关于非线性耗散偏微分方程时间依赖吸引子的研究已得到广泛关注[3-6].

设Ω⊂n(n≥5)是具有光滑边界的有界区域. 本文考虑下列方程：

(1)

其中:u=u(x,t)为Ω×(τ,+∞)上的未知函数;α>0是阻尼系数;g∈L2(Ω);ε(t)∈C1()是有界的单调递减函数, 并满足

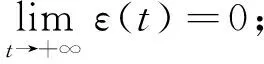
(2)

函数f∈C2(), f(0)=0, 且

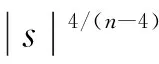
(3)

(4)

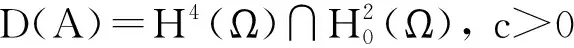
(5)

当ε(t)是一个与t无关的正常数时, 方程(1)已有许多结果[7-11]: 文献[7-8]给出了有界域上Plate方程一致吸引子的存在性; 文献[9-11]研究了Plate方程在无界区域上全局吸引子的存在性. 文献[12]给出了当ε(t)为依赖于时间t的函数时,Plate方程(1)时间依赖全局吸引子的存在性; 文献[13]运用压缩函数的方法证明了带有时间系数的非自治Plate方程时间依赖强拉回吸引子的存在性. 受文献[3,6,12]的启发, 本文在文献[12]的基础上, 进一步证明方程(1)中时间依赖吸引子的正则性和渐近结构.

1 预备知识

定义1(时间依赖全局吸引子)[3]过程U(t,τ)的时间依赖全局吸引子是最小的族U={At}, 满足下列条件:

1) 每个At在Xt上是紧的;

2) U是拉回吸引的, 即对每个有界族C={Ct}和每个固定的t∈, 均成立极限

记H=L2(Ω), 对应的内积与范数分别记为〈·,·〉,‖·‖. 对于0≤σ≤2, 定义由A生成的Hilbert空间族Hσ=dom(Aσ/4), 并赋予如下内积与范数:

〈w,v〉σ=〈Aσ/4w,Aσ/4v〉, ‖w‖σ=‖Aσ/4w‖.

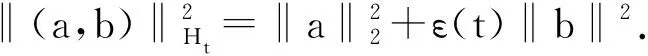
定义2[6]函数z: t→u(t)∈Xt是过程U(t,τ)的一个完全有界轨道(CBT), 当且仅当:

2) z(t)=U(t,τ)z(τ), ∀t≥τ, τ∈.

定理1[6]设U={At}是过程U(t,τ)的时间依赖全局吸引子, 若U是不变的, 则

At={z(t)∈Xt:z(t)是U(t,τ)的CBT}.

相应地, 有

U={z: t→u(t)|z(t)是U(t,τ)的CBT}.

设赋范空间Ht=X×Yt, 其范数为

∀(a,b)∈Ht,

其中: X是一个赋范空间; Yt是一族赋范空间.

记Πt: Ht→X为空间Ht关于第一个分量的投影, 即Πt(a,b)=a. 若Ft⊂Ht, 则ΠtFt={a∈X: (a,b)∈Ft}; 同理, 若F ={Ft}, 则记ΠF={ΠtFt}. 基于此, 假设过程U(t,τ)拥有不变的时间依赖全局吸引子U={At}, 则

ΠU={x:→X满足x=Πz, 且z是U(t,τ)的CBT}.

假设S(t): X→X(∀t≥τ)是作用在X上的半群, 存在全局吸引子A∞⊂X. 则由定义可知A∞⊂X是唯一的不变紧集, 即S(t)A∞=A∞(∀t≥τ), 且在X上依Hausdorff半距离吸引X上的有界子集.

引理1[6]如果

∀t≥τ,τ∈,

A∞={w(s):w是S(t)的CBT},

引理2[12]设式(2)～(4)成立, 则对任意的τ∈, 存在正常数c, 使得

(6)

定理2假设un是过程U(t,τ)的任一有界完全轨道序列, 则对任意tn→∞及任意s∈, 均存在S(t)的一个有界完全轨道w, 使得

‖un(s+tn)-w(s)‖X→0,n→∞,

(7)

则

(8)

定理3[12]设式(2)～(4)成立, 则问题(1)生成的过程族U(t,τ): Hτ→Ht在Ht中拥有不变的时间依赖全局吸引子At.

定理4[14]方程(5)对应的动力系统(H2,S(t))中拥有紧的全局吸引子A∞.

2 主要结果

2.1 时间依赖吸引子的渐近结构

下面讨论方程(1)对应过程U(t,τ)的时间依赖全局吸引子At与极限方程(5)的全局吸引子A∞之间的关系. 由文献[14]可知, 方程(5)可生成连续半群S(t): H2→H2, 且S(t)在空间H2中存在全局吸引子A∞, 并对任意的s∈, 有A∞={w(s): w是S(t)的CBT}.

引理3设式(2)～(4)成立, 则对过程U(t,τ)的任意完全有界轨道序列un及任意tn→∞, 存在S(t)的一个完全有界轨道w, 使得对每个T>0, 均成立

(9)

证明: 由引理2知, 对每个T>0, 序列{un}在空间

L∞(-T,T;H3)∩W2,2(-T,T;H1)

上是有界的. 根据文献[15]中推论4可知, 对任意的T>0, un(·+tn)在空间C([-T,T],H1)中是相对紧的. 因此存在函数w:→H2与un的子列(仍用un表示), 使得un(·+tn)→w(·), 且w∈C(,H2). 再结合式(6)知,

(10)

下面证明w是方程(5)的解. 令vn(t)=un(t+tn), εn(t)=ε(t+tn), 则关于un的方程(1)可记为

α∂tvn=-εn(t)∂ttvn-Δ2vn-f(vn)+g.

首先证明序列εn(t)∂ttvn在分布导数的意义下收敛到0. 事实上, 对每个固定的T>0及定义在[-T,T]上的光滑H-值函数φ, 均有

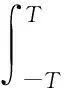
结合式(6), 可得

再由非线性项f(u)的增长性条件知, 对每个T>0, 在拓扑空间L∞(-T,T;H-2)中, 均有

-Δ2vn-f(vn)→ -Δ2w-f(w).

同时, 在分布导数的意义下有∂tvn(t)→wt(t), 因此可得

αwt+Δ2w+f(w)=g(x),

即w是方程(5)的解. 再结合式(10)知, w是半群S(t)的一个完全有界轨道.

定理5由定理3, 可得下列极限成立:

证明： 由定理3及引理3, 可得结论.

2.2 时间依赖吸引子的正则性

定义

ΠU={u:→H2, u=Πz, z为U(t,τ)的CBT}.

下面证明对任意的u∈ΠU, ‖ut‖2一致有界且其界与ε(t)无关.

定理6设式(2)～(4)成立, 则对某个C=C(U )>0, 成立

(11)

由于{uτ(τ),ut(τ)}∈Aτ, 因此

(12)

再结合式(6)与式(3)知

(13)

用2qt+2δq与式(11)在L2(Ω)中做内积, 可得

其中

利用Hölder与Young不等式, 估计

其中|ε(t)|≤L. 对足够小的δ, 有

(14)

再结合式(13)可得

根据上述估计可知, 对充分小的δ, 存在ν<δ, 使得

在[τ,t]上运用Gronwall引理, 并利用式(14), 可知对任意的t≥τ, 有

故结论成立.