Jincai Chen,Zhou Fang,Tong Qiu*

Department of Chemical Engineering,Tsinghua University,Beijing 100084,China

Keywords:Molecular reconstruction Structure oriented lumping Group contribution Monte Carlo Maximum information entropy

ABSTRACT Molecular management is a promising technology to face challenges in the refining industry,such as more stringent requirements for product oil and heavier crude oil,and to maximize the value of every molecule in petroleum fractions.To achieve molecular management in refining processes,a novel model that is based on structure oriented lumping(SOL)and group contribution(GC)methods was proposed in this study.SOL method was applied to describe a petroleum fraction with structural increments,and GC method aimed to estimate molecular properties.The latter was achieved by associating rules between SOL structural increments and GC structures.A three-step reconstruction algorithm was developed to build a representative set of molecules from partial analytical data.First,structural distribution parameters were optimized with several properties.Then,a molecular library was created by using the optimized parameters.In the final step,maximum information entropy(MIE)method was applied to obtain a molecular fraction.Two industrial samples were used to validate the method,and the simulation results of the feedstock properties agreed well with the experimental data.

1.Introduction

The refining industry today has to comply with higher product-quality specifications,more stringent environmental regulations and heavier crude oil.To address these issues,a promising technology that is termed molecular management,which targets the right molecules to be in the right place,at the right time and at the right price,has been of increasing interest.To achieve molecular management,the feedstock composition should be known with great detail.However,no analytical technique is yet sufficiently effective to detect and quantify the thousands of different compounds in the heavy petroleum fraction.Consequently,it is necessary to reconstruct a mixture from partial analytical data.Several approaches have been described in the literature to represent the petroleum fraction.

Quann and Jaffe[1,2]proposed a method that is termed structure oriented lumping(SOL)in which they attempted to use a group of structure vectors to describe complex hydrocarbon molecules.Because a structure vector represents a class of molecules with the same functional groups but with different structures,the number of complex hydrocarbons has been reduced from millions to thousands,and the model complexity has been reduced.Jaffe[3]extended this method to heavy petroleum residues and more specifically to a representation of multicore species.This method has been used widely in the oil industry and has received great feedback.However,it is still a challenge to estimate the properties of molecules that are described by structure vectors.

Zhang[4]used a matrix of pseudo compounds that are classified by chemical family and carbon number to characterize the petroleum fraction.There are several other approaches using variations of matrix representations with homologous series[5,6].This method can keep much valid information of the feedstock.However,long and complex analyses are needed to obtain this matrix,and it is difficult to apply the method to heavy petroleum residues.

Neurock et al.[7]proposed a method that is termed stochastic reconstruction(SR),which characterizes the petroleum fraction by a set of distributions of molecular structural attributes.Monte Carlo(MC)sampling is used in this method,which makes it possible to provide a large ensemble of computational molecules with properties that are close to experimental values.With rapid developments in computer science,MC method can play a greater role in molecular reconstruction.Hudebine et al.[8,9]developed a two-step algorithm for molecular reconstruction to rebuild light cycle oil from overall petroleum analyses.The first step was based on SR,and the second step used an approach that is termed maximum information entropy(MIE)method.The results showed a reasonably good agreement with industrial data.MIE has become an effective tool for optimization problems,although it requires a particularly well-defined initial set of molecules.

In this work,we propose a novel molecular reconstruction model based on SOL and GC methods,combined with MC method to create a molecular library and MIE method to determine the molecular fraction.The first part of this paper provides an introduction to SOL method.SOL structural increments are associated with GC structures to estimate the normal boiling point(NBP)of organic compounds and for further research.The second part presents a three-step reconstruction algorithm.First,structural distribution parameters are optimized with several properties.Then a molecular library that contains thousands of different molecules is built to characterize the feedstock.In the third step,MIE method is used to obtain the molecular fraction.The last part focuses on the application of the novel method to two different feedstocks in order to assess the versatility of this new method.

2.SOL and GC Methods with Their Associating Rules

In SOL method,a molecular type is subdivided into some basic structural increments.Every structural increment is a specific combination of C,H,S,N and O atoms that exist in the feedstock.As shown in Table 1,there are twenty-one structural increments in total which are appropriate for describing heavy petroleum fractions,with the structure vector Z and stoichiometric matrix G[10].Every molecule can be described by a vector,whereas not all vectors can represent reasonable molecules in the feedstock.As a consequence,the numbers of structural increments is subjected to a limited range,which aims to ensure that every constructed molecule falls within the heavy petroleum fraction.The ranges are summarized in Table 2.

A mixture that represents feedstocks can be constructed by structure vectors,but it is still a challenge to estimate the mixture properties.Molecular elemental compositions and molecular mass can be computed easily from the contributions of the increments' elemental stoichiometry.The overall C,H,S,N and O contents of any molecule are simply the product of the G matrix and its structure vector Z:

Average molecular mass also can be calculated from the C,H,S,N and O content.By identifying which group of four constituents(saturates,aromatics,resins and asphaltenes;SARA)every molecule belongs to,the SARA property can be calculated based on the molecular mass.However,it is difficult to acquire the properties of simulated distillation,in which molecules are sorted according to their boiling points.Therefore,it is necessary to estimate the NBP of every molecule.

GC method is a simple and accurate way to estimate properties of organic compounds,which is widely used in the oil industry.In this method,the prediction of properties is based exclusively on the molecular structure,which is performed by summing the number of occurrences of each group in the molecule times its corresponding contribution.In 1987,Joback[11]proposed a simple way which only considered a small quantity of structures.Gani et al.[12,13]improved GC method by adding more structures,and divided them into first to third-order groups.

To predict the NBP of molecules that are described by structure vectors,structural increments in SOL method need to be associatedwith structures in GC method.In this work,the GC method proposed by Marrero and Gani[13]was used as a basis,and only structures in the first-order groups were considered.All the group contribution data of the first-order groups are from this method as well.Twentyone SOL structural increments have been divided into three types:fundamental,attached and substitutional structural increments.Fundamental structural increments can exist independently,whereas attached structural increments need to be attached with fundamental structural increments.Substitutional structural increments would change the state of atoms in fundamental and attached structural increments.It is necessary to consider different conditions to calculate the group contribution of these structural increments.Some examples are provided.The structural increment A6 contains six a CH in first-order groups,so the group contribution of A6 is simply six times that of a CH.However,some structural increments are more complex to be associated with structures in first-order groups,and some can have different values under different conditions.As for A4,when it is attached to A6,it contains four a CH,and changes two a CH in A6 to two aC.When it isattached to AS,it contains four a CH,and change one CH=CH(cyclic)in AS to two a C.As for AA,when it exists between two aromatic rings,it changes two a CH to a C.Two other situations are also considered.Calculation details of the examples are shown in Table 3.The group contributions of all structural increments for calculating NBPs and their descriptions are given in Table 4.

Table 2 Value ranges of the structural increments

Table 1 Structure vector Z and stoichiometric matrix G in SOL method

Table 3 Calculation details of three examples

Table 4 Description of structural increments and their group contribution

The equation which is used to estimate the NBP is the same as thatin the GC method proposed by Marrero and Gani[13],where Tbis the estimated value of the NBP;i is the number of structural increments;Niand Tb1iare the number and group contribution of structural increment i,respectively.

Several examples,including heteroatom-contain molecules,are given in Tables 5 to 8.For example,Table 5 shows the estimation of the NBP of Anthracene by using the Eq.(2),and the error is−6.21 K,which is acceptable.

In this work,only the property of NBP has been estimated by the associating rules between SOL structural increments and GC structures.In fact,more properties can also be estimated,such as critical properties,density and standard enthalpy of formation.With the associating rules,it is easy to achieve the group contribution of structural increments for other properties.Therefore,this work can also play a role in further reaction studies.Moreover,the structures in GC method are more detailed,so molecules can be described more concretely by GC structures.Thus,by associating the two methods,rough molecular description can be improved,and molecules can be described by specific structure.In the study of many downstream chemical processes,actual molecules with specific structures are necessary.Therefore,this work can also contribute to the connection between the models of oil upstream refinery processes and downstream chemical processes.

3.The Three-step Molecular Reconstruction Algorithm

3.1.Optimizing structural distribution parameters

Because heavy petroleum fractions contain a large number of molecules,probability sampling of the MC method can be applied to create molecules.In this work,19 structural increments except IH and AA were sampled and assembled according to a χ2distribution function.IH and AA can be calculated from the numbers of other structuralincrements.The probability density function oftheχ2distribution function is shown as follow:

Table 5 Estimation of the NBP of Anthracene(experimental value:613.2 K)

Table 6 Estimation of the NBP of dibenzothiophene(experimental value:605.6 K)

Table 7 Estimation of the NBP of quinoline(experimental value:511.2 K)

Table 8 Estimation of the NBP of phenylacetic acid(experimental value:538.7 K)

where Γ(α)is the gamma function:

When Eq.(5)is established,

sampling can be achieved by using the following equation:

where x is the value of every sampling;xmin,xmaxis the minimum and maximum of the structure;r is the expectation of x;μ is the parameter inχ2distribution and RN is a random number that obeys a uniform distribution in[0,Q].

To ensure that the molecules fall within the heavy petroleum fraction,the parameter r in the distribution function of every structural increment should be optimized.The objective is minimizing the difference between calculated and experimental properties.In this step,only properties that describe the distribution proportion such as elemental compositions and SARA need to be considered.The model can be written as follow:

where ELE are the elemental compositions;SARA is the four constituents(saturates,aromatics,resins and asphaltenes)in the heavy petroleum fraction;e and c represent experimental and calculated values respectively.The constraint is that the parameters of all the structures' distribution functions are positive.

This problem can be solved by simulated annealing algorithm coded in Matlab language.In 1983,kirkpatrick et al.[14]created an intelligent optimization algorithm that is termed the simulated annealing algorithm which can achieve a globally optimal solution.To decrease the computer memory requirements and simulation time,and to satisfy the accuracy,1000 molecules were sampled.In this step,the optimized structural distribution parameters can be obtained.

3.2.Creation of molecular library

By using the optimized structural distribution parameters,a large molecular library can be created.In this work,20000 molecules were sampled by MC sampling.However,many molecules were created twice or more.Thus,every molecular structure vector needs to be checked to ensure that every molecule is counted only once in the molecular library.Moreover,the sampled molecules will be judged by their NBP in real time to ensure that only the qualified molecules will be recorded and pass to subsequent procedures.Through the step,several thousand qualified molecules were created in the molecular library for the heavy petroleum fraction.

3.3.Optimizing mole fractions of molecules

In 1948,Shannon[15]proposed the concept of Shannon's information entropy,which is defined as follow:

where S represents Shannon's entropy and πiis the probability of a certain state.

When Shannon's entropy reaches its maximum,the most rational state is achieved.By replacing the probabilities in Eq.(8)by mole fractions of the molecules and by maximizing the information entropy,optimum mole fractions can be achieved,which means the most likely composition of the computational molecules based on maximum information entropy theory.Thus,a closer matching between the mixture properties of the set of molecules and those of the petroleum fraction can be obtained.After replacing the probabilities πiby the mole fractions ziof the molecules in Eq.(8),the objective can be rewritten as follow:

with the constraints:

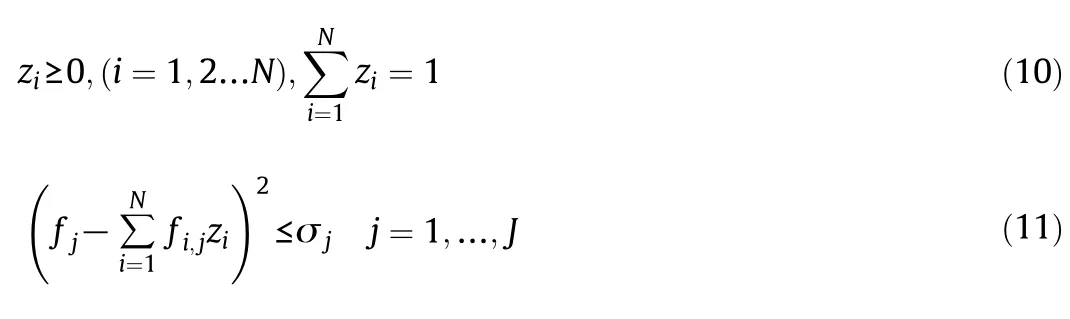
where fjis the value of constraint condition j;fi,jis the coefficient of constraint condition j to molecule i;N is the sampling size(the number of molecules in the library);J is the number of constraints and σjis the uncertainty of constraint j.

This model can be solved by the penalty function which has been applied extensively to calculate the optimal value with constraints.In this method,a new function that incorporates the function F(z,c)and its constraint g(z)is as follows:

where parameter c is a constant variable and is termed the penalty factor.This problem can also be solved by simulated annealing algorithm.The overall simulation steps are summarized in Fig.1.

4.Application to VGOs

The new method was applied to two different vacuum gas oils(VGOs).VGO is a petroleum fraction that is drawn from the side line of a vacuum distillation column.This petroleum fraction is an extremely complex mixture that contains thousands of different species,which are only analyzed roughly.Thus,only partial analytical data can be used in molecular reconstruction.The two samples of VGO that were used in this work are shown in Table 9.

Table 10 shows the results from optimizing structural distribution parameters.Because these parameters are the mean values in the χ2distribution,they can stand for the number of structural increments in a molecule.Therefore,it is understandable that except from R,br and me,structural distribution parameters of all the other structural increments are quite small,around or less than one.By using the optimized parameters,20000 molecules were created in each case,and 3460 unique molecules remained finally in the molecular library to describe VGO No.1 after all the molecules had been identified and qualified whereas 3411 molecules were used to describe VGO No.2.

Fig.1.Simulation diagram of VGO.

Tables 11 and 12 show the results from properties after optimizing mole fractions of the molecules.The relative errors between experimental and calculated data for all the calculated properties were below 7%.Because errors have already emerged during estimating NBP of the molecules,it is unnecessary to pursue a high accuracy in the final step.Compared with the previous work[16],more properties and a much larger molecule library have been considered,thus a more accurate representation of VGO is achieved at the molecular level.Compared withthe traditional two-steps approach[17],the structural distribution parameters were optimized with several properties,and molecules in the molecule library were checked,so that the molecule library is more likely to have molecules in the actual feedstocks.

Table 9 Properties of the VGOs

Table 10 Optimized structural distribution parameters

Table 11 Comparison of experimental and calculated results of VGO No.1

Table 12 Comparison of experimental and calculated results of VGO No.2

5.Conclusions

This work built associating rules between SOL structural increments and GC structures.On the one hand,the associating rules develop a new way to estimate the NBP of molecules described by structure vector.Thus,the property of simulated distillation can be used as a constraint in reconstruction to achieve a molecular result that is closer to the real feedstock.On the other hand,the associating rules offer a new idea to estimate other properties and to demonstrate the possibility of integrating models of upstream oil refinery processes and downstream chemical processes.

A novel three-step reconstruction algorithm was proposed,combined with MC and MIE methods.This new method was successfully applied to the molecular reconstruction of VGO for hydrocracking.Two types of VGO were simulated by this combined method and the properties of average molecular mass,elemental compositions,SARA and simulated distillation were calculated.The relative errors between calculated and experimental data for all the calculated properties were below 7%.