丛伟杰, 何 磊

(西安邮电大学 理学院， 陕西 西安 710121)

一类分类马氏椭球学习机的目标是将样本数据中的目标类和非目标类区分开[1-2]，是数据挖掘[3-4]中的一个重要问题。一类分类马氏椭球学习机在图像识别[5]，遥感成像[6]，工程故障检测[7-8]等技术领域有着广泛实际应用。

解决一类分类问题最常用的方法是基于支持向量域描述[9](Support Vector Domain Description，SVDD)的马氏椭球学习机[10](Mahalanobis Ellipsoidal Learning Machine，MELM)，其核心思想是用马氏距离代替SVDD中的欧氏距离，这样就可以考虑到样本点的分布信息，从而得到更加紧致的超椭球边界，以替代原来的超球边界，使样本分类的准确率得到提高。但是，在训练样本点较少情况下，这种方法的分类准确率并不高。其主要原因MELM通过训练样本所构造的判别函数，必须对所有待分类样本点进行判别。当训练样本点较少时，所构造的判别函数分类性能较差。为此，将支持向量机中的直推模式[11]学习方法引入到MELM中，从而得到直推式马氏椭球学习机[12](Transductive Mahalanobis Ellipsoidal Learning Machine，TMELM)。 该方法在训练过程中，不断将待分类样本点通过逐渐学习方式加入到训练集中，使构造函数不断得到优化，即使在训练样本点较少情况下，分类准确率明显提高。但是，TMELM方法在迭代时，选取加入到新训练集中的待分类样本点，遍及当前所形成的超椭球内部的全部待分类样本点。这样就会使得在重新训练时，因数据集规模过大而造成运行时间较长、系统效率不高的问题，尤其是在处理较大规模数据集时，该问题就变得更加明显。

为了在保证较高准确率的前提下，提高运算效率，本文采用有效处理最小闭包球问题[13]的割平面法思想和基于协方差的初始化策略，提出了一种改进的直推式马氏椭球学习机(Improved Transductive Mahalanobis Ellipsoidal Learning Machine，ITMELM)。ITMELM在迭代过程中，仅仅选取距离当前超椭球中心最远的待分类样本点，加入到新的训练集中进行重新训练，以提高计算效率。在ITMELM中，使用基于样本协方差矩阵构造的初始化策略[14]来提高较大规模数据集上最小体积超椭球的计算效率。通过对比实验验证ITMELM的分类准确率和计算效率。

1 马氏椭球学习机算法概述

1.1 预备知识

设X表示n×M样本矩阵，包含M个样本xi∈n(i=1,2,…M)，在SVDD中使用加入样本信息的马氏距离代替欧氏距离，得到可以包含近乎全部训练样本点的超椭球[10]

E(a,R)={x∈n:
(x-a)TΣ-1(x-a)≤R2}，

其中，a是得到的超椭球的球心，R为超椭球的半径。离群点是超椭球外侧的点，在上述过程中需要求解下面的规划问题

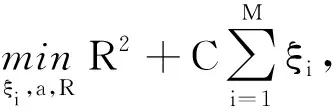
(1)

式中，ξi≥0是对应允许存在在超椭球外侧样本点的松弛变量，C是用来均衡在椭球内外侧的样本点的数量和得到超椭球的规模的参数，Σ是样本点的协方差矩阵。从而可以获得式(1)的Lagrangian对偶问题

(2)

式中αi和αj为相应样本点对应的拉格朗日乘子。设

k(xi,xj)=φ(xi)Tφ(xj)，

φ(xi)与φ(xj)分别为xi与xj在空间中的映射，利用中心化核矩阵[10]

KC=QTΩQ，

其中

Q=[(1/M)(I-(1/M)E)]1/2，
Ω=QKQ，K=k(X,XT)，

I为M×M单位矩阵，E是M×M全1矩阵。可得到该问题的核形式为

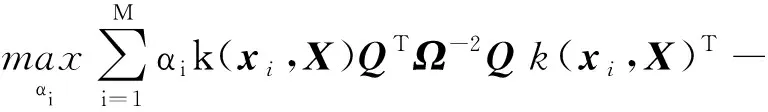
(3)

显然，式(3)是一个二次凸优化问题。

下面，将利用式(3)构造对未知类别的待分类样本的判别函数。特征空间中的样本点到球心a的马氏距离的平方为

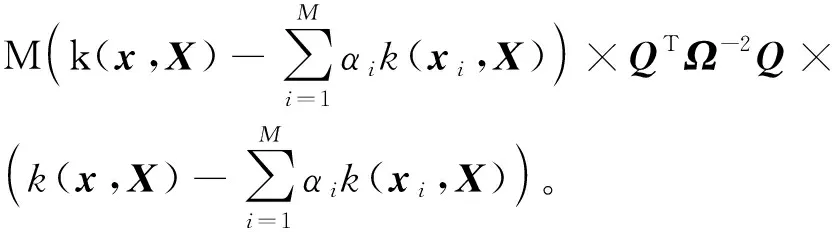
(4)

如果一个未知类别的待分类样本点满足条件

d2(φ(x),a)≤R2,

(5)

则这个样本点就被认为是属于目标集所在的类，否则就会被认为是非目标集所在的类。

1.2 MELM算法

马氏椭球学习机[10]是处理判别函数一种常用算法，具体步骤可描述如下。

1)给定参数C1和C2，通过对已知类别的样本点进行训练学习获得最初的超椭球E0(a0,R0)，这个过程即是求解式(3)的问题过程；

2)利用所得到的超椭球，并利用式(5)对未知类别的样本点进行分类；

3)当所有待分类样本点判别完成后，输出相应结果，MELM算法结束。

可以看出，MELM算法是通过对已知类别的训练样本点进行初始化，获得一个最初的超椭球并结合离群点的判定条件，然后，对未知类别的待分类样本点进行判定。

1.3 TMELM算法

直推式马氏椭球学习机[12]是为了提高马氏椭球学习机的分类准确率的一种改进算法，算法具体步骤如下。

1)给定参数C1和C2，初始迭代p=0时，对已知类别样本点进行训练学习，获得最初的超椭球E0(a0,R0)，利用式(5)对未知类别的样本点进行初次分类；

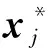
Einterior(a,R)={x∈n:
(x-a)TΣ-1(x-a)≤R2+ξi,ξi=0};

3)使用步骤2中所得到的超椭球Ep+1(ap+1,Rp+1)，对其余未知类别的待分类样本点进行判断，直到将所有未知类别的待分类样本点判别完成。如果未判别完成，则跳转到步骤2；

4)当所有待分类样本点判别完成后，输出相应结果，算法TMELM结束。

算法TMELM基于MELM算法并引入支持向量机中直推式的思想[12]进行改进，即通过已知类别的训练样本点获得一个最初的超椭球，利用目标点的判定条件对未知类别的样本点进行初次判定，将符合条件的样本点加入到原有的训练集中，同原有的训练集一起组成一个新的训练集，并对其进行重新训练，从而可以得到一个相对上一次迭代性能更加优化的超椭球。不断迭代上述过程，直到所有未知类别的待分类样本点全部判别为止。但其在处理较大规模数据集时，就会出现算法耗时较长的问题。

2 改进的直推式马氏椭球学习机

为了改善TMELM算法在处理较大规模数据集时耗时较长的问题，提出一种改进的直推式马氏椭球学习机算法(ITMELM)。

首先，对已知类别的训练样本点进行初始化，并在初始化过程中引入样本协方差初始化策略思想[14-15]。把每次迭代后组成的已知类别训练样本作为下一次需要进行初始化的样本点，令

其中X∈n×M表示为一个列向量矩阵，该矩阵是由已知类别的训练样本中的样本点组成，e∈M是分量均为1的列向量。矩阵Q(e)可表示为[15]

Q(e)=M2(e)。

样本点到超椭球中心的距离为

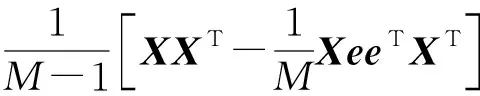
类似于文献[14]，在所有初始化已知类别的训练样本点中，选择距离当前中心最远的前2n个对应的样本点，记为A0={xi1,xi2,…,xi2n}。这时，得出初始的可行解为u0∈M，将u0输出，其中可行解u0的分量为或∉A0。

考虑到需要对待分类样本点能够作出较好的判别分类，并且得到一个更精确的类描述。因此，需要求解以下的优化问题[10]

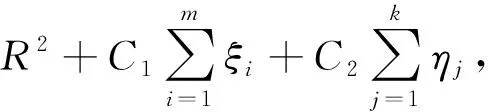
(6)

式中x1,x2,…,xm∈n为一组已知的训练样本点，y1,y2,…,yk∈n为待分类样本点，C1和C2是给定的参数，分别表示已知和未知类别的训练样本点的影响因子。为保证所得到参数的可靠性，通常通过十倍交叉校验的方法获得。

改进算法的训练过程也是求解式(6)优化问题的过程，而对未知类别待分类样本点的判别则要求其要满足式(5)的条件。

用类似于直推式支持向量机启发式算法[16]的思想，ITMELM算法的具体步骤如下。

1)给定参数C1和C2，当迭代次数p=0时对已知类别的样本点使用样本协方差初始化策略进行训练，并获得超椭球E0(a0,R0)，利用式(5)对未知类别的待分类样本点进行分类；

2)如果第p(p≥1)次迭代对应的样本点yj满足yj∈Einterior(ap,Rp)，则计算所有符合条件的yj及当前迭代所形成的超椭球中心点的距离，选取距离最大的点(一个或多个点)，并将这些点加入到训练样本中，和原有的训练样本组成新的训练集，重新训练后得到下一次迭代的超椭球Ep+1(ap+1,Rp+1)；

3)使用步骤2中得到的超椭球Ep+1(ap+1,Rp+1)对其余未知类别的待分类样本点进行判断，直到将所有未知类别的待分类样本点判别完成。如果未判别完成，则跳转到步骤2；

4)当所有待分类样本点判别结束后，输出相应结果，算法ITMELM结束。

ITMELM算法首先使用样本协方差的初始化策略对所有的已知类别的训练样本点进行初始化，进而会得到一个初始的超椭球，其次结合目标点的判定条件对未知类别的待分类样本点进行初次判定，最后在所有符合条件的样本点当中选取距离当前超椭球中心点最远的样本点，并将它们加入到原有的目标点集当中形成新的训练样本点集，通过重新训练得到一个新的超椭球，再使用它去判定剩余的待分类样本点。

其中使用样本协方差初始化策略可以得到更好的初始超椭球，而在下一次迭代过程当中使用这种策略得到的超椭球的判别准确率也会稍好一些。在加入目标点的过程中通过使用处理最小闭包球问题的割平面法思想选择的样本点更有意义，因为在形成超椭球的过程中，越靠近边界的点与其他部分的点相比较，它们可以更快地形成满足条件的超椭球，减少整个算法的迭代次数，进而缩短了需要的运行时间。这样将待分类样本的信息通过逐渐学习的方式加入到改进算法中的训练样本集合中，使判别模型每通过一次训练学习都会提高其原有模型的判别准确率，经过多次的不断学习后可以达到一个比较满意的结果。因此ITMELM算法与MELM算法和TMELM算法这两种算法相比，可以在确保较高分类准确率的前提下，有效地减少算法运行时间，从而更好地提高处理较大规模数据集的计算效率。

3 实验结果与分析

为了验证本文ITMELM算法的效果，在实际数据上，将本文ITMELM算法与MELM算法[10]和TMELM算法[12]分别进行对比试验。实验运行的环境为MatlabR2014a。实验过程中使用的实际数据集是从University of California Irvine(UCI)机器学习数据库[17]中进行选取的。实验数据不仅选取了文献[12]中的5组数据进行对比试验，还选取了5组较大规模的数据进行验证ITMELM算法相较于TMLEM算法的计算效率。在进行实验前，对所选取的数据集先需要做一些简单处理，如去掉了少量不完整数据，在数据内部调整数据位置信息等；对于多种类别的数据集，则选取其中一种类别为所要学习的类别，并选取该数据集中约22%的数据作为初始训练数据，剩余数据作为待分类数据，其目的是为了保证在训练样本中样本点比较少，而待分类样本点比较多的情况下进行对比试验。

实验过程中采用径向基核函数为

并通过十倍交叉验证的方法选择核参数σ及参数C1，C2，以期选取最优结果的平均值。

表1为实验所选数据的特征描述。表2分别给出了三种算法在相同数据集上执行所得准确率和运行时间的实验结果。从表2中可以看出，在已知类别的训练样本点较少而未知类别的待分类样本较多的情况下，MELM算法的判别准确率比TMELM算法和ITMELM算法均明显较差。这是因为MELM算法在通过使用已知类别的训练样本得到初始超椭球后，然后对未知待分类样本进行判别，因初始训练样本数量较少，故得到的判别类型准确率自然不高。而对于TMELM算法和ITMELM算法，均使用了增量学习的策略，在得到初始超椭球后，再对待分类样本点判别时，不断将待分类样本点信息加入到学习机中进行重新训练，从而逐渐改善了模型的判别准确率。对比ITMELM算法和TMELM算法的分类准确率结果也可以看出，ITMELM算法可以达到与TMELM算法的相当高的分类准确率。这是因为ITMELM算法在初始化时加入样本协方差初始化策略，将得到一个相较于TMELM算法更优的初始超椭球，所以，其分类准确率相对于TMELM算法在部分数据上会略有提高。

另外，从表2中还可以发现，MELM算法相对其他两种算法的运行时间最少，但是它的分类准确率较低，从综合性能角度来看，MELM算法相对较差。对比ITMELM算法和TMELM算法的运行时间结果很容易发现，ITMELM算法的运行时间会较小，且ITMELM算法的运行时间比TMELM算法至少可以减少24.9% 以上。其原因是在增量学习过程中，加入了样本点构成新的训练集时，TMELM算法是将每次迭代中的全部的样本点均加入到新的样本集合中，而ITMELM算法每次均选取距离超椭球中心点距离最远的点加入到训练样本中，由于这些样本点相对于其他样本点来说，可以更快地形成超椭球，从而避免了在迭代过程中重复寻找超椭球的过程，同时，这样的点作为支持向量点，可以更加快速地形成预期的超椭球，减少了加入全部点时形成超椭球的迭代次数，进而使整体运行时间缩短。

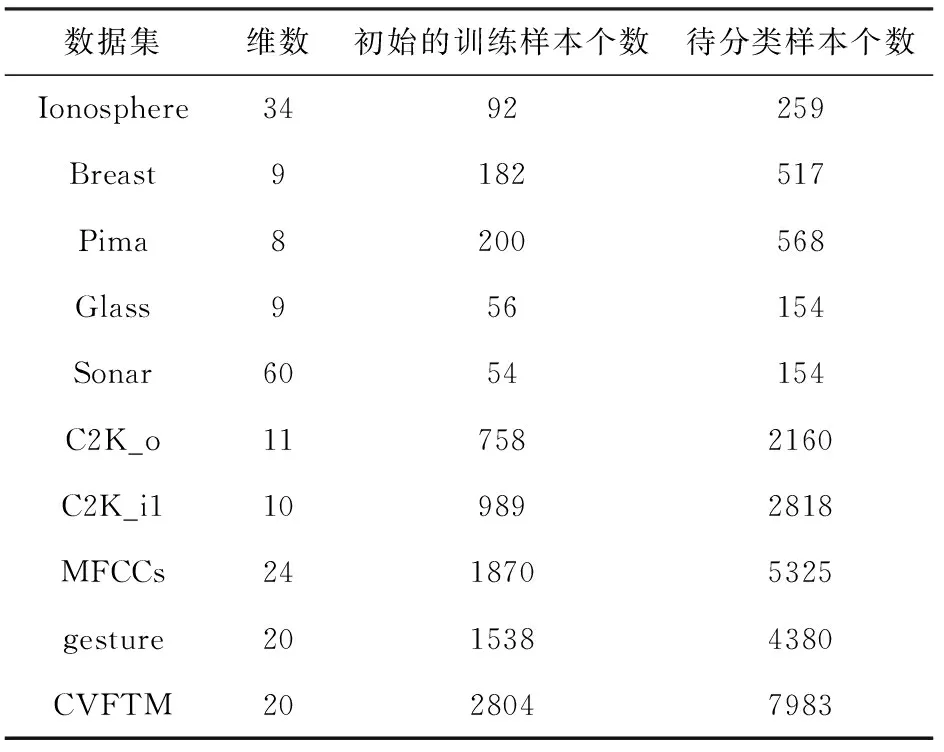
表1 实验数据特征

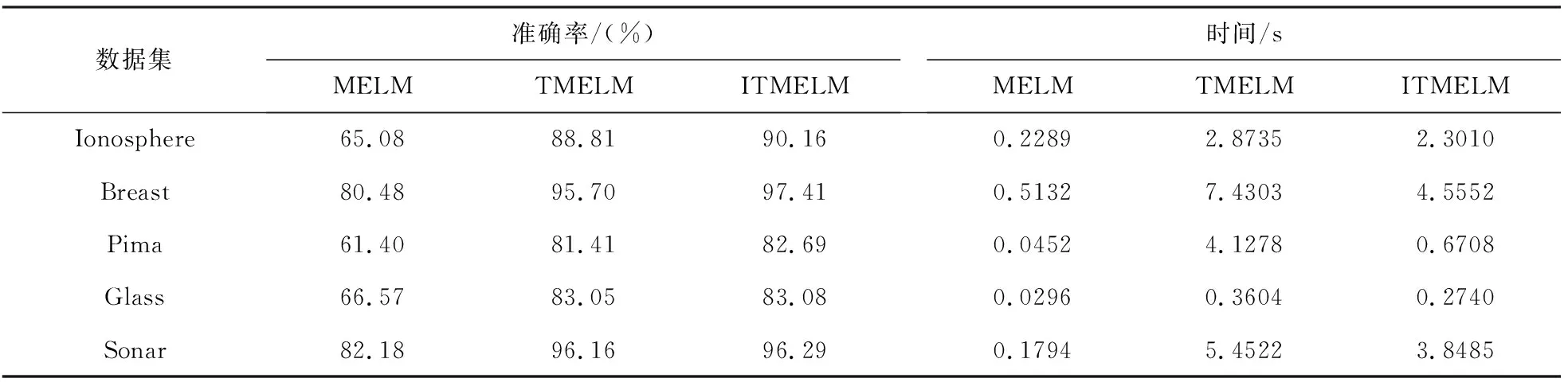
表2 3种算法的准确率和运行时间

在较大规模数据集下,3种算法的准确率和运行时间如表3所示。从表中可以看出，在数据规模较大的情况下，ITMELM算法的分类准确率可以与TMELM算法相当，但是，ITMELM算法运行时间进一步降低，ITMELM算法的运行时间比TMELM算法缩短了约2～5倍。主要原因在于采用了样本协方差初始化策略，对于规模比较大的数据集，相对于较小规模数据集情形，运算的迭代次数减少地更加明显。因此改进算法在处理大规模数据时更具有优势。

表3 三种算法在较大规模数据下的准确率和运行时间结果

4 结论

针对在训练样本点较少的情况下，马氏距离进行直推式一类分类椭球学习机处理较大规模数据集时间较长的问题，提出了一种改进的直推式马氏椭球学习机算法(ITMELM)。一方面，ITMELM有效地使用样本协方差的初始化策略进行初始化过程；另一方面，采用将离超椭球中心点最远的待分类样本点加入到训练样本点中的方式，并循序渐进的作出判别分类，具有较强的自我学习能力。实验结果和分析表明，在保证较高分类准确率的前提下，相对于MELM算法和TMELM算法， 本文所提ITMELM算法能有效地减少运行时间。特别是在较大规模的数据且训练样本较少的情况下，将能保证较高分类准确率同时，还能极大地缩短处理数据的运行时间。因此，本文提出的ITMELM算法，在处理训练样本比较少、待分类样本较多的规模较大数据时，是一个可供选择的有效算法。