云南 马孟华

高三数学应如何复习备考，才能有效地提升备考效率，提升学生的思维水平，一直以来都是一线教师研究和实践的重要课题.本文结合自身的课堂教学实践，从数学课堂上常见的“一题多解”模式入手，抛开单纯的解题过程，从对高考试题由浅入深、多维度视角的剖析中体现出试题蕴含的数学思想方法，站在体现数学思想方法的高度领略和感悟试题.从多种解法中提炼数学思想方法，再从数学思想方法的引领中优化解题思路，两者相辅相成，共同提升备考效率和思维水平.

在高考复习备考中，如果老师能适当地、有意识地选择设计一些学生力所能及的典型问题进行一题多解，不仅会使学生提升对知识系统的横向联系和深刻理解，也可以开拓智力、培养和训练学生的发散思维能力、优化解题思路，最终在不同的解法思路下带领学生领略和掌握数学思想方法这个强大的数学武器，最终达到通过解决一个问题来领悟多种数学思想方法，从而提升高考复习备考的效率，让学生真正从思想武器的角度解决数学问题.

本文从2017年全国新课标卷Ⅲ理科12题的多维度分析入手，阐述了不同解法下蕴含的不同数学思想方法，并从中总结出解决高中阶段最值、范围问题的常用、有效的方法.

下面我们来看看2017年全国新课标卷Ⅲ理科12题.

( )

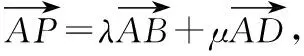
分析本题以向量知识为背景，考查最值问题，涉及代数、三角、解析几何等内容，涉及知识面较广.纵观高考数学中最值问题的求解方法主要以双变元消元法、三角换元法、数形结合法以及不等式放缩法为主，故可结合课堂教学实际，通过多方位、多层次的思考对本题采用一题多解的教学模式，在展示解题思路和方法的过程中带领学生领悟数学思想，掌握求解最值问题的多种手段，提升复习备考效率.

解如图所示，以点A为原点，AD方向为x轴正方向，AB方向为y轴正方向建立xAy坐标系，

故可得到以下各点的坐标：

A(0,0),B(0,1),C(2,1),D(2,0).

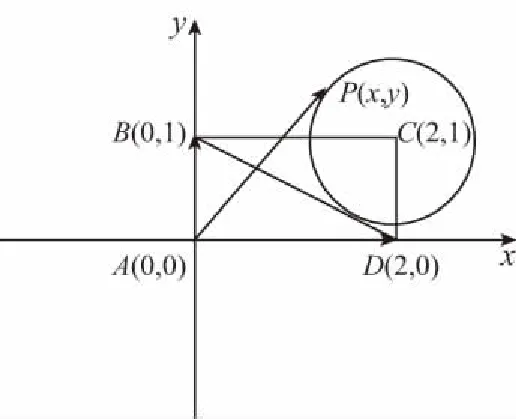
圆C与BD相切，则点C到BD的距离即为圆C的半径r，由等面积法：

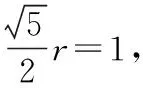
处理向量与圆综合的问题，一般情况下会利用几何和代数方法求解，结合题意，本题中的矩形条件就是题眼，自然想到了建立平面直角坐标系，转化为代数方法求解.顺利建立坐标系，将几何问题转化成代数问题.

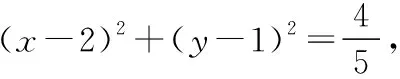
设动点P的坐标为(x,y)，

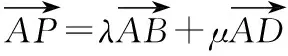
结合要求λ+μ的最大值，

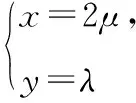
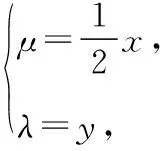
策略1双变元消元法(函数思想)

双变元消元法的核心在于将两个变量控制的函数经过消元转化为一元函数，其前提条件是需知晓两个变量之间的等式关系，最终将二元函数的最值问题转化为一元函数的最值问题.

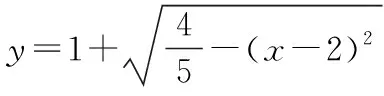
此时，z是变量x的一元函数，而求该函数的最大值也需采用换元法，

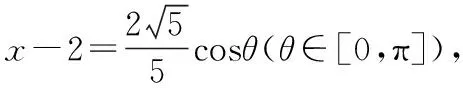
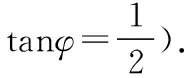
故此时可得λ+μ的最大值为3.

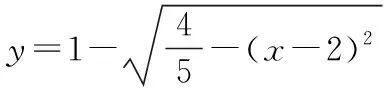
由于θ∈[0,π]，φ为锐角，故z=-sin(θ-φ)+2<3,

综上,λ+μ的最大值为3.

评注此法应用了函数与方程思想，将双变元函数通过消元法转化为一元函数求最值，最后利用换元法求解一元函数最值，过程还需要分类讨论，是比较复杂的一种解题方式.由于其复杂性和难操作性易被教师和学生所忽视.但笔者认为函数思想其实是求解此类问题中的一种通法，应该引起教师和学生的重视.一直以来，高考对数学思想方法的考查注重从学科整体意义和思想价值的高度立意，有明确的考查目的，加强针对性，注重通性通法，淡化特殊技巧，力图有效地检测考试对数学知识中所蕴含的数学思想方法的掌握程度.此法既强调了解决最值问题的一般处理模式，同时又在无形中拓宽和提升了学生解决一元函数最值问题的能力，对于高三课堂复习教学来说，既强调了对通式通法的掌握，又拓宽了研究数学问题的思路和方向，有效地提升了复习备考效率和学生的思维水平，让学生能够带着数学思想和方法举一反三，以不变应万变.

策略2判别式法(方程思想)

策略3三角换元法/参数方程法(转化和化归思想)

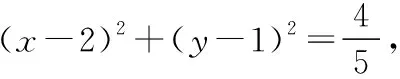
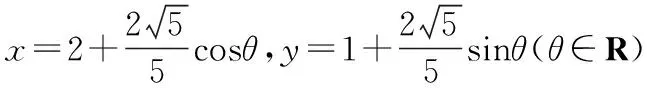
则(*)式转化为

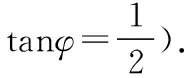
故此时可得λ+μ的最大值为3.

评注此法实则采用了化归和转化的思想，通过将条件转化为参数方程形式，使问题柳暗花明，相较于函数思想，此法优势明显.化归和转化的思想是高考中必考的数学思想方法，其核心是将未知解法或难以解决的问题，通过观察、分析、联想、类比等思维过程，选择恰当的方法进行变换，化归为在已知知识范围内已经解决或容易解决的问题.该解法中，巧妙地将圆方程改写为参数方程，将结果表达成了学生熟知的三角函数形式，故最值问题迎刃而解.

下面再来看看在转化和化归思想引导下的另一种解题策略.

策略4数形结合法(数形结合思想)

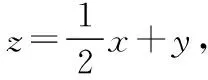
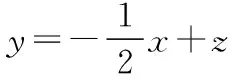
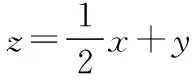
对待数学问题，学生不仅要善于对题目的表面形式进行观察并发现其特点，而且也要善于挖掘条件和转化其结论，把未知的条件或待求的结论化归为已知条件或已知结论，综合利用函数方程思想、转化和化归思想、数形结合思想解决问题.下面我们来看看本题的变式探究.

变式探究

在数形结合方法下，本题中求解λ+μ的最大值可改编成为：

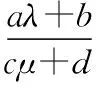
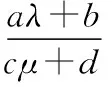
变式2求λ2+4μ2+aλ+bμ+c(其中a,b,c为常数)的最值.

解法：将λ2+4μ2+aλ+bμ+c化简如下：

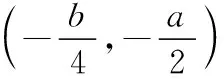
在数学习题教学复习备考中，恰当的采用变式整合复习的教学手段，以基本问题为载体，通过再生问题进行变式教学，以题根为基准对一定幅度的知识进行扫描教学，也是一种高效、有效的提升复习备考效率的手段，同时也是加强和巩固对数学思想方法理解和应用的重要手段.

策略5不等式放缩法(分类与整合思想)

在前4种策略背景下，观察到条件为变量x,y的二次方程，而结论却是变量x,y的一次表达式，故可联想到是否可以利用柯西不等式求解？下面来看看思维过程.

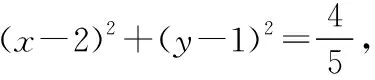
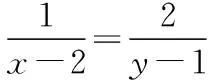
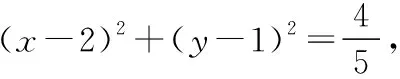
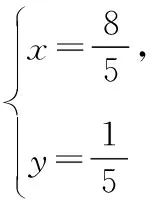
综上,λ+μ的最大值为3.

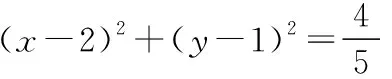
小结本例从多角度对试题进行剖析，并在不同的解题策略中感悟和理解了不同数学思想方法的应用，收获不小.以上五种策略的阐述在高三复习备考中不仅有效培养学生对数学思想方法的理解和掌握，而且也给出了高考中必考点：最值、范围问题的常用处理方法(即“函数法”“判别式法”“换元法”“数形结合法”“不等式法”)，可谓一举两得，极大地提高了高考复习备考的效率，让学生更有学习的欲望和动力，并提升了对数学学习、高考备考的信心.

下面我们再来看看高考数学和竞赛数学试题中对最值、范围问题的考查中所蕴含的数学思想方法.

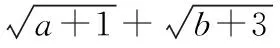
解法一(双变元消元法，函数思想)

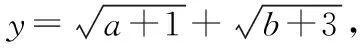
解法二(不等式放缩法，分类和整合思想)

方向1构造柯西不等式求解

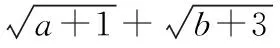
方向2构造重要不等式求解

由于a+b=5，故(a+1)+(b+3)=9，

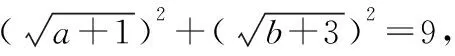
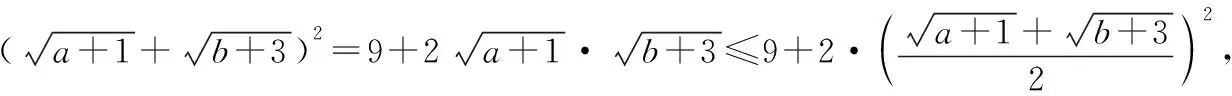
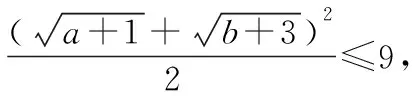
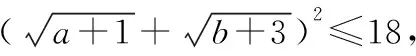
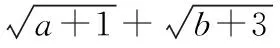
当然，该方法利用配凑的方式得到结论的整体表达式，技巧性较强，学生难于接受和理解.这里我们还是比较偏向于使用柯西不等式法，方法简洁明快，效果显著.

解法三(代数换元法，数学结合思想、转化与化归思想)

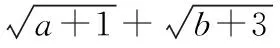
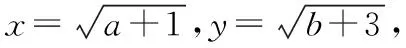
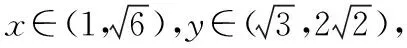
方向1(数形结合法，数形结合思想)

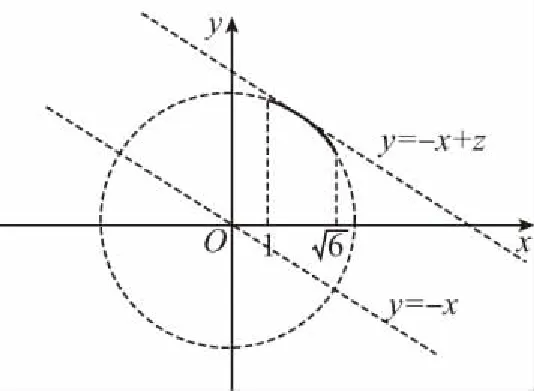
方向2(三角换元法，转化与化归思想)

令x=3cosθ,y=3sinθ，

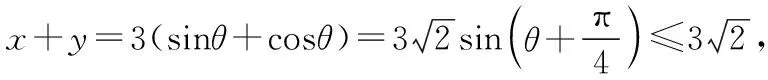
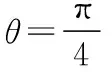
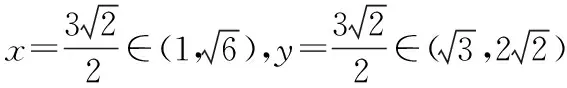
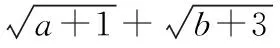
解法四(判别式法，方程思想)

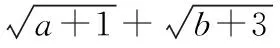
再如：

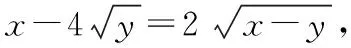
分析从实数x,y满足的等式关系来看，分离出x，并将等式关系化简为x=f(y)的形式是极其困难且难以实现的.

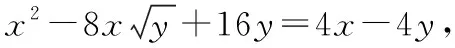
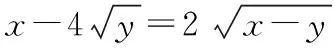
解法一(函数与方程思想)

对方程两边平方，

方程变为20t2-8xt+x2-4x=0(t≥0)，

故方程20t2-8xt+x2-4x=0有非负实数解，

所以x的取值范围为{0}∪[4,20].

解法二(换元法，数形结合思想、分类与整合思想)

在思路2的基础上，问题转化为已知a,b满足方程(a-1)2+(b-2)2=5(a,b≥0)，求a2+b2的取值范围.

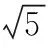
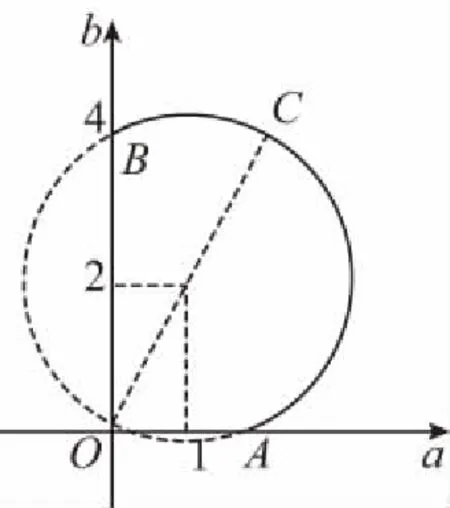
当动点(a,b)和定点O(0,0)重合时，动点到定点间的距离为0；

当然，全国数学联赛试题难度较大，不宜放到高三复习课上进行讲解.但从高考复习备考的角度，若将本题的结论改编为“求x的最大值”，则问题的难度就降低了，这样就比较适合对高三学生的训练和提升了.经过改编后，本例不仅能够从多维度提升学生的思维水平，而且也能加强学生对最值问题求解思路的深刻理解.在改编模式下，除了以上两种解法外，还可以考虑不等式放缩法求最值，方法如下：

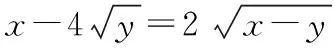
注意到右边可利用柯西不等式进行放缩，即

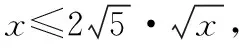
“一题连数点，多解显本质”.“数点”就是多种解题策略，而本质就是数学思想方法.高考对引导数学教学起着重要作用，要提高解题的能力和水平，首先应该站在较高的观点上去研究解题，从数学的本质上看待解题，在解题的过程中体现数学思想方法，在思想方法的引领下不断创新解题思路.最终以不变应万变，才是我们数学高考备考以及日常教学所追求的.