周水生, 姚 丹

(西安电子科技大学 数学与统计学院, 西安 710126)

支持向量机(support vector machines, SVM)[1]的主要思想是最大限度地分开两类训练样本. 由于SVM能较好地克服维数灾难等问题, 因而在模式分类、回归分析、文本分类和生物信息学等领域应用广泛[2-4]. 为了研究交叉分类问题, Jayadeva等[5]提出了非平行平面的分类器, 即孪生支持向量机(twin support vector machines, TWSVM), 其基本思想是构造两个非平行的超平面进行分类, 其中每个超平面拟合一类样本且尽量远离另一类样本. TWSVM将传统的一个规模较大的凸二次规划问题转化为两个规模较小的凸二次规划问题, 提高了训练速度[6]. 邵元海等[7]在TWSVM的基础上提出了孪生边界支持向量机(twin bound support vector machines, TBSVM), 其通过在目标函数上增加正则化项实现结构风险最小化. 目前, 对TWSVM的改进已有许多[8-9], 使得TWSVM在鲁棒性和泛化性能等方面均有提高. Kumar等[10]提出了最小二乘孪生支持向量机(least squares twin support vector machines, LSTSVM), 与LSSVM的不同点在于求解过程变成了求解两个等式方程组, 因而提高了求解效率, 减少了存储空间. 基于LSTSVM, 陈静等[11]提出了加权的最小二乘孪生支持向量机(weighted least squares twin support vector machines, WLSTSVM), 其通过对样本增加权重, 提高该算法的鲁棒性, 但WLSTSVM分类效果的好坏取决于权重的选择, 从而制约了其应用范围.

当样本数据规模较大时, 文献[10,12-13]给出的LSTSVM算法需要训练样本较多, 使模型出现求逆过程计算量大、易产生过拟合、训练速度慢、计算复杂度高等缺点. 针对LSTSVM算法的不足, 本文基于Sherman-Morrison定理[14]和迭代算法提出一种改进的最小二乘孪生支持向量机(based on Sherman-Morrison theorem and iterative algorithm an improved least squares twin support vector machine, SMI-ILSTSVM)增量学习算法, 对最小二乘孪生支持向量机进行改进和优化.

1 最小二乘孪生支持向量机

LSTSVM的基本思想是通过构造两个超平面进行分类, 每个超平面回归一类样本且尽量远离另一类样本[5]. 线性的LSTSVM就是求解下述问题：

LSTSVM1：

(1)

LSTSVM2：

(2)

其中: A表示正类样本; B表示负类样本;c1,c2表示惩罚参数; e1和e2表示全一向量. 根据式(1),(2), 可求得线性LSTSVM的解为

(3)

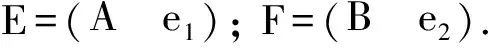
(4)

最后, 可使用所得到的超平面(4), 并应用判别函数, 即

(5)

非线性情况通过构造核函数的方法获得, 非线性的LSTSVM为

(6)

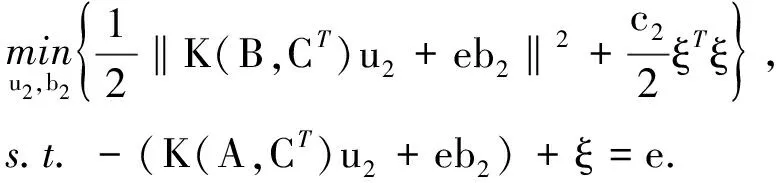
(7)

根据式(6),(7), 可求得非线性LSTSVM的解为

(8)

(9)

(10)

2 改进的最小二乘孪生支持向量机

由于LSTSVM的求解难度在于求解规模为(m+1)×(m+1)矩阵的逆, 如果该矩阵为非满秩矩阵, 则求解结果会出现病态解的现象[6]. 文献[13,15]都是基于经验风险最小化原则对LSTSVM进行不同的改进, 所以本文提出一种改进的最小二乘孪生支持向量机(improved least squares twin support vector machine, ILSTSVM).

2.1 线性ILSTSVM

在线性LSTSVM的目标问题上加入经验风险最小化原则, 得到下述问题：

ILSTSVM1：

(11)

ILSTSVM2：

(12)

可以求出式(11),(12)的解, 即

(13)

2.2 非线性ILSTSVM

对于非线性的情况, 采用核函数的方法, 即

类似于线性ILSTSVM的求解方法, 可求出式(14),(15)的解, 即

(16)

3 SMI-ILSTSVM增量学习算法

3.1 矩阵求逆分解定理

本文提出的SMI-ILSTSVM算法, 主要采用对矩阵的逆进行分解, 然后重组矩阵的逆, 最终得到一种结构相对简单、计算量较小的迭代求解算法, 其原理是通过迭代求解利用前一次的计算结果求逆, 不必直接求大样本矩阵的逆.

定理1(Sherman-Morrison定理)[14]若矩阵A是一个可逆矩阵, u和v均为向量, 且

1+vTA-1u≠0,

则当u=v时,

(17)

3.2 线性SMI-ILSTSVM增量学习算法

增量学习(incremental learning)[16]算法降低了对时间和空间的需求, 更能满足实际要求, 但每次迭代过程中只增加一个样本, 会导致计算效率偏低. 本文采用随机法选择训练样本, 在一定程度上降低了增量学习算法对分类精度的影响, 且每次随机选择一列训练样本也提高了计算效率.

(18)

所以对于扩展矩阵E计算更新后的ETE, 仅添加了一个小矩阵ssT, 更新后SMI-ILSTSVM模型的解可写为

(19)

由于式(19)中存在单位矩阵, 所以式(19)总是非奇异的, 此时可利用式(17)分解矩阵的逆. 令

(20)

则v1=-M-1FTe2, v2=N-1ETe1. 进一步计算可得

根据上述推导过程, 线性SMI-ILSTSVM增量学习算法如下.

算法1线性SMI-ILSTSVM增量学习算法.

输入: 训练集{X,L}, 罚参数ci>0(i=1,2,3,4);

1) (n,m)=size(X);

3) fori=1∶ndo

s=(Si)T和l=Li;

4) ifi==1 then

5) else

7) end if

8) end for.

观察线性ILSTSVM的解式(13), 可知该模型的复杂度为O(((m+1)3+(m+1)2)n), 而线性SMI-ILSTSVM增量学习算法的复杂度为O(2(m+1)2n), 降低了复杂度, 因此, SMI-ILSTSVM增量学习算法计算效率更高.

3.3 非线性SMI-ILSTSVM增量学习算法

非线性SMI-ILSTSVM的扩展向量为

由于非线性情形下计算高斯核矩阵需花费大量的时间和内存, 因此可先随机选取样本C的子集Z, 用核矩阵K(A,ZT)代替K(A,CT), 使SMI-ILSTSVM算法在训练时仅使用部分样本数据, 不但减少了算法的总计算量, 且降低了存储空间, 在不影响分类性能的基础上, 使算法具有稀疏性.

衡量稀疏性的一个指标----稀疏水平[17]的计算公式为

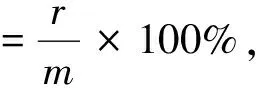
(22)

其中:r为训练样本中非零解数量的比例;m为训练样本的大小. 先令

(23)

则

v1=-P-1HTe2, v2=Q-1GTe1.

进一步计算可得

其中:

根据上述推导过程, 非线性SMI-ILSTSVM增量学习算法如下.

算法2非线性SMI-ILSTSVM增量学习算法.

输入: 训练集{X,L}, 罚参数ci>0(i=1,2,3,4), 高斯核函数参数σ∈(2-11,23);

1) (n,m)=size(X);

3) fori=1∶ndo

4) ifi==1 then

5) else

7) end if

8) end for.

4 实验结果与分析

为了评价SMI-ILSTSVM算法的性能, 下面进行人工数据和UCI数据集的仿真实验. 实验条件为： Windows7系统, 8 GB内存, Intel(R)Core(TM)i7-4790 CPU@3.6 GHz, MATLAB R2014a, 核函数为

4.1 人工生成数据实验

先随机生成200个交叉型样本点, 其中左类和右类各100个, 分别用SVM和TWSVM构造分类面. 实验结果表明, TWSVM的精度约为90%, 而线性SVM的精度约为60%. 对于交叉型数据集, TWSVM的分类效果比SVM的分类效果好. LSTSVM,WLSTSVM和SMI-ILSTSVM三种分类器针对含有噪声的交叉样本集的分类结果如图1所示.

图1 3种分类器的分类结果Fig.1 Classification results of three classifiers

由图1可见, LSTSVM和WLSTSVM分类器在交叉样本点上受噪声影响较大, 这是因为文献[11]提出的权重算法对于交叉数据集缺乏鲁棒性, 而本文提出的SMI-ILSTSVM增量学习算法的分类效果较好.

4.2 UCI数据集的实验结果

为了验证SMI-ILSTSVM增量学习算法的分类性能, 本文选取列于表1中的6个标准UCI数据集, 并分别对线性和非线性两种类型的SMI-ILSTSVM,WLSTSVM,LSTSVM,TWSVM进行分类精度与训练时间的仿真实验. 在实验中, 线性情形采用线性核函数, 非线性情形采用高斯核函数, 训练集随机选取原有训练集的30%进行训练, 核参数在区间[2-11,23]内选取, 惩罚参数ci>0(i=1,2,3,4)在区间[0,2]内选取, 所有参数的选取方法均采用十折交叉验证法[7,10]. 4种方法得到的分类结果列于表2～表5.

表1 标准UCI数据集属性

表1可见, 本文提出的线性SMI-ILSTSVM增量学习算法对于6种UCI数据集的分类精度和训练时间均好于TWSVM,LSTSVM和WLSTSVM. 对于同一个数据集, SMI-ILSTSVM的分类精度基本上最高, WLSTSVM的分类精度次之, 而TWSVM和LSTSVM的分类精度差别不大； SMI-ILSTSVM的训练时间最少, TWSVM的训练时间最多.

表2 线性核情形下4种方法的分类精度比较

表3 线性核情形下4种方法的训练时间比较

表4 非线性核情形下4种方法的分类精度比较

表5 非线性核情形下4种方法的训练时间比较

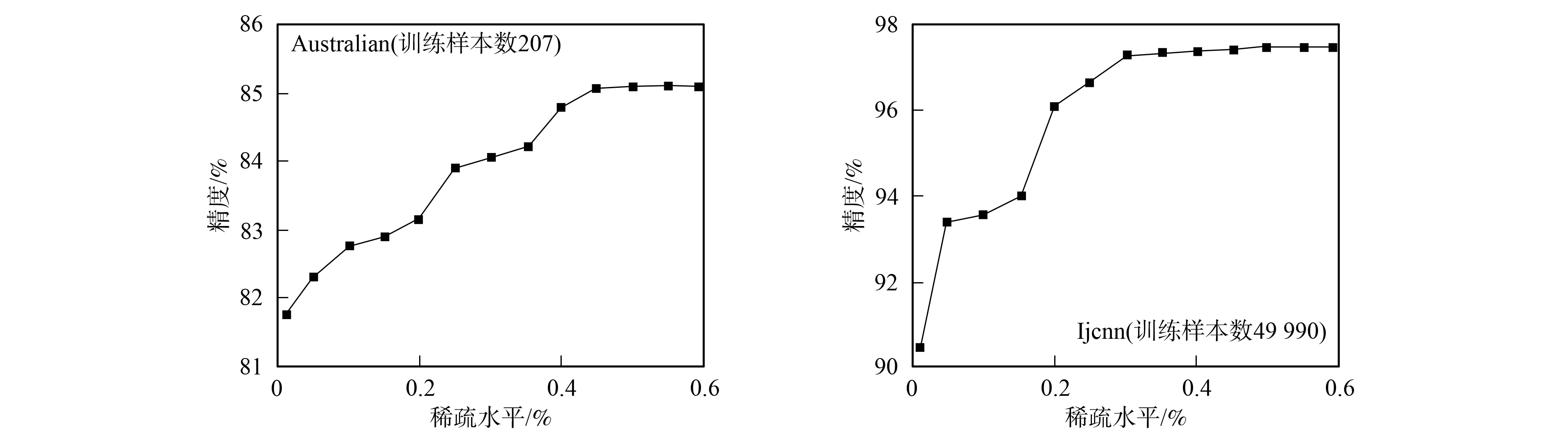
图2 大规模数据集的稀疏水平Fig.2 Sparse level of large scale datasets

由表2～表5可见, 本文提出的非线性SMI-ILSTSVM增量学习算法对于6种UCI数据集的分类精度和训练时间均好于TWSVM,LSTSVM和WLSTSVM. 对于同一个数据集, SMI-ILSTSVM的训练时间最少, 这是由于随机选取训练样本的子集进行训练, 可确保较少的训练时间, 但牺牲了一定的分类精度； WLSTSVM的训练时间最多, 是由于计算样本权重提高分类精度比较耗时, 所以其分类精度较高. 因为非线性SMI-ILSTSVM增量学习算法在训练时仅使用部分样本数据, 所以在UCI数据集上并非一致地优于其他3种已有算法, 这也是本文算法有待进一步提高之处. 本文算法的优势在于不仅降低了存储空间, 而且减少了算法的总计算量, 使算法具有稀疏性. 稀疏性是解向量的非零元素个数, 本文使用其相对值, 即稀疏水平. 利用式(22)计算出不同训练样本对应的稀疏水平如图2所示. 由图2可见, 本文提出的非线性SMI-ILSTSVM增量学习算法对于大规模数据集均具有一定的稀疏水平.

综上可见, 本文提出的SMI-ILSTSVM增量学习算法较LSTSVM算法具有更好的泛化性能, 避免了在求解该目标函数时对病态矩阵求逆的处理, 算法的分类精度和训练时间有明显提高； 采用随机选择法选取训练样本的一列, 在一定程度上降低了增量学习算法对分类精度的影响, 也提高了计算效率； 引入随机选择训练样本的一个子集代替全部训练样本, 使核函数的计算量减小, 从而使算法具有稀疏性, 减少了运算时间. 在UCI数据集上的实验表明, 本文算法能实现高精度和高效率的分类效果, 且适用于含有噪声的交叉样本集分类.