孟旭东, 王三华

(1. 南昌航空大学科技学院 思政与基础教学部, 南昌 330034； 2. 南昌大学 理学院, 南昌 330031)

含参解集映射的连续性为研究集值优化问题的稳定性、对偶性、适定性、连通性等奠定了基础. Zhao[1]给出了含参规划问题解集映射下半连续性的最优性条件; Klatte[2]在比Slater条件更弱的假设下, 讨论了含参凸规划问题解集映射下半连续性的充分性条件; Chen等[3]借助标量化的技巧, 讨论了含参广义向量均衡问题解集的连续性. 目前, 关于含参向量平衡问题解集的半连续性, 特别是下半连续性的研究已有很多结果[4-6]. 集值优化问题分析一般包括向量优化准则和集优化准则[7]两种方案. 运用向量优化准则方案讨论含参单值优化问题与含参集值优化问题解映射的连续性类似, 所以运用向量优化准则讨论含参集值优化问题解映射连续性的意义有限. 基于两种准则, 目前, 已有集值优化问题解映射的存在性结果[8-9]、最优性条件[10-11]、适定性理论[12-13]及对偶性理论[14-15]等研究成果. 文献[16]给出了含参集值优化问题解集映射连续的最优性条件. 受文献[16]启发, 本文通过引入双参广义集值优化问题, 给出集值映射l-严格锥-拟凸的概念, 并讨论解集映射的上、下半连续性及闭性的最优性条件.

1 预备知识

设X,Y,Z为拓扑向量空间, Ω,Λ⊂Z为非空子集, 记P0(Y)为Y所有子集的全体,K⊂Y为闭凸尖锥. 借助文献[9,11]的记号, 设A,B∈P0(Y), 用≤l与≪l分别表示P0(Y)上的如下关系：

A≤lB⟺B⊂A+K,A≪lB⟺B⊂A+intK.

易知如下定义的集关系～l为P0(Y)上的等价关系：

A～lB⟺A≤lB,B≤lA,

记P0(Y)上的等价关系类～l的全体为[·]l.

定义1[17]设S⊂P0(Y), 如果对任何B∈S,B≤lA, 均有A≤lB, 则称A∈S为集S的l-最小集. 记S的所有l-最小集的全体为l-minS.

注1若A∈S为集S的l-最小集, 且B∈S满足B∈[A]l, 则B为集S的l-最小集.

设M⊂X为非空子集,F:M→2Y为给定的集值映射, 广义集值优化问题(l-SOP)定义如下：

定义Θ∶={F(x):x∈M}.

定义2[17]设x0∈M, 称x0为问题l-SOP的l-最小解当且仅当F(x0)∈l-minΘ.

对每个(λ,μ)∈Λ×Ω, 考虑含参广义集值优化问题(Pl-SOP)：

定义3[18]设H:Ω→2X为给定集值映射,μ0∈Ω给定, 则：

1) 称H在μ0处下半连续当且仅当对任何开集V⊂X, 均满足V∩H(μ0)≠Ø, 且存在μ0的邻域N(μ0), 使得对任何μ∈N(μ0), 都有V∩H(μ)≠Ø；

2) 称H在μ0处上半连续当且仅当对任何开集V⊂X, 均满足H(μ0)⊂V, 且存在μ0的邻域N(μ0), 使得对任何μ∈N(μ0), 都有H(μ)⊂V；

3) 称H在μ0处为闭的当且仅当对每个网(μn,xn)∈graphH∶={(μ,x):x∈H(μ)}, (μn,xn)→(μ0,x0), 均有(μ0,x0)∈graphH；

4)H在Ω上下半连续(上半连续)当且仅当H在每个μ0∈Ω处下半连续(上半连续),H在Ω上连续当且仅当H在Ω上既上半连续又下半连续.

由文献[18-19]知, 定义3中集值映射H在点μ0∈Ω处上(下)半连续.

命题1[18-19]设H:Ω→2X为给定集值映射,μ0∈Ω给定, 则：

1)H在μ0处下半连续当且仅当对任何序列{μn}⊂Ω,μn→μ0及任何x0∈H(μ0), 均存在xn∈H(μn), 使得xn→x0；

2) 若H为紧值的(即对每个μ0∈Ω,H(μ0)为紧集), 则H在μ0处上半连续当且仅当对任何序列{μn}⊂Ω,μn→μ0及任何xn∈H(μn), 均存在x0∈H(μ0)及子列{xnk}⊂{xn}, 使得xnk→x0.

设M:Ω→2X,F:X×Λ×Ω→2Y为给定集值映射, 定义集值映射LF(y,λ,μ):X×Λ×Ω→2X为

LF(y,λ,μ)={x∈M(μ):F(y,λ,μ)≤lF(x,λ,μ)}={x∈M(μ):F(x,λ,μ)⊂F(y,λ,μ)+K}.

记LF的定义域为DLF, 其中DLF={(y,λ,μ)∈X×Λ×Ω:LF(y,λ,μ)≠Ø}.

定义4设M:Ω→2X为凸集值映射,F:X×Λ×Ω→2Y为集值映射, (λ0,μ0)∈Λ×Ω给定, 若对任何x0,x1,x2∈M(μ0),x1≠x2及t∈(0,1), 均满足F(x0,λ0,μ0)≤lF(x1,λ0,μ0)且F(x0,λ0,μ0)≤lF(x2,λ0,μ0), 使得F(x0,λ0,μ0)≪lF(tx1+(1-t)x2,λ0,μ0), 即F(tx1+(1-t)x2,λ0,μ0)⊂F(x0,λ0,μ0)+intK. 则称F(·,λ0,μ0)在M(μ0)上关于(λ0,μ0)为l-严格K-拟凸的.

注2若F:X×Λ×Ω→Y为向量单值映射, 则F(·,λ0,μ0)在M(μ0)上关于(λ0,μ0)为l-严格K-拟凸的, 即为文献[20]中一类经典的向量单值函数的严格K-拟凸.

2 问题Pl-SOP解集映射的连续性

设(λ0,μ0)∈Λ×Ω给定. 假设:

(H1)M(·)在μ0处具有紧值且上半连续；

(H2)M(·)在μ0处具有紧凸值且连续；

(H3)F(·,·,·)在M(μ0)×{λ0}×{μ0}上具有紧值且连续;

(H4)F(·,λ0,μ0)在M(μ0)上关于(λ0,μ0)为l-严格K-拟凸.

首先考虑问题Pl-SOP的LF连续性.

引理1若假设条件(H1),(H3)成立, 则LF(·,·,·)在M(μ0)×{λ0}×{μ0}上是上半连续的.

证明： 假设LF(·,·,·)在M(μ0)×{λ0}×{μ0}上不是上半连续的, 即存在y0∈M(μ0), 使得LF(·,·,·)在(y0,λ0,μ0)处不是上半连续的. 则存在LF(y0,λ0,μ0)的邻域W0, 对y0的任何邻域Vy0、λ0的任何邻域Vλ0及μ0的任何邻域Vμ0, 均存在(y,λ,μ)∈Vy0×Vλ0×Vμ0∩DLF, 使得

LF(y,λ,μ)⊄W0.

(1)

根据式(1)知, 存在序列{(yn,λn,μn)}⊂DLF, 满足(yn,λn,μn)→(y0,λ0,μ0), 使得LF(yn,λn,μn)⊄W0. 于是存在xn∈LF(yn,λn,μn), 使得

xn∉W0, ∀n∈.

(2)

由xn∈LF(yn,λn,μn)知,

F(xn,λn,μn)⊂F(yn,λn,μn)+K.

(3)

且xn∈M(μn). 又由M(·)在μ0处具有紧值且上半连续知, 存在x0∈M(μ0)及子列{xnk}⊂{xn}, 使得xnk→x0. 再由F(·,·,·)在(x0,λ0,μ0)处具有紧值且上半连续知, 存在子列{λnk}⊂{λn}, {μnk}⊂{μn}, 使得λnk→λ0,μnk→μ0. 从而必有x0∈LF(y0,λ0,μ0), 于是

F(x0,λ0,μ0)⊂F(y0,λ0,μ0)+K.

(4)

事实上, 对任何z0∈F(x0,λ0,μ0), 由F(·,·,·)在(x0,λ0,μ0)处下半连续知, 存在znk∈F(xnk,λnk,μnk), 使得znk→z0. 由式(3)知,znk∈F(ynk,λnk,μnk)+K, 存在hnk∈F(ynk,λnk,μnk), 使得

znk-hnk∈K.

(5)

由F(·,·,·)在(y0,λ0,μ0)处具有紧值且上半连续知,h0∈F(y0,λ0,μ0), 从而存在子列{hnkl}⊂{hnk}, 满足hnkl→h0. 根据式(5)及K的闭性, 有z0∈h0+K, 再由z0的任意性知式(4)成立. 因此x0∈LF(y0,μ0,λ0). 由xnk→x0知, 存在k0∈, 使得对任何nk≥k≥k0, 有xnk∈W0, 与式(2)矛盾. 所以LF(·,·,·)在M(μ0)×{λ0}×{μ0}上是上半连续的.

例1设X=Z=,Y=3,Λ×Ω=[0,1]×[0,1], 对每个(λ,μ)∈Λ×Ω,M(μ)=[0,1], 且设(λ0,μ0)=(0,0), 且

易验证上述假设满足引理1, 且对每个y∈[0,1], 有LF(y,λ0,μ0)=[0,1], 对每个(λ,μ,y)∈(0,1]×(0,1]×[0,1], 有LF(y,λ0,μ0)=[0,y]. 因此LF(·,·,·)在M(μ0)×{λ0}×{μ0}上是上半连续的.

引理2若假设条件(H2)～(H4)成立, 则LF(·,·,·)在M(μ0)×{λ0}×{μ0}上是下半连续的.

证明： 假设LF(·,·,·)在M(μ0)×{λ0}×{μ0}上不是下半连续的, 即存在y0∈M(μ0), 使得LF(·,·,·)在(y0,λ0,μ0)处不是下半连续的. 由y0∈LF(y0,λ0,μ0)知,LF(y0,λ0,μ0)≠Ø. 不失一般性, 存在x1∈LF(y0,λ0,μ0)及0X的邻域W0, {(yn,λn,μn)}⊂DLF, 满足(yn,λn,μn)→(y0,λ0,μ0), 使得

(x1+W0)∩LF(yn,λn,μn)=Ø.

(6)

下面分两种情形讨论.

情形1) 若LF(y0,λ0,μ0)为单元素集, 设xn∈LF(yn,λn,μn), 则式(3)成立, 且xn∈M(μn). 由M(·)在μ0处具紧值且上半连续知, 存在x0∈M(μ0)及子列{xnk}⊂{xn}, 使得xnk→x0. 再由F(·,·,·)在(x0,λ0,μ0)处具有紧值且上半连续知, 存在子列{λnk}⊂{λn}, {μnk}⊂{μn}, 使得λnk→λ0,μnk→μ0. 结合式(3), 类似引理1的证明知,x0∈LF(y0,λ0,μ0). 由于LF(y0,λ0,μ0)为单元素集, 因此x0=x1. 由xnk→x0知, 存在k0∈, 使得对任何nk≥k≥k0, 有xnk∈x0+W0. 于是xnk∈(x0+W0)∩LF(ynk,λnk,μnk), ∀k≥k0, 与式(6)矛盾.

情形2) 若LF(y0,λ0,μ0)不是单元素集. 不失一般性, 假设x1,x2∈LF(y0,λ0,μ0)且x1≠x2, 则F(x1,λ0,μ0)⊂F(y0,λ0,μ0)+K且F(x2,λ0,μ0)⊂F(y0,λ0,μ0)+K. 由于F(·,λ0,μ0)在M(μ0)上关于(λ0,μ0)为l-严格K-拟凸且M(μ0)为凸集, 因此对任何t∈(0,1), 均有

F(tx2+(1-t)x1,λ0,μ0)⊂F(y0,λ0,μ0)+intK.

(7)

从而对每个t∈(0,1), 均有x(t)∶=tx2+(1-t)x1∈LF(y0,λ0,μ0). 对W0, 存在0X的邻域W1, 满足W1+W1⊂W0. 显然, 存在t0∈(0,1), 使得x(t0)∈x1+W1, 因此

x(t0)+W1⊂x1+W1+W1⊂x1+W0.

(8)

由x(t0)∈M(μ0)及M(·)在μ0处下半连续知, 存在xn∈M(μn), 使得xn→x(t0). 则必存在n1∈, 使得

F(xn,λn,μn)⊂F(yn,λn,μn)+intK, ∀n≥n1.

(9)

事实上, 对任何zn∈F(xn,λn,μn), 由F(·,·,·)在(x(t0),λ0,μ0)处具紧值且上半连续知, 存在z0∈F(x(t0),λ0,μ0)及子列{znk}⊂{zn}, 使得znk→z0. 不失一般性, 不妨设zn→z0, 则由式(7)知, 存在h0∈F(y0,λ0,μ0), 使得z0-h0∈intK. 由F(·,·,·)在(y0,λ0,μ0)处下半连续知, 存在hn∈F(yn,λn,μn), 使得hn→h0. 根据极限的保号性知, 存在n1∈, 使得zn-hn∈intK, ∀n≥n1. 因此zn∈F(yn,λn,μn)+intK, 再由zn的任意性知, 式(9)成立. 由xn→x(t0)知, 对0X的邻域W1, 存在n2∈, 使得当n≥n2时, 有xn∈x(t0)+W1. 取n0=max{n1,n2}, 则当n≥n0时, 结合式(8)得

xn∈(x(t0)+W1)∩LF(yn,λn,μn)⊂(x1+W0)∩LF(yn,λn,μn),

与式(6)矛盾.

例2设X=Z=,Y=3,Λ×Ω=[0,1]×[0,1], 对每个(λ,μ)∈Λ×Ω,M(μ)=[0,1], 且设(λ0,μ0)=(0,0), 且

易验证上述假设满足引理2, 且对每个y∈[0,1], 均有LF(y,λ0,μ0)=[0,y], 对每个(y,λ,μ)∈[0,1]×(0,1]×(0,1], 均有LF(y,λ0,μ0)=[0,y]. 因此LF(·,·,·)在M(μ0)×{λ0}×{μ0}上是下半连续的.

定理1若假设条件(H2)～(H4)成立, 则S(·,·)在(λ0,μ0)处上半连续, 且S(λ0,μ0)为闭紧集.

证明： 假设S(·,·)在(λ0,μ0)处不是上半连续的, 则存在S(λ0,μ0)的邻域W0, 对λ0的任何邻域U及μ0的任何邻域N, 均存在(λ′,μ′)∈U×N, 使得S(λ′,μ′)⊄W0. 因此, 存在序列{(λn,μn)}⊂U×N, 满足(λn,μn)→(λ0,μ0), 使得S(λn,μn)⊄W0. 于是存在xn∈S(λn,μn), 使得

xn∉W0, ∀n∈.

(10)

由xn∈S(λn,μn)知,xn∈M(μn), 由M(·)在μ0处具有紧值且上半连续可知, 存在x0∈M(μ0)及子列{xnk}⊂{xn}, 使得xnk→x0. 不失一般性, 不妨设xn→x0. 则必有x0∈S(λ0,μ0). 事实上, 假设x0∉S(λ0,μ0), 则存在x′∈M(μ0), 使得F(x0,λ0,μ0)⊂F(x′,λ0,μ0)+K, 且F(x0,λ0,μ0)∉[F(x′,λ0,μ0)]l. 因此x′∈LF(x0,λ0,μ0). 对F(x0,λ0,μ0)∉[F(x′,λ0,μ0)]l, 存在0X的邻域V, 使得W′≠W0, 其中:W′=F(x′,λ0,μ0)+K+V;W0=F(x0,λ0,μ0)+K+V. 显然,W′,W0分别为F(x′,λ0,μ0),F(x0,λ0,μ0)的邻域. 对W′, 由F(·,·,·)在(x′,λ0,μ0)处具有紧值且上半连续知, 存在x′的邻域V′、λ0的邻域U0及μ0的邻域N0, 使得

F(x,λ,μ)⊂W′, ∀(x,λ,μ)∈V′×U0×N0.

(11)

对W0, 由F(·,·,·)在(x0,λ0,μ0)处具有紧值且上半连续知, 存在x0的邻域V0、λ0的邻域U00及μ0的邻域N00, 使得

F(x,λ,μ)⊂W0, ∀(x,λ,μ)∈V0×U00×N00.

(12)

再根据引理2知,LF(·,·,·)在(x0,λ0,μ0)处下半连续, 因此对x′∈LF(x0,λ0,μ0)及x′的邻域V′, 存在x0的邻域V00、λ0的邻域U000及μ0的邻域N000, 使得

V′∩LF(x,λ,μ)≠Ø, ∀(x,λ,μ)∈V00×U000×N000.

(13)

定义W″=W′W0,W00=W0W′, 则W″∩W00=Ø. 对W″, 由F(·,·,·)在(x′,λ0,μ0)处下半连续且W″∩F(x′,λ0,μ0)≠Ø知, 存在x′的邻域V″、λ0的邻域U0000及μ0的邻域N0000, 使得

F(x,λ,μ)∩W″≠Ø, ∀(x,λ,μ)∈V″×U0000×N0000.

(14)

对W00, 由F(·,·,·)在(x0,λ0,μ0)处下半连续且W00∩F(x0,λ0,μ0)≠Ø知, 存在x0的邻域V000、λ0的邻域U00000及μ0的邻域N00000, 使得

F(x,λ,μ)∩W00≠Ø, ∀(x,λ,μ)∈V000×U00000×N00000.

(15)

记Vx′=V′∩V″,Vx0=V0∩V00∩V000,Uλ0=U0∩U00∩U000∩U0000∩U00000,Nμ0=N0∩N00∩N000∩N0000∩N00000. 显然Vx′,Vx0,Uλ0,Nμ0分别为x′,x0,λ0,μ0的邻域. 由xn→x0, (λn,μn)→(λ0,μ0)知, 存在n0∈, 使得xn∈Vx0, (λn,μn)∈Uλ0×Nμ0, ∀n≥n0. 根据式(12),(13),(15), 有

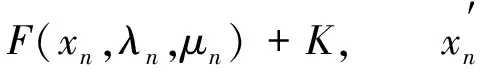
(17)

,λn,μn)+K⊂W′,

(18)

,λn,μn)+K≠F(xn,λn,μn)+K.

(19)

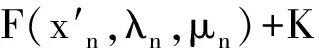
下证S(λ0,μ0)为闭集. 任取xn∈S(λn,μn),xn→x0. 由xn∈M(μn)及假设条件(H2)知,x0∈M(μ0). 类似上述证明过程可得x0∈S(λ0,μ0), 所以S(λ0,μ0)为闭集.

注3定理1的证明不同于文献[21]中定理2. 文献[21]中定理2需要F具有逆l-真性, 而在定理1中, 并不需要F具有该性质.

例3设X=Z=,Y=3,Λ×Ω=[0,1]×[0,1], 对每个(λ,μ)∈Λ×Ω,M(μ)=[0,1], 且设(λ0,μ0)=(0,0), 且

易验证上述假设满足定理1, 且对每个(λ,μ)∈[0,1]×[0,1], 均有S(λ,μ)={0,1/2}, 因此S(·,·)在(λ0,μ0)处上半连续. 但F(·,·,·)在(1,0,0)点关于(λ0,μ0)不具有逆l-真性. 事实上,F(1,0,0)⊂F(0,0,0)+K, 存在(xn,yn,λn,μn)∈(0,1/2)×(1/2,1)×(0,1]×(0,1], 满足(xn,yn,λn,μn)→(0,1,0,0), 使得F(yn,λn,μn)⊄F(xn,λn,μn)+K. 因此不满足文献[21]中定理2的条件.

假设：

(H5)F(·,λ0,μ0)在M(μ0)上关于(λ0,μ0)具有K-性, 即假设对任何x0,y0∈M(μ0), {xn},{yn}⊂M(μ0), 均有xn→x0,yn→y0, 对(λn,μn)∈Λ×Ω, 有(λn,μn)→(λ0,μ0), 且式(4)成立, 则存在n0∈, 使得当n≥n0时, 式(3)成立.

定理2若假设条件(H2)～(H5)成立, 则S(·,·)在(λ0,μ0)处下半连续.

证明： 假设S(·,·)在(λ0,μ0)处不是下半连续的, 则存在x0∈S(λ0,μ0)及x0的邻域W0, 使得对λ0的任何邻域U及μ0的任何邻域N, 均存在(λ′,μ′)∈U×N, 使得S(λ′,μ′)∩W0=Ø. 因此, 存在序列{(λn,μn)}⊂U×N, 满足(λn,μn)→(λ0,μ0), 使得

W∩S(λn,μn)=Ø.

(20)

由x0∈S(λ0,μ0)⊂M(μ0)及M(·)在μ0处下半连续知, 存在xn∈M(μn), 使得xn→x0. 根据引理2知,LF(·,·,·)在(x0,λ0,μ0)处下半连续. 因此对x0∈LF(x0,λ0,μ0)及x0的邻域W0, 存在x0的邻域V0、λ0的邻域U0及μ0的邻域N0, 使得

W0∩LF(x,λ,μ)≠Ø, ∀(x,λ,μ)∈(V0×U0×N0)∩DLF.

(21)

由xn→x0, (λn,μn)→(λ0,μ0)知, 存在n0∈, 使得当n≥n0时, 有xn∈V0, (λn,μn)∈U0×N0. 显然xn∈LF(xn,λn,μn)≠Ø, 由式(21)知,W0∩LF(xn,λn,μn)≠Ø. 设∈W0∩LF(xn,λn,μn), 则,λn,μn)⊂F(xn,λn,μn)+K， 故∈S(λn,μn).

事实上, 对任何yn∈M(μn), 有

,λn,μn)⊂F(yn,λn,μn)+K.

(22)

F(x′,λ0,μ0)⊂F(y0,λ0,μ0)+K.

(23)

则必有x′∈S(λ0,μ0). 事实上, 对任何y∈M(μ0), 满足

F(y,λ0,μ0)≤lF(x′,λ0,μ0).

(24)

再由x′∈LF(x0,λ0,μ0)知,F(y,λ0,μ0)≤lF(x0,λ0,μ0). 注意到x0∈S(λ0,μ0), 则

F(x0,λ0,μ0)≤lF(y,λ0,μ0).

(25)

注4定理2的证明不同于文献[21]中的定理4, 一般地, 定理2中假设条件(H5)成立不可少.

例4设X=Z=,Y=3,Λ×Ω=[0,1]×[0,1], 对每个(λ,μ)∈Λ×Ω,M(μ)=[0,1], 且设(λ0,μ0)=(0,0), 且F(x,λ,μ)=(λ·[0,2-x],μ·[0,2-x],[0,1]). 易验证满足假设条件(H2)～(H4), 且

因此S(·,·)在(λ0,μ0)处不是下半连续的. 但假设条件(H5)不满足. 事实上, 存在(x0,y0)=(1,0), 有F(x0,λ0,μ0)⊂F(x0,λ0,μ0)+K对任何的序列(xn,yn,λn,μn)∈(3/4,1)×(0,1/2)×(0,1]×(0,1], 满足(xn,yn,λn,μn)→(x0,y0,λ0,μ0), 使得F(xn,λn,μn)⊄F(yn,λn,μn)+K, ∀n∈.

由定理1与定理2知,S(·,·)在(λ0,μ0)处连续, 可得如下推论：

推论1若假设条件(H2)～(H5)成立, 则S(·,·)在(λ0,μ0)处连续.

综上, 本文在拓扑向量空间中, 通过引进一类广义集值优化问题l-SOP与含参广义集值优化问题Pl-SOP, 给出了问题l-SOP的l-最小解与问题Pl-SOP的l-最小解的概念, 并讨论了问题Pl-SOP的LF连续性, 在此基础上, 结合集值映射的l-严格K-拟凸性, 得到了问题Pl-SOP的l-最小解的连续性定理.