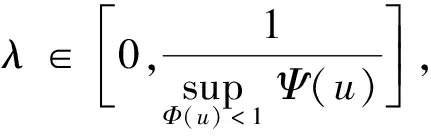张 申 贵

(西北民族大学 数学与计算机科学学院, 兰州 730030)

0 引 言

考虑如下分数阶椭圆型方程:

(1)

其中:Ω是N中具有局部Lipschitz边界∂Ω的有界开集,N>ps,s∈(0,1),p∈(1,+∞); 参数λ≥0;F(x,u)=f(x,s)ds. 设A(t): [0,+∞)→+和B(t):→为连续函数.

分数阶微分方程在控制论、电化学和神经元等领域应用广泛. 目前, 关于分数阶椭圆型方程的研究已有很多结果, 如: 文献[3]讨论了分数阶Sobolev空间的性质; 文献[4]研究了一类带有临界指数的分数阶Kirchhoff型方程的可解性; 当非线性项带有参数时, 文献[5]讨论了分数阶Laplace方程非平凡解的存在性和分歧问题; 文献[6]研究了分数阶Laplace方程在自由边界上的变分问题; 当p=2,A(t)=B(t)=1时, 文献[7-8]利用山路定理研究了问题(1)多重解的存在性; 文献[9]利用Morse理论和计算临界群的方法, 得到了分数阶p-Laplace方程

非平凡解的存在性, 其中方程右端的非线性项f(x,u)满足(AR)型超线性条件: 即存在μ>p,L>0, 使得

0<μF(x,u)≤f(x,u)u

其中函数K:N{0}→(0,+∞)满足:

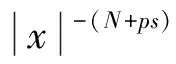
∀t∈.

本文在一类不同于(AR)条件的超线性条件下, 利用文献[13]中建立的临界点定理研究问题(1)非平凡解存在的充分条件.

1 预备知识

定义1[9]分数次Sobolev空间Ws,p(N)定义为

其中S表示可测实值函数组成的集合. 记

X(Ω)={u∈Ws,p(N)|u(x)=0, a.e.x∈NΩ},

X(Ω)上的范数为

引理2[9]记

∀u,v∈X(Ω).

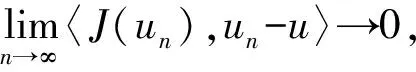
引理3(临界点定理)[13]设X为Banach空间, 泛函Iλ∈C1(X,), 且下列条件成立:

2) 泛函Iλ下方无界;

3) 记泛函Iλ∶=Φ-λΨ, 且Φ,Ψ∈C1(X,)满足Φ下方有界,Φ(0)=Ψ(0)=0. 给定r>0, 对每个有则对于泛函Iλ至少有两个非平凡的临界点.

若对∀v∈X(Ω), 有

则称u∈X(Ω)为问题(1)的弱解.

在X(Ω)上定义能量泛函Iλ如下:

其中:

则Iλ(u)∈C1(X(Ω),), 且

从而u∈X(Ω)是问题(1)的(弱)解等价于u是泛函Iλ的临界点.

2 主要结果

假设下列条件成立:

(H1) 设存在常数a0>0, 使得对所有的t∈[0,+∞)，A(t)≥a0均成立；

(H2) 设存在常数η≥1, 使得对所有的t∈[0,+∞)，

均成立；

(H3) 设存在常数b0>0,b1>0, 使得对所有的t∈,b0≤B(t)≤b1均成立;

(H6) 设存在常数L>0,c1>0,c2>0, 使得:

1) 当|u|≥L时, 有

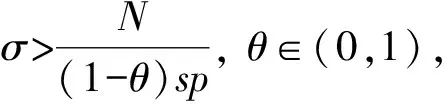
本文主要结果如下:

定理1设条件(H1)～(H7)成立, 则存在λ*>0, 使得对每个λ∈[0,λ*], 问题(1)均至少有两个非平凡解.

证明: 1) 证明泛函Iλ满足(C)条件. 设{un}⊂X(Ω)为泛函Iλ的(C)序列, 则

(un)‖≤c3, |Iλ(un)|≤c3.

(2)

首先, 证明序列{un}在X(Ω)中有界. 假设{un}在X(Ω)中无界, 则当n→∞时,

‖un‖→+∞.

(3)

且

(4)

由假设条件(H2)～(H4)和式(3), 有

由假设条件(H5)及(H6)中1)知, 存在常数c5>0, 使得对所有的x∈Ω和u∈,

(7)

均成立. 结合式(6),(7), 有

(8)

(9)

结合式(5),(9), 当n→∞时, 有

(10)

当n充分大时, 由条件(H6)中2)及式(6), 有

(11)

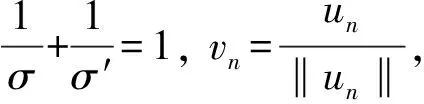
由假设条件(H1),(H3), 有

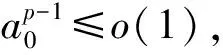
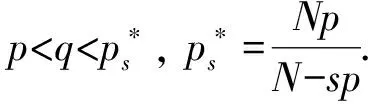
记

∀u,v∈X(Ω).

2) 证明泛函Iλ满足引理3中条件2). 令

由假设条件(H2), 有

(14)

利用假设条件(H4)同理可证, 存在c9>0,c10>0, 使得对∀t∈时, 有

(15)

由假设条件(H7), 对于∀υ>0, 存在c11>0, 使得

(16)

对所有的x∈Ω和u∈成立. 取u0∈X(Ω){0}, 对于t>1, 由式(14)～(16)及λ≥0, 有

令υ充分大, 使得

3) 证明泛函Iλ满足引理3中条件3). 记

Iλ(u)∶=Φ-λΨ∈C1(X(Ω),),

其中:

由条件(H1), 有

(18)

式(18)表明, 泛函Φ下方有界, 且对于u∈X(Ω), 满足Φ(u)<1, 有

‖u‖

(19)

(20)

(21)

结合假设条件(H3),(H5)及式(19)～(20), 对于u∈X(Ω), 且满足Φ(u)<1, 有

注1令非局部系数A(t)=a+bpt, 其中:t≥0;p∈(1,+∞);a和b为正常数. 则函数A(t)满足条件(H1)和(H2).

事实上,A(t)=a+bpt≥a>0, 易见a0=a. 取η=p, 对t≥0, 有

令B(t)=arctant+π, 则有

从而B(t)满足条件(H3),(H4). 取A(t)=B(t)=1, 此时η=1, 令p=2, 且

则F满足定理1中条件, 但不满足(AR)条件, 也不满足文献[2-12]中定理的条件.