张家娇，吴宜均

（天津师范大学数学科学学院，天津300387）

1 引言和预备知识

图的染色理论源于四色问题，图的染色理论在离散数学中具有重要的地位，其在交通规划、网络通信和经济分析等方面有广泛的应用.

设G为一个简单图，分别用E（G）和V（G）表示图G的边集合和顶点集合.对于任意顶点v∈V（G），用NG（v）表示图G中与顶点v相邻的顶点集合，定义|NG（v）|为顶点的度，记为 d（v）.Δ（G）=max{d（v），v∈G}定义为图G的最大度.图G的正常点染色是一个映射 c：V（G）→{1，2，…，k}，满足任意 2 个相邻的顶点 u、v∈V（G）染不同的颜色，即 c（u）≠c（v）.文献[1]提出了图的动态染色的概念，图G的动态染色是一个正常点染色 c，满足对任意顶点 v∈V（G），若 d（v）≥2，则c（|NG（v）|）≥2，使图G存在动态染色的最小色数k称为图G的动态色数，记为χ2（G）.之后许多学者对动态染色进行了研究.文献[2]证明了除C5外，对于所有的平面图都有χ2（G）≤4；文献[3]研究了动态色数的上界；文献[4]定义了图的列表动态染色，并研究了图的动态染色与列表动态染色的关系；文献[5]给出了一些特殊图的动态色数的上界；文献[6]研究了χ2（G）与χ2（G-e）的差，及χ2（G）与χ2（G-v）的差，其中e∈E（G），v∈V（G）；文献[7]研究了图的色数与动态色数差的上确界.

图G的一个r-多彩染色是一个正常的顶点染色，使得对于任意顶点v∈V（G），并且d（v）≥2，有c（|NG（v）|）≥min{d（v），r}，使得图G有r-多彩染色的最小的整数k称为图G的r-多彩色数，用χr（G）表示.显然2-多彩染色即为动态染色.文献[8]证明了若平面图G的围长不小于6，则有χr（G）≤r+5；文献[9]研究了没有K4-图子式的图的r-多彩染色；文献[10]研究了列表3-动态染色与图的最大平均度的关系.

对于给定的图G和H，直积图G×H=（V，E），其中：

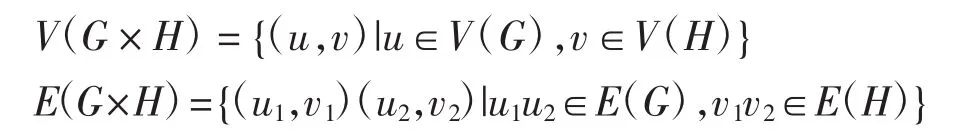
显然有 Δ（G×H）= Δ（G）Δ（H）.本文研究圈和圈的直积图的多彩染色.

文献[1]定义了图 Gm，n=（Vm，n，Em，n），其中点集和边集分别为

在此定义的基础上，当n是奇数时，直积图Pm×Cn与Gm，2n同构，同构的对应关系为

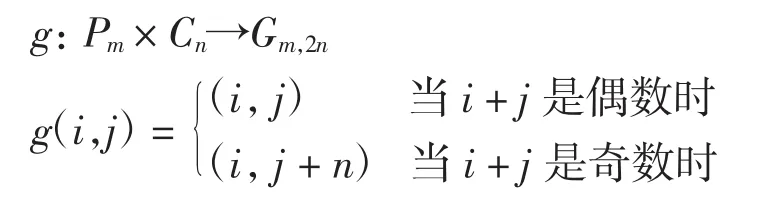
当n是偶数时，直积图Pm×Cn与2Gm，n同构.

在直积图Pm×Cn中加入边集合F={（m，j）（1，j′）|j′≡j± 1（mod n）}，即可得到直积图 Cm× Cn，进而将边集合 g（F）加到 Gm，2n中，则可得到 Cm× Cn的同构图.

定义图，其中：

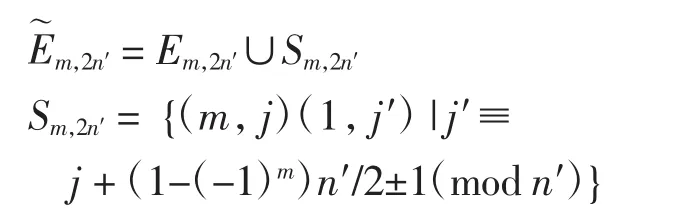
并且当 n为奇数时，令Sm，2n=g（F）；当 n为偶数时，令2Sm，2n=g（F）.则有

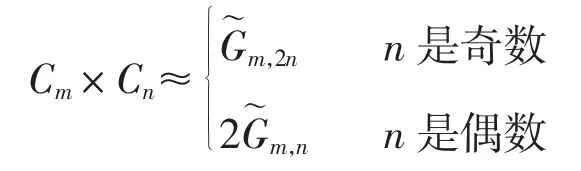
所以，当n是奇数时，；当n是偶数时，.图1（a）为直积图C4×C7，图1（b）为与 C4× C7同构的图.

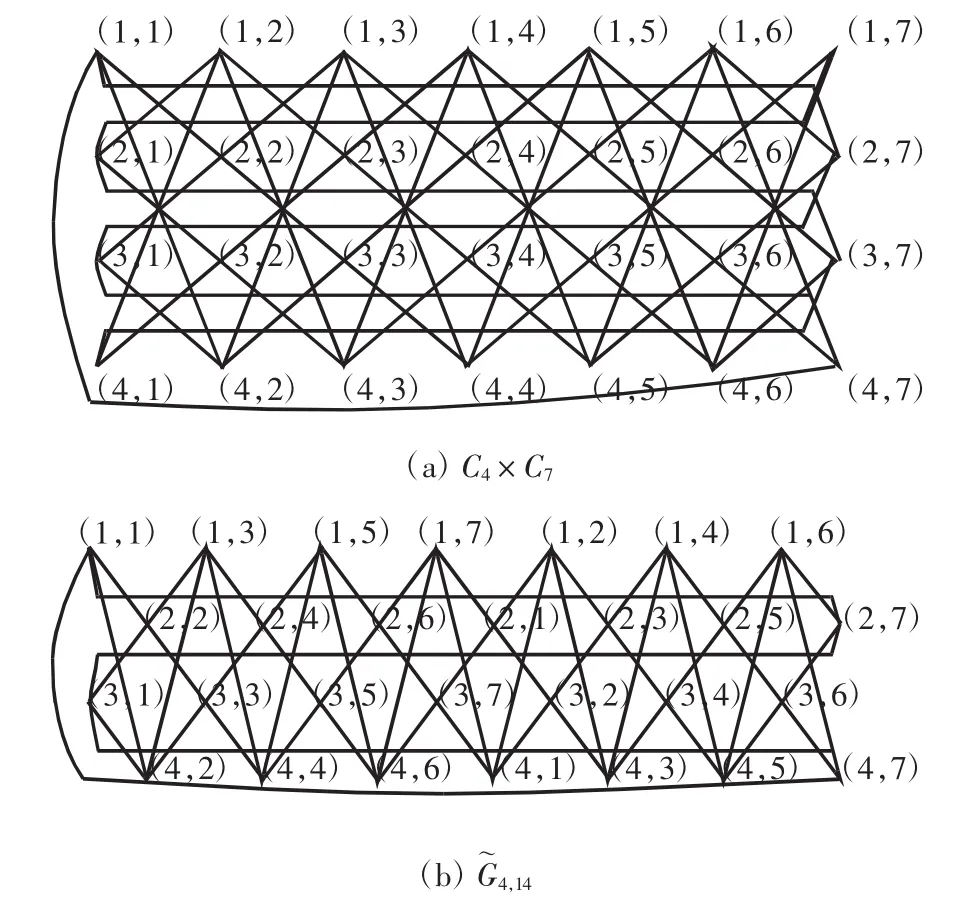
图1 直积图C4×C7和与其同构的图4，14Fig.1 Direct product C4 × C7and its isomorphic graph 4，14

2 Cm×Cn的多彩染色

定理1设m、n为不小于3的正整数，则有

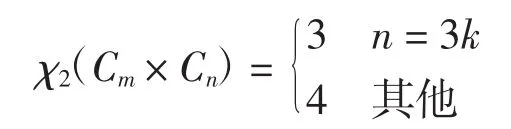
证明 情况1n是偶数.

当n=6k时，根据多彩染色的定义，|c（NG（v））|≥min{d（v），r}，因此|c（V（G））|≥χr（G）≥min{Δ（G），r}+1，所以有χ2（Cm×Cn）≥3.

Cm和 Cn是 2 个简单图，Cn的最小度 δ（Cn）=2，设Cn的r-多彩染色为c1，对于直积图Cm×Cn，可定义Cm×Cn的r-多彩染色c（（u，v））=c1（u），u∈Cm，v∈Cn，易证，因此.因为χ2（C6k）=3，所以有χ2（Cm×C6k）≤χ2（C6k）=3.综上，当n=6k时，有χ2（Cm×Cn）=3.

当n=6k+2或n=6k+4时，有3≤χ2（Cm×Cn）≤4.事实上，Cm×Cn中任意2个相邻的顶点都在一个4-圈中，因此可得χ2（Cm×Cn）≥4.故此时有χ2（Cm×Cn）=4.

情况2n是奇数.

当n是奇数时，根据预备知识，有Cm×Cn同构于，而的 2-多彩色数的证明方法与情况 1 一致.

定理2设m为不小于3的正整数，则有

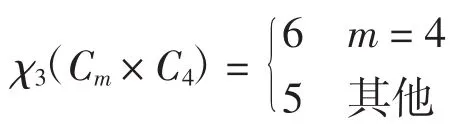
证明因为Δ（Cm×C4）=4，根据|c（V（G））|≥χr（G）≥r+1，有 χ3（Cm× C4）≥4.

使用反证法.假设χ3（Cm×C4）=4.由预备知识知Cm×C4同构于，因此需求出的具体数值.

（1）如果 c（u1，v1）=1，c（u2，v4）=2，c（u2，v2）=3，c（um，v2）=4 或 c（um，v4）=4，那么 c（u1，v3）=1，c（u3，v1）≠c（u3，v3），并且 c（u3，v1）、c（u3，v3）∉{1，2，3}，因此（u2，v2）不满足 3-多彩染色的条件.

（2）如果 c（u1，v1）=1，c（u2，v4）=2，c（um，v2）=3，c（um，v4）=4，那么 c（u1，v3）=1，c（u3，v1）≠c（u3，v3），并且 c（u3，v1）、c（u3，v3）∉{1，2}，不失一般性，假设 c（u3，v1）=3，c（u3，v3）=4，那么 c（u2，v2）=2，并且 c（u4，v2）≠c（u4，v4），c（u4，v2）、c（u4，v4）∉{2，3，4}，因此（u3，v3）不满足3-多彩染色的条件.

（3）如果 c（u1，v1）=1，c（u2，v2）=2，c（um，v2）=3，c（um，v4）=4，那么 c（u1，v3）=1，不失一般性，设 c（u3，v1）=3，c（u3，v3）=4，那么 c（u2，v4）=2，c（u4，v2）≠c（u4，v4），并且 c（u4，v2）、c（u4，v4）∉{2，3，4}，因此（u3，v3）不满足3-多彩染色的条件.

综上，4种颜色不能使图满足3-多彩染色，因此有.

当m≠4，且m为偶数时，下面给出G~m，4的一个用5种颜色的3-多彩染色c.

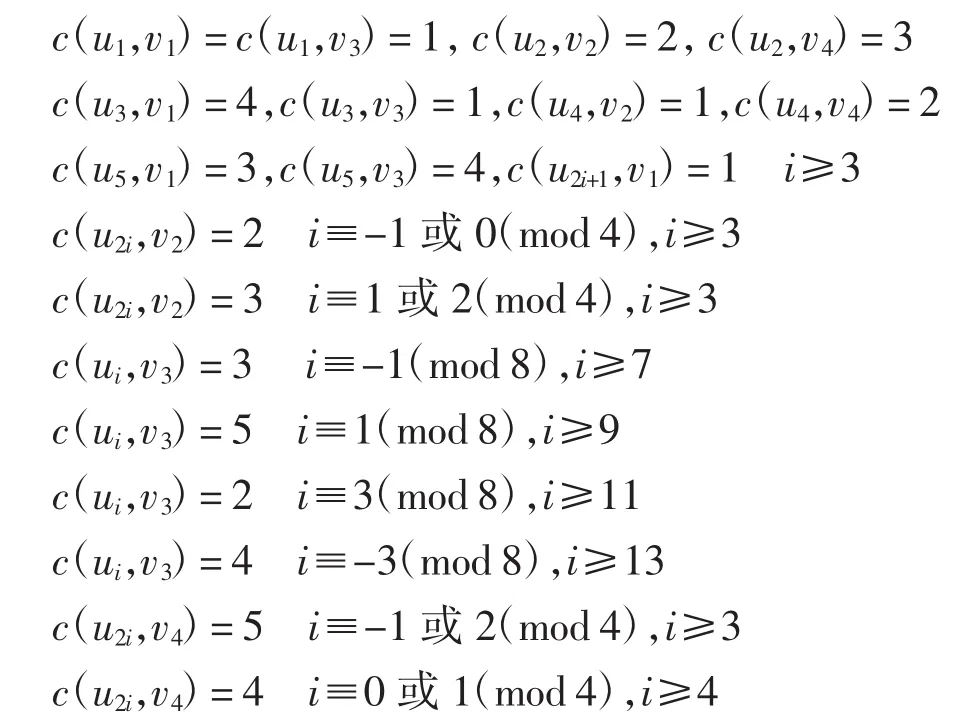
图2为的染色 c的前 18 行，根据图的特征，只需要将第6行到第13行的染色方法向后复制，如果有必要删去若干行，便得到图的5种颜色的染色.在这个染色中，有|c（N（ui，vj））|=3，满足3-多彩条件，因此有.综上有.

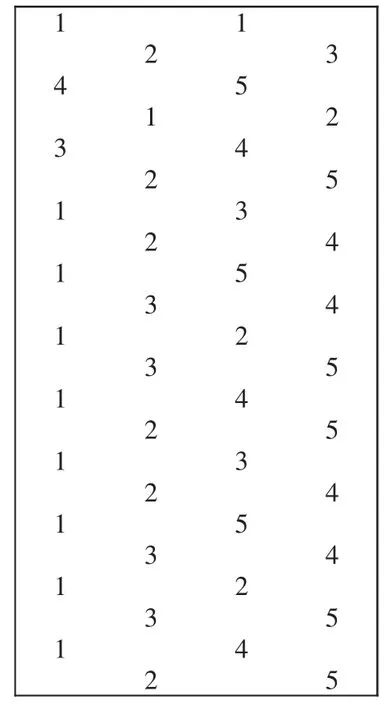
图2 图m，4的前18行的3-多彩染色Fig.2 First 18 lines of 3-hued coloring ofm，4

当m≠4，且m为奇数时，的3-多彩染色与上述染色相同.因此.

当m=4时，假设，不失一般性，如果c（u1，v1）=1，顶点（u1，v1）的邻点必须染有至少 3 种不同的颜色，而顶点（u1，v1）、（u3，v1）、（u1，v3）有相同的邻点集合，因此顶点（u3，v1）和顶点（u1，v3）的可用颜色数至多为2种，并且颜色1一定属于顶点（u3，v1）和顶点（u1，v3）的可用颜色集合.因此顶点（u2，v2）不能满足 3-多彩条件，于是有.图3给出了的一个用6种颜色的染色，在这个染色中，任意相邻2点的颜色不同，且|c（N（ui，vj））|=3，满足3-多彩条件，因此.综上有.

图3 图4，4的3-多彩染色Fig.3 3-hued coloring of4，4

[1]MONTGOMERY B.Dynamic Coloring of Graphs[D].Morgantown：West Virginia University，2001.

[2]LAI H J，MONTGOMERY B，POON H.Upper bounds of dynamic chromatic number[J].Ars Combinatoria，2008，68（1）：193-201.

[3]丁超，樊锁海，赖宏建.图的条件染色的上界[J].暨南大学学报（自然科学版），2008，29（1）：7-14.DING C，FAN S H，LAI H J.Upper bound on conditional chromatic number of graphs[J].Journal of Jinan University（Natural Science），2008，29（1）：7-14（in Chinese）.

[4]KIM S J，SANG J L，PARK W J.Dynamic coloring and list dynamic coloring of planar graphs[J].Discrete Applied Mathematics，2013，161（13/14）：2207-2212.

[5]KIM B M，SONG B C，RHO Y.2-distance colorings of some direct products of paths and cycles[J].Discrete Mathematics，2014，338（10）：1730-1739.

[6]MIAO L Y，LAI H J，GUO Y F.Element deletion changes in dynamic coloringofgraphs[J].DiscreteMathematics，2016，339（5）：1600-1604.

[7]郭燕芳.关于图的动态染色的研究[D].徐州：中国矿业大学，2016.GUO Y F.The Study of the Dynamic Coloring of Graphs[D].Xuzhou：China University of Mining and Technology，2016（in Chinese）.

[8]SONG H M，LAI H J，WU J L.On r-hued coloring of planar graphs with girth at least 6[J].Discrete Applied Mathematics，2016，164（2）：251-263.

[9]SONG H，FAN S，CHEN Y，et al.On r-hued coloring of K4-minor free graphs[J].Discrete Mathematics，2014，315（1）：47-52.

[10]KIM S J，PARK B.List 3-dynamic coloring of graphs with small maximumaveragedegree[J].DiscreteMathematics，2017，arXiv：1609.05824.