朱佳佳，陈 蕾，王同科

（天津师范大学数学科学学院，天津300387）

Mellin变换是一类重要的积分变换，在数学[1-2]、物理[3]和工程中的一些领域，如数论、概率论、计算机科学、量子力学、图像识别等方面有着广泛的应用.对于定义在（0，+∞）上的函数f（x），其Mellin变换定义为[1-2]

其中s=σ+it（σ、t∈R）为复数.

Mellin变换并不是对所有的s都成立，使得M（s）成立的s的范围称为基本条带[2].对于一些常见函数，文献[4]给出了Mellin变换表.对于更复杂的函数，需要通过数值积分方法[5-6]计算其在一些点的离散Mellin变换.当f（x）在[0，+∞）上非充分光滑时，积分（1）为奇异积分，其计算比较困难.文献[7-8]利用函数在奇点处的Puiseux级数展开式设计了计算积分的有效方法.本文假定f（x）在x=0和x=+∞存在Puiseux级数展开式，在此基础上研究Mellin变换的高精度Gauss-Legendre求积方法.

1 函数的Puiseux级数展开式及其在数值积分中的应用

对于非充分光滑或在某些点奇异的函数，其Taylor级数不存在，但是Puiseux级数[8]可能存在.Puiseux级数是幂级数的一种推广，其展开式中可以包含负指数幂、分数指数幂和对数因子，它们被广泛用于描述微分方程的解在奇点的性态.函数在某个点的Puiseux级数可以通过符号计算得到.

设f（x）是定义在区间（a，b]上的函数，在端点x=a处分数阶代数和对数奇异，x=a处的Puiseux级数展开式为

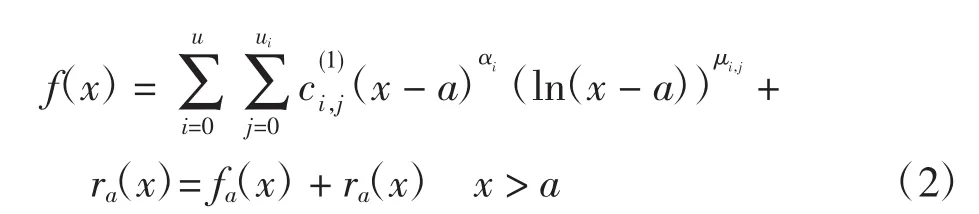
除端点x=a外，f（x）在其他点充分光滑.以步长h=（b-a）/n将[a，b]分割为n个子区间，对于积分I=其复合Gauss-Legendre求积公式为

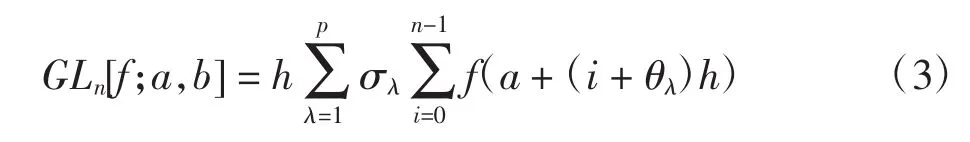
其中：p为节点个数；σλ＞0为权重；节点 θλ∈（0，1），λ=1，2，…，p.这些权重和节点可由一些高效算法[9]求出.

引理[8]设f（x）在端点x=a处代数和对数奇异，Puiseux级数展开式（2）成立，则计算积分的改进Gauss-Legendre求积公式为

误差主项为

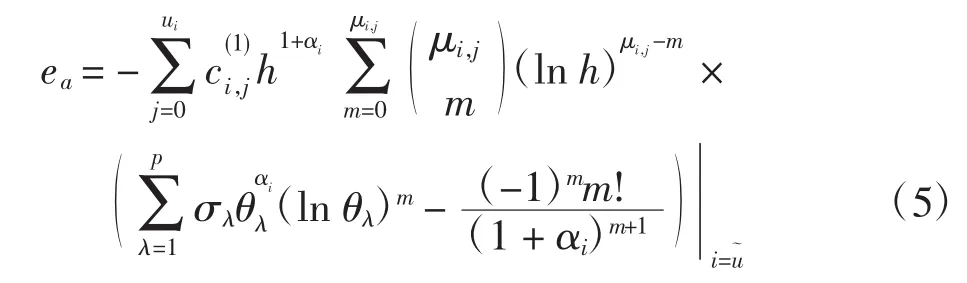
2 Mellin变换的Gauss-Legendre求积算法

2.1 Mellin变换成立的条件

假设定义在区间（0，+∞）上的函数f（x）能够在零点和无穷远点进行Puiseux级数展开，下面分别在区间（0，1）和（1，+∞）上对Mellin变换成立的条件进行讨论.

根据Mellin变换的定义（1），M（s）可化为如下形式

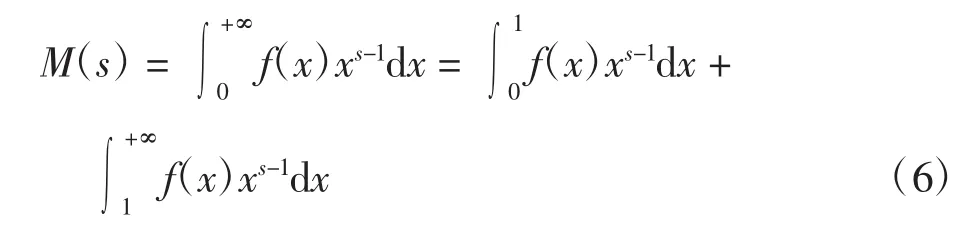
对式（6）中第2个积分做变量替换t=1/x，并记g（t）=f（1/t），则有

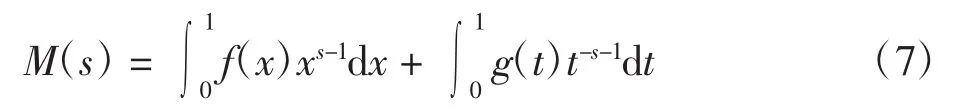
式（7）右端2个积分具有相同的形式，为方便，记

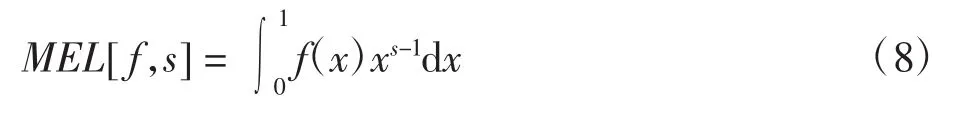
则式（7）变为

由此可知，Mellin变换成立的充分必要条件为MEL[f，s]和MEL[g，-s]均可积.接下来对这2个积分是否存在进行讨论，为方便，只考虑s为实数的情形.

定理1设f（x）=xα（ln x）μ，其中：α为实数，μ为非负整数，则积分MEL[f，s]存在的充分必要条件为s＞-α

证明对MEL[f，s]进行分部积分，得

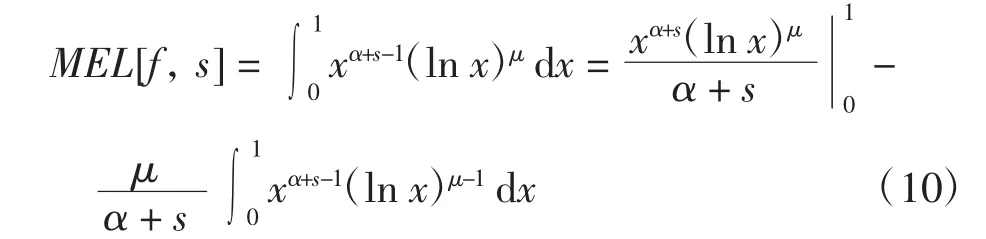
显然，当且仅当α+s＞0时，上式才有意义.所以积分MEL[f，s]存在的充分必要条件为s＞-α.

定理2设f（x）在x=0和x=+∞存在Puiseux级数展开式，即有

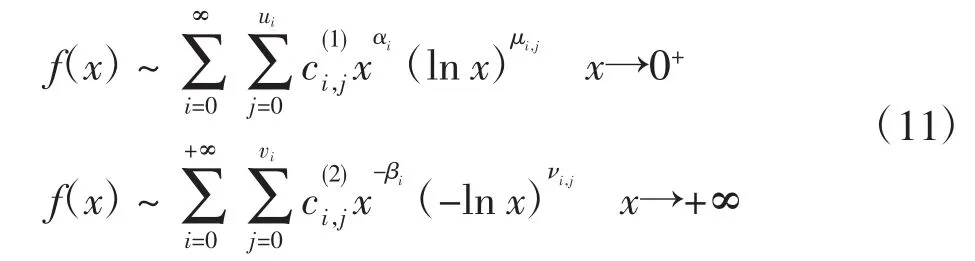
其中：αi、βi均为实数，满足 α0＜ α1＜ α2＜ …，β0＜ β1＜β2＜ …，μi，j、νi，j为非负整数，则 Mellin 变换存在的充分必要条件为-α0＜s＜β0.

注：（-α0，β0）即为 Mellin 变换存在的基本条带.

证明由渐近分析知

由定理1可知，MEL[f，s]存在的充分必要条件为s＞-αi，MEL[g，-s]存在的充分必要条件为-s＞ -βi.由 αi、βi满足的条件知，当且仅当-α0＜ s＜ β0时，MEL[f，s]和MEL[g，-s]均存在，即 Mellin 变换 M（s）存在的充分必要条件为-α0＜ s＜ β0.

2.2 Gauss-Legendre求积算法

这里仍假定f（x）在x=0和x=+∞存在Puiseux级数展开式（11）.首先，由式（11）可知

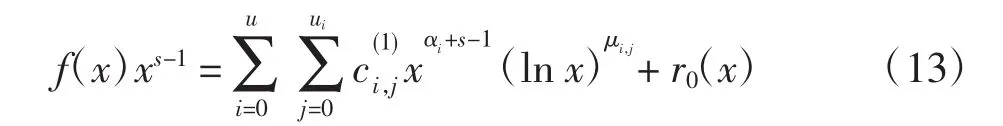
对MEL[f，s]，将区间[0，1]剖分为n等份，步长为h=1/n.由式（3）可得

其误差主项为

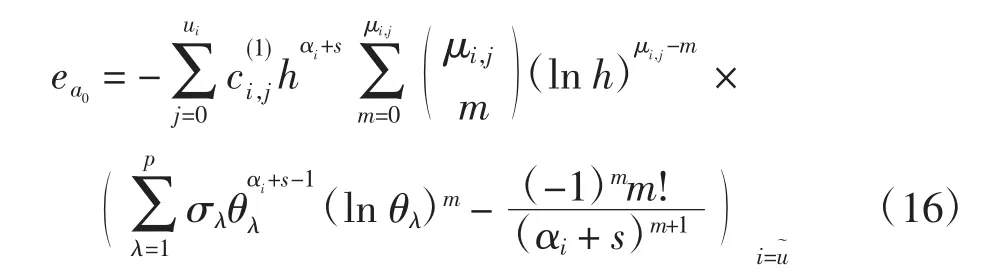
其次，由于 MEL[g，-s]与 MEL[f，s]具有相同的形式，与上述过程类似，可得到

进一步可得到

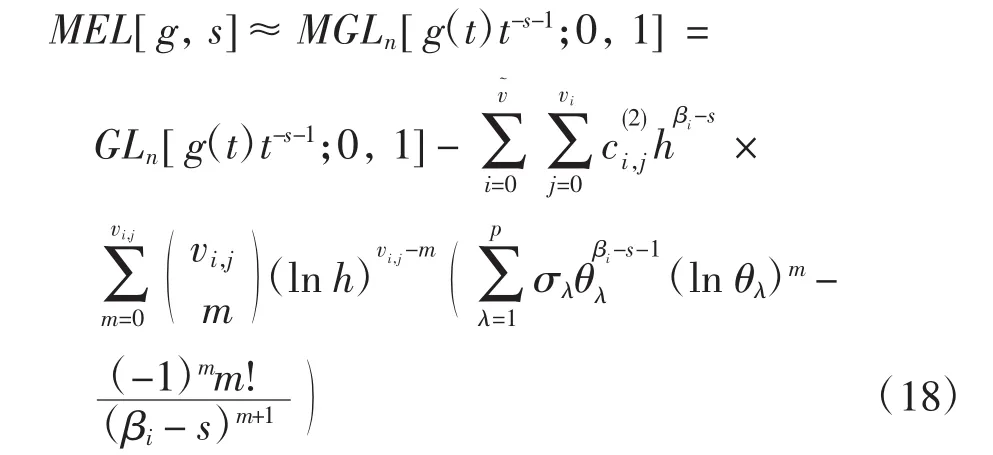
其误差主项为

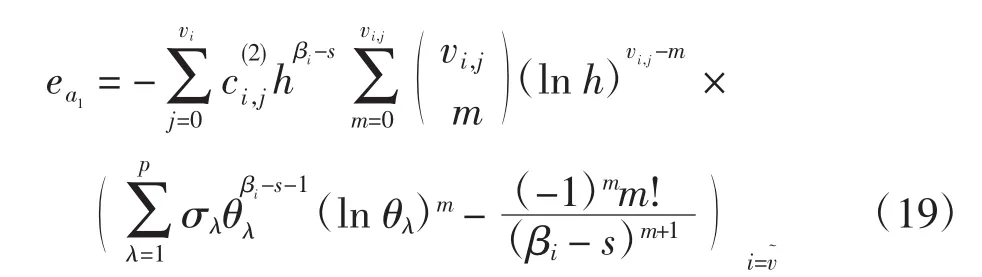
综上，由式（9）可得 Mellin变换（1）的 Gauss-Legendre计算公式为

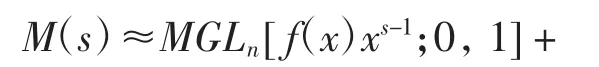
误差主项为

3 Mellin变换计算实例

本节给出一些计算实例以说明算法的有效性和高精度.对于本文给出的算法，使用Mathematica软件[10]编写程序并计算.式（14）、（15）和（18）中的计算参数分别取为

例1计算的Mellin变换的数值解.

直接对f1（x）在x=0和x=+∞处进行Puiseux展开，得

由此得 Mellin变换成立的条件是 s∈（1/3，1/2）.使用改进的Gauss-Legendre求积方法计算该Mellin变换在一些点的数值解，再利用Mathematica软件中的NIntegrate命令计算其更高精度的近似解作为其真实值，计算结果见表1.

表1 f1的Mellin变换在一些s处的计算值与误差Tab.1 Calculated values and errors of Mellin transform of f1at s

例2计算的Mellin变换的数值解（Kn（z）为第二类修正Bessel函数）.

查表[4]可知f（x）=exK0（x）的Mellin变换为M（s，f）=π-1/22-sГ（1/2+s）Г2（s），其中Г（z）为Gamma函数，于是

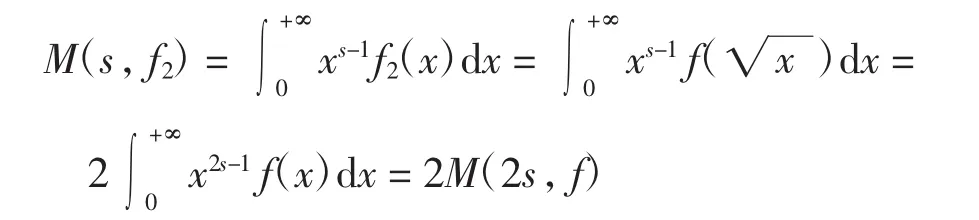
由此可得f2（x）的Mellin变换在不同s值下的真实解，进而得到实际误差.

直接计算得f2（x）在x=0和x=+∞处的Puiseux级数展开式为

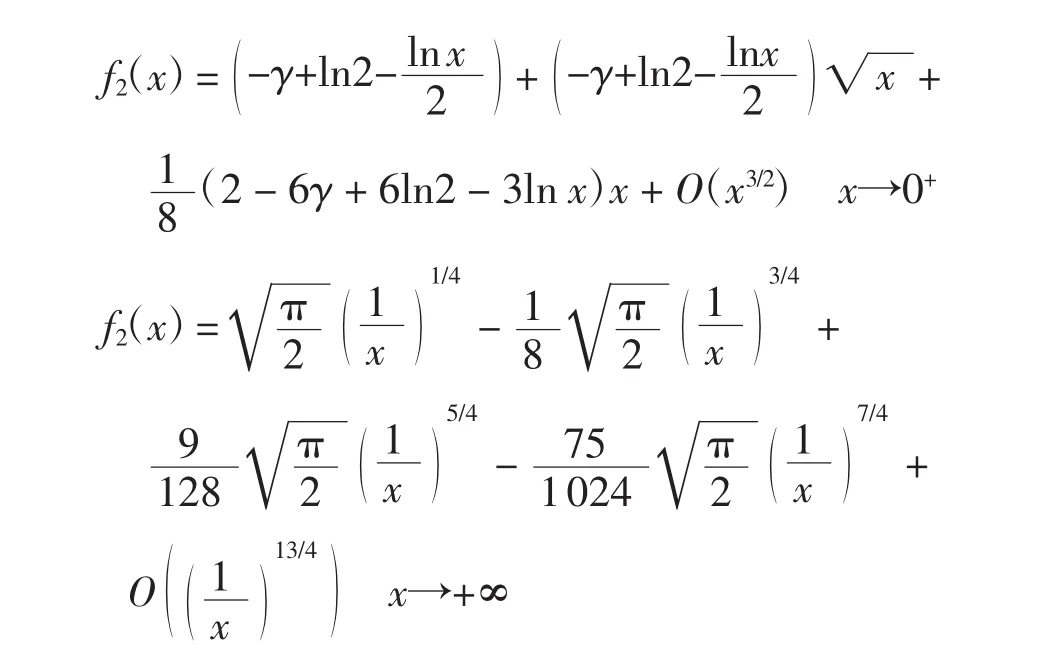
故Mellin变换成立的条件为s∈0，1/（）4.使用改进的Gauss-Legendre求积方法计算该变换，结果见表2.

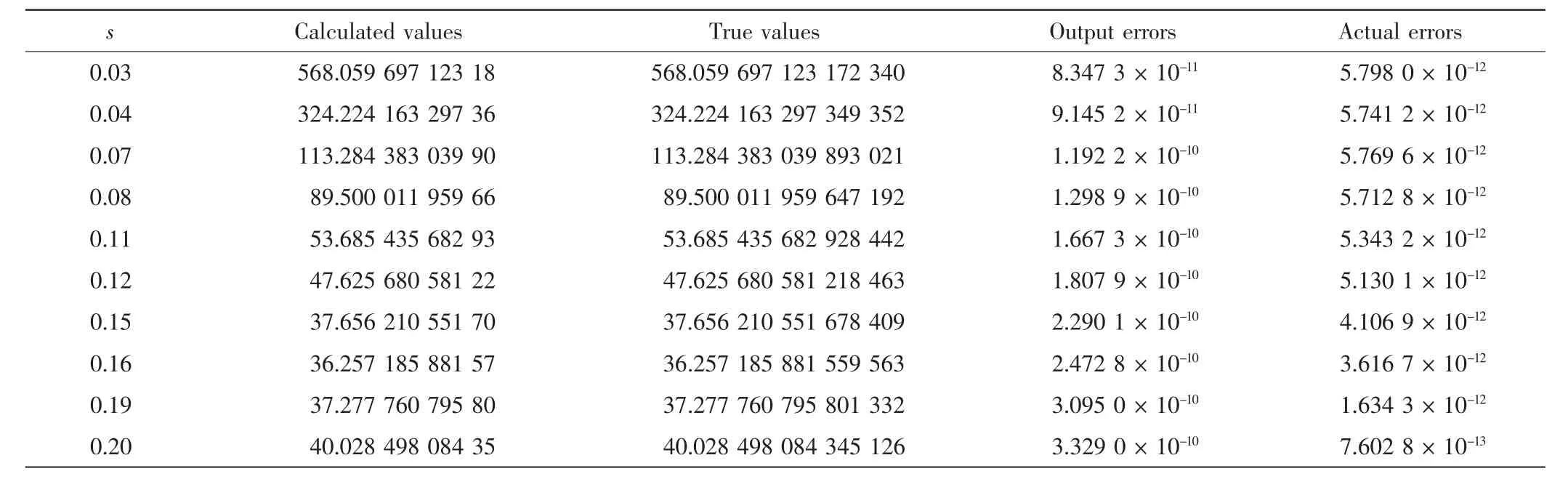
表2 f2的Mellin变换在一些s处的计算值与误差Tab.2 Calculated values and errors of Mellin transform of f2at s

以上2个算例函数在零点及无穷远点均为分数阶可导或对数奇异，本文算法的误差介于10-12和10-16之间，且输出误差与真实误差比较符合，算法的正确性和准确性得以保证.对于在零点和无穷远点代数和对数奇异的函数，本文方法为其Mellin变换的数值求解提供了一种新的途径.

参考文献：

[1] 沈克精.梅林（Mellin）变换及其应用[J].安徽大学学报：自然科学版，1992，3：15-22.SHEN K J.Mellin transform and it′s application[J].Journal of Anhui University：Natural Science Edition，1992（3）：15-22（in Chinese）.

[2]PHILIPPE F，XAVIER G，PHILIPPE D.Mellin transforms and asymptotics：Harmonic sums[J].Theoretical Computer Science，1995，144（1/2）：3-58.

[3] 郑师海，杨国桢，林清景，等.实现Mellin变换的一种新方法[J].物理学报，1986，35（4）：529-534.ZHENG S H，YANG G Z，LIN Q J，et al.A new method for performing optical Mellin transform[J].Acta Physica Sinica，1986，35（4）：529-534（in Chinese）.

[4]FRITZ O.Tables of Mellin Transforms[M].New York：Springer-Verlag，1974.

[5] DAVIS P J，RABINOWITZ P.Methods of Numerical Integration[M].2nd Edtion.Orlando：Academic Press，1984.

[6]RAFAEL G C，FRANCISCO M D.Quadrature formulas for the Laplace and Mellin transforms[J].BIT Numerical Mathematics，2009，49（3）：477-486.

[7]WANG T K，LI N，GAO G H.The asymptotic expansion and extrapolation of trapezoidal rule for integrals with fractional order singularities[J].InternationalJournalofComputerMathematics，2015，92（3）：579-590.

[8] WANG T K，LIU Z F，ZHANG Z Y.The modified composite Gauss type rules for singular integrals using Puiseux expansions[J].Mathematics of Computation，2017，86（303）：345-373.

[9] KNUT P.On the computation of the Gauss-Legendre quadrature formula with a given precision[J].Journal of Computational and Applied Mathematics，1999，112（1/2）：253-267.

[10]王同科，张东丽，王彩华.Mathematica与数值分析实验[M].北京：清华大学出版社，2011.WANG T K，ZHANG D L，WANG C H.Mathematica and Numerical Analysis Experiment[M].Beijing：Tsinghua University Press，2011（in Chinese）.