宋 明， 和兴锁， 闫业毫， 和东生

(西北工业大学 力学与土木建筑学院，陕西 西安 710029)

0 引言

太阳帆是利用巨大的、像镜子一样的轻质帆面反射太阳光来产生推动力的.由日本航天局研制的“IKAROS”太阳帆成功发射后[1]，基于太阳帆的一系列空间任务被相继提出，如：NanoSail-D, Cubesail, DeorbitSail, Sunjammer，LightSail等.毫无疑问，太阳帆将会成为本世纪的热门研究课题.

限制性三体问题模型一直被视为基本的动力学模型[2]，而希尔型三体问题是限制性三体问题的一种近似[3].通常情况下人们把天体视为质量均匀分布的理想球体，不考虑质量为无穷小量的太阳帆对天体运动的影响.但是，宇宙中纯粹意义的球体是不存在的，大部分星体都是扁的，也有一部分是不规则形状的.Sharma[4]发现考虑大天体扁率的限制性三体系统存在周期性轨道.Singh[5]把诸如天体扁率、天体的辐射等多种扰动影响结合在一起，分析平衡点的非线性稳定性.Douskos[6]对希尔型三体问题的平衡点及其稳定性进行了系统研究.遗憾的是，以上文献没有涉及到天体扁率对太阳帆轨道的影响.因此，笔者主要研究天体扁率在希尔型三体系统中对太阳帆运动的影响，以及共线平衡点附近的悬浮轨道设计.

1 太阳帆力学模型

“IKAROS”太阳帆上的反射控制设备，简称RCD，是一种柔性多层液晶薄片通过改变其上的电压来改变反射率的装置[7].龚胜平等[8]提出了一种RCD，其中包含两种模块：镜面反射模块和吸收光线模块，并把这种技术成功运用在研究地月系统平衡点太阳帆轨道运动和研究太阳帆在小行星附近的动力学[9-10].笔者将会利用这一技术并进行一些改进.改进型的RCD包含两种模块，一种是反射模块，反射系数为ρr；另外一种是吸收模块，吸收系数为ρa=1-ρr.和之前版本的RCD不同的是，笔者把散射和热辐射一并考虑在内.假设RCD可以转换成开启和关闭两种状态.太阳帆总的有效面积为Atot，设定RCD的面积为A0=Atot/8，吸收模块的面积为Aa=pAtot,p∈[0,0.125]，其中p为比例系数，吸收模块对应的状态为关闭；同样反射模块的面积为Ar=Atot-Aa，对应开启状态.于是，因吸收、反射和热辐射作用而产生的太阳帆加速度可以表示为：

αns；

(1)

(2)

(3)

式中，P表示太阳光压；太阳帆帆面法向量为n=(cosαcos (ωst),-cosαsin (ωst),sinα)T；ns=(cos (ωst),-sin (ωst),0)T表示太阳光线方向矢量；太阳帆质量为m；α是帆面法向量与光线的夹角；ωs是光线在无量纲的相合坐标系下的角速度[11]，笔者视ωs为一常数.

太阳帆力学模型的相关参数详见表 1，详见文献[12]，太阳帆受到光压加速度为：

a=aa+ar+ath. (4)

2 动力学系统

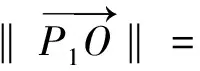
图1 圆型限制性三体问题Fig.1 Circular restricted three-body problem

考虑大天体是扁球的情况下，太阳帆在该系统的运动微分方程为：

(5)

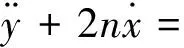
(6)

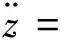
(7)

其中Ω表示势函数，见文献[6].

Ω=n2(x2+y2)/2+(1-μ)/r1+μ/r2+

(1-μ)A1/2/r13-3(1-μ)A1z2/2/r15.

(8)

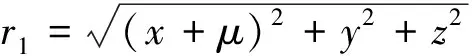
ax=a0[f(p,α)+g(p,α)]cos (ωst)；

(9)

ay=-a0[f(p,α)+g(p,α)]sin (ωst)；

(10)

az=a0h(p,α)，

(11)

式中，f(·)、g(·)、h(·)是p和α的函数.

f(p,α)=(1-p)(1.654 4cos2α+

0.041 7cosα-0.827 2)cosα;

(12)

g(p,α)=p(1-0.052 6cosα)cosα;

(13)

h(p,α)= (1.654 4cosα-1.654 4pcosα-

0.094 3p+0.041 7)sinαcosα.

(14)

运用文献[14]中提到的方法，即把原点移动到小天体并进行坐标变换：

x=1-μ+μ1/3X;y=μ1/3Y;z=μ1/3Z.

(15)

令μ→0，则含扁率的希尔型限制性三体问题可以表示为：

(16)

(17)

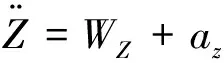
(18)

式中:W为新系统的势函数.

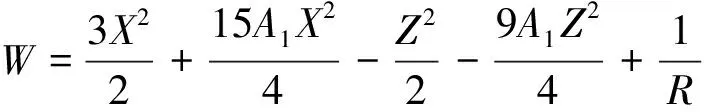
(19)

(20)

3 共线平衡点

求解以下方程组可以得到系统的平衡点：

WX+ax=0；

(21)

WY+ay=0；

(22)

WZ+az=0.

(23)

经典的希尔型三体问题只有两个对称的共线平衡点，笔者主要研究希尔型三体系统的共线平衡点和其附近邻域的轨道运动情况.假设该系统的L1、L2两共线平衡点位于X轴上，用Re=(Xe,0,0)T表示共线平衡点.很显然共线平衡点满足式(21)、(22)和(23)，整理可以得到：

3Xe+ 15A1Xe/2-Xe/Xe3+
a0[f(p,α)+g(p,α)]=0;

(24)

-a0[f(p,α)+g(p,α)]sin(ωst)=0;

(25)

a0h(p,α)=0.

(26)

α=0,ωst=2kπ(k∈Ζ)是式(25)和(26)成立的必要条件，把其代入式(24)，观察式(24)，发现共线平衡点的位置由p、a0和A1共同决定.运用类似文献[15]的数值计算方法，在3个参数p、a0、A1当中，固定一个参数不变，然后观察其他两个参数变化对共线平衡点位置的影响.图2表示的是，当太阳帆特征加速度为一常值时，参数p和A1的改变对L1、L2位置的影响.经典的希尔型限制性三体问题的共线平衡点位置为X=±3-1/3≈±0.693 361 ，然而含扁率的希尔系统的L1的横坐标最小值为-0.693 459 ，L2的最大值为0.693 264.然后，按照同样的方法，固定一个参数，设定扁率A1为一个常数，A1=0.004 23，则共线平衡点位置变化显示在图3.

图2 含扁率的希尔系统共线平衡点位置变化图，a0=0.001,p∈[0,0.125],A1∈[0,1] Fig.2 Positions of collinear equilibrium points in the Hill’s system with oblateness with variational p and A1 with fixed a0=0.001 ，p∈[0,0.125]，A1∈[0,1]

图3 含扁率的希尔系统共线平衡点位置变化图，A1=0.004 23,p∈[0,0.125],a0∈[0,1] Fig.3 Positions of collinear equilibrium points in the Hill’s system with oblateness with variational p and a0 with fixed A1=0.004 23, p∈[0,0.125]，a0∈[0,1]

4 系统线性化

为了更进一步研究太阳帆轨道，需要对系统微分方程进行线性化处理，即在平衡点处引入小的扰动，然后利用泰勒展开式，略去对系统影响很小的高阶项，只保留线性项，建立变分方程.于是，在平衡点引入小扰动：

X=Xe+ξ,Y=η,Z=ζ.

(27)

然后把小扰动代入到系统方程，再进行线性化处理就可得到变分方程：

ξ+uξ；

(28)

(29)

(30)

其中，

WXX=3X2/R5-1/R3+3.0375；

(31)

WYY=3Y2/R5-1/R3；

(32)

WZZ=3Z2/R5-1/R3-1.0225；

(33)

u=[uξ,uη,uζ]T=[ax,ay,az]T.

(34)

此处的Wije(i,j=X,Y,Z)表示势函数的二阶偏导数在共线平衡点的取值，可以把变分方程写成状态空间的矩阵方程：

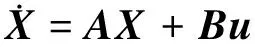
(35)

(36)

5 仿真计算

5.1 追踪参考轨道

求解共线平衡点附近的太阳帆悬浮轨道，运用Simo[11]提出的方法，引入参考轨道：

ξref=ξ0cos (ωst)；

(37)

ηref=η0sin (ωst)；

(38)

ζref=ζ0.

(39)

参考轨道满足系统变分方程，把参考轨道代入式(28)～式(30)，从而得到:

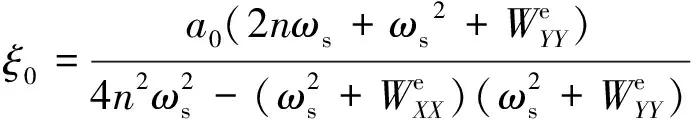
[f(p,α)+g(p,α)];

(40)

[f(p,α)+g(p,α)];

(41)

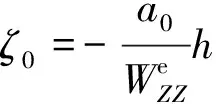
(42)

确定了参考轨道，就可以利用线性二次调节器(LQR)对太阳帆进行主动控制，从而控制太阳帆追踪给定的参考轨道Xref=(ξref,ηref,ζref)T，主动控制可以使太阳帆轨道趋于渐近稳定.考虑太阳帆轨道与参考轨道之间的误差ΔX=X-Xref，然后应用线性反馈控制，Δu=u-uref=-K(X-Xref)，使误差ΔX满足性能指标函数J取最小值：

ΔXTQΔX+ΔuTRΔu)dt.

(43)

其中,Q和R为系统的加权矩阵，是对称正定或半正定的，可以自由选择.通过求解代数黎卡提方程(Algebraic Riccati Equation)，见文献[16]：

ATP+PA-PBR-1BTP+Q=0,

(44)

可以获得收益矩阵K=R-1BTP，这样就把非线性系统(35)转化为稳定的线性系统:

(45)

判断太阳帆轨道是否稳定取决于矩阵A-BK特征值的实部是否是小于或等于0.表 2给出系统的相关参数和仿真的初始条件，这些参数的选取可根据具体的任务要求而确定，具有任意性.

表2 系统参数和仿真初始条件

5.2 仿真计算

通过仿真计算，可以求出理想太阳帆模型下共线平衡点L1的横坐标位置-0.693 361 274 35.图 4表示的是在主动控制下太阳帆周期悬浮轨道，可以看出太阳帆从扰动点出发，通过主动控制，逐渐接近参考轨道，最终几乎与参考轨道重合，图 5给出悬浮轨道与参考轨道的相对位置与速度误差，最大位置误差为2.947 68×10-5，最大的速度误差为7.464 65×10-5，当轨道趋于渐近稳定后，位置误差保持在10-8左右，速度误差保持在10-15左右.仿真结果表明通过追踪参考轨道而设计出来的悬浮轨道可以达到渐近稳定的状态.

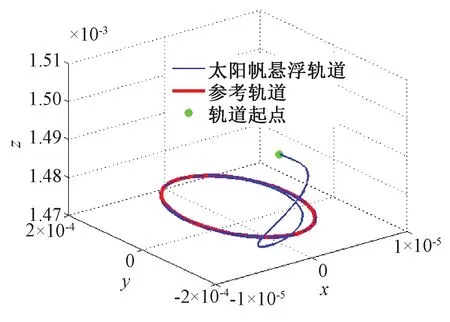
图4 太阳帆悬浮轨道Fig.4 Solar sail displaced orbit

太阳光压加速度沿三轴的分量随时间的变化情况见图6.可以看出,太阳光压加速度在三轴的分量以x轴变化幅度最大，y轴的变化次之，z轴的变化幅度最小，而且沿x,y两轴的加速度分量变化具有周期性：x轴的加速度最大值为3.404 9×10-4，最小值为-3.404 8×10-4；y轴的加速度最大值为3.415 7×10-4，最小值为-6.401 1×10-4；z轴的光压加速度大致在区间[0.005 920,0.005 958]小幅度变化，在太阳帆运行大概4.7个单位时间后，沿该轴的加速度趋于平稳，稳定在0.005 931附近.图 7表示的是RCD控制参数p和太阳帆姿态角α随时间的变化图.由图可以看出，两个变化的参数都是在开始的一段时间大幅度变化，之后进入平稳期，参数p最终稳定在0.202附近，而姿态角α最终稳定在44.99°左右，这也表明两个参数最终稳定值取决于参考轨道的对应参数值.

图5 太阳帆悬浮轨道和参考轨道间的相对位置误差和相对速度误差Fig.5 Relative position error and velocity error between solar sail displaced orbit and refer orbit

图6 太阳帆光压加速度Fig.6 Solar radiation pressure acceleration

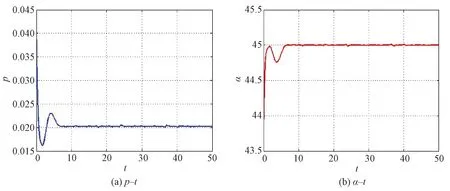
图7 RCD控制参数p和太阳帆姿态角α随时间变化图Fig.7 Time histories of control parameter of RCD and the pitch angle of the solar sail

6 结论

在考虑大天体含扁率的情况下，研究了太阳帆在希尔型限制性三体问题的悬浮轨道设计方案，并利用近似简化，建立太阳帆在希尔型限制性三体问题系统中的动力学模型.研究发现，改变反射控制设备中吸收光线模块和热辐射模块的面积大小；或者改变太阳帆特征加速度；或者改变大天体扁率都会引起系统的共线平衡点的位置发生变化.对系统进行了线性化处理，运用LQR对不稳定的系统进行主动控制.通过调节太阳帆姿态角和改变吸收光线模块的面积可以得到太阳帆悬浮轨道并且使其达到渐近稳定.

参考文献：

[1] TSUDA Y, MORI O, FUNASE R, et al. Flight status of IKAROS deep space solar sail demonstrator [J]. Acta astronaut, 2011, 69(9/10): 833-840.

[2] BAOYIN H, MCINNES C. Solar sail equilibria in the elliptical restricted three-body problem [J]. J Guid Control Dynam, 2006, 29(3): 538-543.

[3] SOSNITSKII S. On the hill stable motions in the three-body problem [J]. Adv Space Res, 2015, 56(5): 859-864.

[4] SHARMA R K. Periodic-orbits of the 3rd kind in the restricted 3-body problem with oblateness [J]. Astrophys & space scicence, 1990, 166(2): 211-218.

[5] SINGH J. Combined effects of oblateness and radiation on the nonlinear stability of L4 in the restricted three-body problem [J]. Astron J, 2009, 137(2): 3286-3292.

[6] DOUSKOS C N, MARKELLOS V V. Out-of-plane equilibrium points in the restricted three-body problem with oblateness [J]. Astronomy and astrophysics, 2006, 446(1): 357-360.

[7] TSUDA Y, MORI O, FUNASE R, et al. Achievement of IKAROS - Japanese deep space solar sail demonstration mission [J]. Acta astronaut, 2013, 82(2): 183-188.

[8] MU J S, GONG S P, LI J F. Reflectivity-controlled solar sail formation flying for magnetosphere mission [J]. Aerosp Sci Technol, 2013, 30(1): 339-348.

[9] GONG S P, LI J F, SIMO J. Orbital motions of a solar sail around the L2earth-moon libration point [J]. Journal of guidance, control, and dynamics, 2014, 37(4): 1349-1356.

[10] GONG S P, LI J F. Equilibria near asteroids for solar sails with reflection control devices [J]. Astrophys & space science, 2015, 355(2): 213-223.

[11] SIMO J, MCINNES C. Solar sail orbits at the Earth-Moon libration points [J]. Commun nonlinear scicence, 2009, 14(12): 4191-4196.

[12] MCINNES C R. Solar sailing: technology, dynamics and mission applications[M]. London: Springer, 1999.

[13] SHARMA R K, RAO P V S. A case of commensurability induced by oblateness [J]. Celestial mechanics and dynamical astronomy, 1978, 18(2): 185-194.

[14] MARKELLOS V V, ROY A E, PERDIOS E A, et al. A hill problem with oblate primaries and effect of oblateness on hill stability of orbits [J]. Astrophys & space science, 2001, 278(3): 295-304.

[15] TSIROGIANNIS G A, DOUSKOS C N, PERDIOS E A. Computation of the Liapunov orbits in the photogravitational RTBP with oblateness [J]. Astrophys & space science, 2006, 305(4): 389-398.

[16] WIE B. Space vehicle dynamics and control[J]. Aircraft engineering and oerospace technology, 1998,70(5): 2077-2078.