广东省雷州市第八中学(524232) 魏欣 邓春梅

本文对2017年高考课标卷III理科第21题进行分析,给出了多种思路和解法,并总结出本题的命题背景和高考中常考的经典函数.

一、原题展示

(2017年高考课标卷III理科第 21题)已知函数f(x)=x−1−alnx.

(I)若f(x)≥0,求a的值;

二、试题分析

本题考查了函数的单调性、最值、数列不等式恒成立问题.以含参数不等式问题为载体,既考查学生的分类讨论思想、等价转化思想、数形结合思想和函数方程以及不等式思想,又考查学生分析问题和解决问题的能力.

三、解法探究

对于第(I)问,在函数的所有问题中,函数单调性是最基础的问题,也是所有问题的思考起点.若含有参数,一般应对参数进行讨论,从而确定函数的单调性,再根据所求进行相应的判断与证明.

思路一通过对导函数进行探究,确定原函数的单调区间,同时还应对参数a进行讨论,解题关键是利用f(x)≥0对a的范围进行取舍.

解法一因为函数f(x)=x−1−alnx的定义域为(0,+∞),则,且f(1)=0.

当a≤0时,f′(x)＞0,f(x)在(0,+∞)上单调递增,所以当0＜x＜1时,f(x)＜0,不满足题意;

当a＞0时,当0＜ x＜ a时,f′(x)＜ 0,则f(x)在(0,a)上单调递减;当x＞a时,f′(x)＞ 0,则f(x)在(a,+∞)上单调递增.

①若a＜1,则f(x)在(a,1)上单调递增,所以当x∈(a,1)时,f(x)＜f(1)=0,矛盾;

②若a＞1,则f(x)在(1,a)上单调递减,所以x∈(1,a)时,f(x)＜f(1)=0,矛盾;

③若a=1,则f(x)在(0,1)上单调递减,则f(x)在(1,+∞)上单调递增,所以f(x)min=f(1)=0.所以f(x)≥f(1)=0满足题意.

综上所述,a=1.

思路二本题先通过研究导函数的正负,确定f(x)的单调区间,求出函数f(x)的最小值,由最小值的范围来确定a的取值范围.

解法二

当a≤ 0时,f′(x)≥ 0,x→ 0+时,f(x)→ −∞,这与f(x)≥0矛盾;

当a＞0时,f(x)在(0,a)上单调递减,在(a,+∞)上单调递增;f(x)min=f(a)=a−1−alna.令g(a)=a−1−alna(a ＞ 0),则 g′(a)= −lna,当 a ∈ (0,1),g′(a)＞ 0,所以g(a)在(0,1)上单调递增,当a∈(1,+∞),g′(a)＜ 0,所以g(a)在(1,+∞)上单调递减.所以g(a)max=g(1)=0,即g(a)≤0.因此当a=1时,f(x)min=0,满足f(x)≥0.所以a=1.

思路三本题注意通过求函数的导数,对函数单调性进行研究,求解函数最小值点即可,运用此种方法应该注意“f(1)=0”在解题中的作用.

解法三因为函数f(x)=x−1−alnx的定义域为(0,+∞).

思路四本题可以根据以往的解题经验,利用结论“lnx≤x−1”和数形结合,这样可以避免复杂的运算,同时也揭示了代数问题的几何背景.

解法四联想lnx≤x−1,可以将不等式f(x)=x−1−alnx≥0转化为.我们可以考察直线与函数y=lnx图像,当a=1时,直线的图像与曲线y=lnx的图像相切于点(1,0).此时f(x)≥0恒成立,故a=1满足条件.

对于第(II)问,数列与不等式的证明主要有以下常规思路:首先,通过函数的单调性得到数列的单调性,从而解决问题;其次,对数列的不等关系进行放缩,直接证明.

思路一本题常规思路是将问题转化为“和”式不等式,根据数列求和求解,但需要将不等式左边放大,可尝试使用不等式ln(x+1)≤x进行放缩.

解法一当a=1时,f(x)=x−1−lnx≥ 0,即lnx≤x−1,则有ln(x+1)≤x,当且仅当x=0时等号成立.所以.一方面,

思路二本题也可逆向考虑,先证明,然后在利用不等式ln(x+1)≤x进行放缩.

解法二当a=1时,f(x)=x−1−lnx≥ 0,即lnx≤x−1,则有ln(x+1)≤x,当且仅当x=0时等号成立.逆用求和公式有

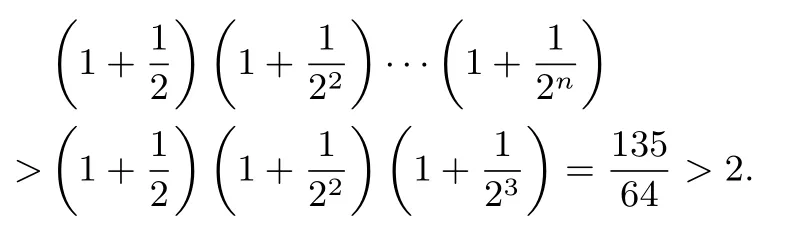
思路三由本题特征不等式的结构特征,也可以尝试用贝努利不等式“(x+1)n≥1+nx,x∈(−1,+∞)”进行放缩.异曲同工,令人赏心悦目,这种“高屋建瓴”的解题思路体现了较高的思维品质.

解法三第(II)问主要证明

事实上,我们注意到1+2a＜ (1+a)2,···,1+2na＜(1+a)2n,联想贝努利不等式的一般形式:(x+1)n≥1+nx,x∈(−1,+∞),于是将代入即可,

另一方面,

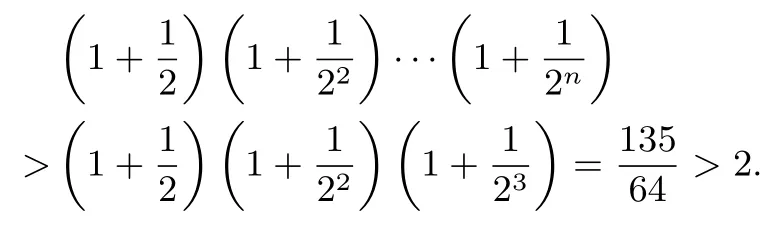
思路四本题除了使用结论ln(x+1)≤x和贝努(利不等式,还可以)尝试用均值不等式C1C2···Cn≤进行放缩.

解法四第(II)问主要证明

由均值不等式得

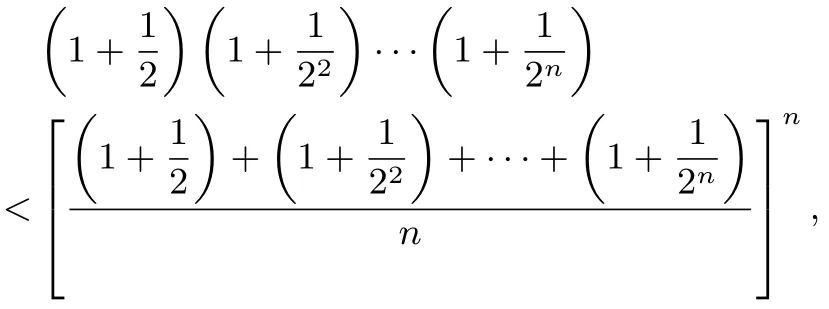
即

又

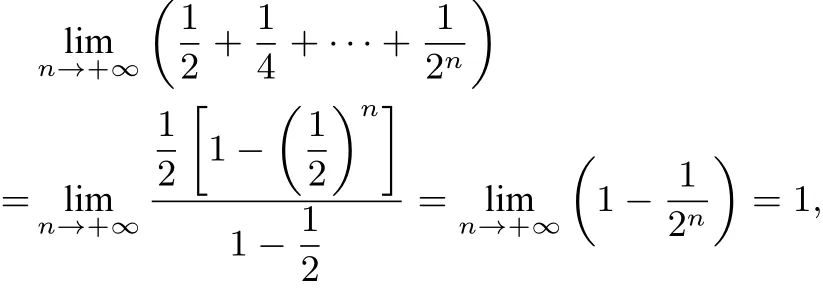
所以

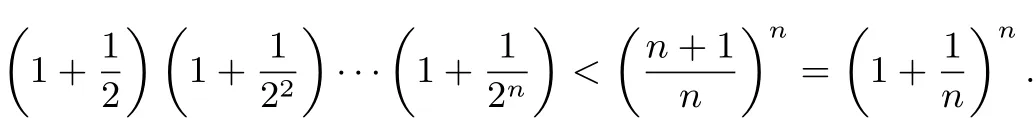
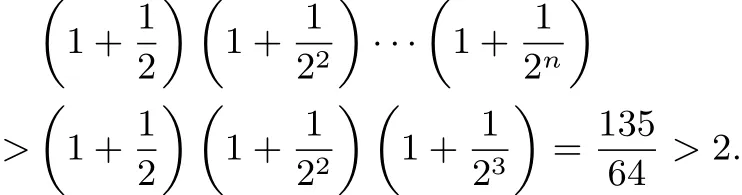
四、解法启发

根据以上解法我们可以看出,第(I)问实质上是考查对不等式lnx≤x−1(x＞0)的几何意义的理解,即从函数的切线寻找解题的突破口.

对于不等式lnx≤x−1(x＞0)深刻理解,经过变形可以得到下面几个结论.

作替换x→ x+1,lnx≤x−1(x＞0)变形为:ln(x+1)≤x(x＞−1).

根据指数式和对数式互化,可得:x+1≤ex(x∈R).

以上式子正是普通高中课程标准实验教科书《数学•选修2-2•A版》(人民教育出版社,2007年1月第2版)第32页习题1.3.B第1(3)题,利用函数的单调性,证明不等式x+1≤ex(x/=0).

这个不等式的证明比较容易,只需构造函数f(x)=ex−x−1(x∈ R),由f′(x)=ex−1知,当x＜ 0时,f′(x)＜ 0;当 x ＞ 0时,f′(x)＞ 0.所以 f(x)在 (−∞,0)上单调递减,f(x)在(0,+∞)上单调递增.故当x=0时,f(x)min=f(0)=e0−0−1=0.即当x∈R时,f(0)≤f(x),也即ex−x−1≥0,故x+1≤ex(x∈R),当且仅当x=0时,等号成立.

在2015年高考福建卷理科第20(1)题,2013年高考全国II卷理科第21(2)题,2010年高考宁夏卷理科第21题等等,也均考查含参不等式恒成立问题,体现了高考试题“常考常新,推陈出新”的理念.均可以用上述的解法解决此类问题,由于篇幅关系,此处不再赘述.

1.(2015年高考福建卷理科第20(1)题)已知函数,f(x)=ln(x+1).证明:当x＞0时,f(x)＜x.

2.(2013年高考全国II卷理科第21(2)题)已知函数f(x)=ex−ln(x+m),证明:当m≤2时,f(x)＞0.

3.(2010年高考宁夏卷理科第21题)设函数f(x)=ex−x−1−ax2.

(I)若a=0,求f(x)的单调区间;

(II)若当x≥0时,f(x)≥0,求a的取值范围.

因为

根据上述证法,我们还可以有如下启发,看来不等式的右边还可以缩小估计数.

因为当k≥2时,

所以

如果上式从第五项开始放大,则

如果上式从第六项开始放大,则

还可以继续下去,如果点破这个问题可以在大学数学分析中圆满解决,则可进一步激发学生的学习欲望.

五、回归教材

在数学教学中,我们要善于挖掘教材的潜在教学功能.教材中有一些典型性题目,它们或者是重要的结论,或者体现某种数学思想方法,或者是某个一般数学命题的具体形式,它的延伸、转化和拓广,可以呈现出丰富多彩的数学内容.我们必须充分重视课本典型例题、习题的探究,这是“用教材教”之根本,也是教师专业成长的必有之路.纵观近几年高考导数压轴题,都考查此类问题,体现了高考试题“常考常新,推陈出新”的理念,所以我们要都这一类问题进行总结,并提出更加简便的通性通法,对解法的探索是在践行我们所学的知识技能和思想方法,同时也使我们的思维更广阔、思想更深刻.对试题本质的探源,使我们更深刻地认识问题,将新旧解题经历跨时空贯通起来,这又是一个新的开始.

[1]魏欣.一道导数高考模拟题的启示[J].中学数学研究.2013(10上):37-39.

[2]魏欣,邓春梅.2017年高考课标卷II文科第21题的待定常数法的解法探究[J].中学数学研究.2017(10上):8-9.

[3]邓军民,魏欣等.高考数学热门考点与解题技巧[M].2017,10.