广东省佛山市顺德区容山中学(528303) 李洪波

高中立体几何中的外接球问题一般综合了多个几何要素,空间位置关系复杂,加上学生对曲面图形的感受性差,是教学中的一个难点．本文通过对比平面图形的外接圆与空间几何体外接球的生成过程,解析外接问题的本质,把空间球的问题“降维”为平面圆的问题来解决,突破外接球问题的难点．

平面上,以三角形的外接圆为例,如图1,在△ABC中,作出其任意两边的垂直平分线,其交点O即为△ABC外接圆的圆心,其中|OA|=|OB|=|OC|,它们均为⊙O的半径．

在空间中,如图2,选取球面上的任意两个小圆(不平行),过其圆心作两个圆面的垂线,这两条垂线的交点即为球心,其中R2=d2+r2．

图1

图2

所以空间中外接球问题就转化为平面内外接圆的问题,其中最重要的就是确定其圆心的位置,再过圆心作圆面的垂线,其交点即为外接球的球心．

我们以下面这个例子来解析一下具体的操作过程:

例1如图3,在菱形ABCD中,将△ABD折起到△PBD的位置(如图4),若二面角,求三棱锥P−BCD的外接球的体积．

图3

图4

解析将二面角P−BD−C放入球中(如图5),圆O1,圆O2分别为两个正三角形的外接圆．由于两个三角形全等,所以它们的外接圆半径相等．由球的性质可知,OO1⊥平面PBD,OO2⊥平面BCD．

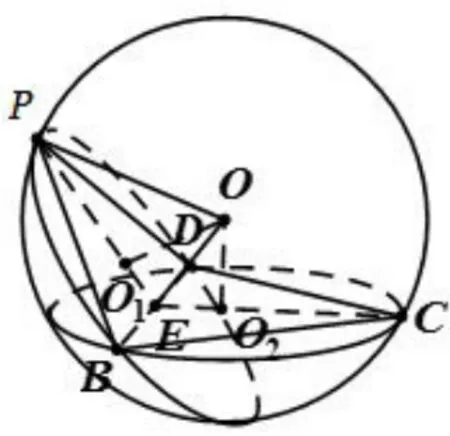
图5

设E为BD中点,由于△PBD,△CBD均为正三角形,所以 PE⊥BD,CE⊥BD,故 ∠PEC即为二面角P−BD−C所成平面角．由对称性可知,∠OEO1=∠OEO2=60°．在正三角形 PBD中,．在 Rt△OO1E中,,所以．在,所以球的体积

下面是几种常见的棱锥外接球问题:

题型1可以补成长方体、正方体

我们常见的平面图形中,正方形,长方形,直角三角形等,它们的外心是很容易确定的,由这几种图形围成的几何体很容易补成长方体或正方体．这样,棱锥的外接球就是长方体或正方体的外接球．由长方体和正方体的对称性可知,它们的体对角线即为外接球的直径,体对角线中点即为球心,这样问题就简单了．

例2已知在直角梯形ABCD中,∠ADC=∠DAB=90°,△ADC与△ABC均为等腰直角三角形,且AD=1,将直角梯形ABCD沿AC折叠成三棱锥D−ABC,当三棱锥D−ABC的体积取得最大值时,求其外接球的表面积．

解析由题意作出直角梯形ABCD如图6,当平面ADC⊥与平面ABC时,三棱锥D−ABC的体积最大(如图7)．此时可以将三棱锥补成长方体(如图8),长方体的长、宽、高分别为,其体对角线即为外接球的直径,所以,故其外接球的表面积S=4πR2=4π．

图6

图7

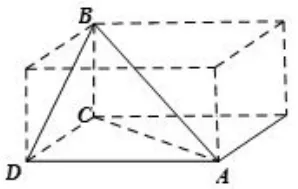
图8

另外,常见的可以补成长方体或正方体的棱锥如下:

题型2正棱锥

正棱锥是立体几何中常见的一种线面角关系的载体,它的外接球问题也是经常出现．

例3一个所有棱长均为1的正四棱锥的顶点与底面的四个顶点均在某个球的球面上,求此球的体积．

解法1设正四棱锥的底面中心为O1,外接球的球心为O,如图9所示,选择两个图形:

图9

(1)正方形ABCD.

由正方形性质可知,O1为底面正方形ABCD外接圆的圆心,由于SO1⊥平面ABCD,故球心O必在SO1所在的直线上.

(2)△SBD.

本例中选择的两个图形可以是棱锥的任何侧面或底面,但在实际解题过程中,我们一般选择一些特殊的的图形,如正方形,长方形,正三角形,等腰三角形,直角三角形等,它们的外心是比较容易确定的．

当然,即使是等腰三角形,想要确定其外心有时也是不容易的,所以解法1可以改进如下:

解法2同解法1,先确定球心O必在SO1所在的直线上,如图10,在Rt△SO1D 中,在 Rt△OO1D 中,由勾股定理,,即可解出．

图10

由于本例中的△ABD恰好是直角三角形,其外接圆的圆心为斜边中点O1,而对一般三角形,解法一不是很方便;解法二的适用范围更广,对侧面三角形形状要求不高,更具有一般性．

题型3一般类型

例4球O的球面上有四点S,A,B,C,其中O,A,B,C四点共面,△ABC是边长为2的正三角形,面SAB⊥面ABC,求棱锥S−ABC的体积的最大值．

解析如图11,由于O,A,B,C四点共面,所以A,B,C在以O为圆心的大圆圆周上．又面SAB⊥面ABC,所以点S在以O1为圆心,且与⊙O垂直的小圆圆周上,则点S到⊙O所在的平面的最大距离为⊙O1的半径 1,所以．

图11

本题中S点的位置是变化的,它可以在⊙O1的圆周上的任何一个位置(除A,B两点以外)．如果仅有棱锥S−ABC的图像,则很难看出S点在哪里,画出两个小圆衬托一下,位置就一目了然了．

例5高为的四棱锥S−ABCD的底面是边长为1的正方形,点S,B,C,D均在半径为1的同一球面上,求底面ABCD的中心与顶点S之间的距离．

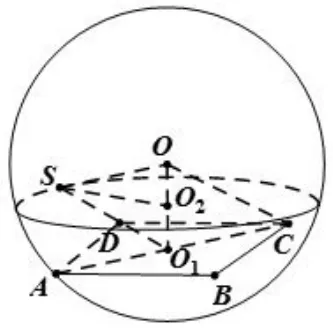
图12

解析如图12,设底面ABCD所在小圆的圆心为O1,则OO1⊥面ABCD．由于棱锥的高为故顶点S在平行于底面ABCD,且与其距离为的⊙O所在平2面上,又因为顶点S也在球面上,故顶点S在⊙O2的圆弧上,且．在Rt△OO1C中,,所以.在 Rt△OO2S中,,所以．在 Rt△O1O2S 中,所以底面ABCD的中心与顶点S之间的距离为1．

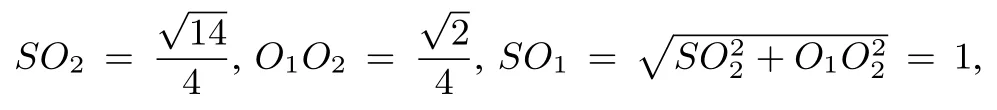
图13

例4与例5的难点都是确定顶点S的位置,一个应用面面垂直,得到两个互相垂直的小圆面,一个应用距离得到两个互相平行的小圆面,有了小圆的参照,位置关系变清晰了．

例6已知三棱锥S−ABC的所有顶点都在球O的球面上,△ABC是边长为1的正三角形,SC为球O的直径,且SC=2,求此棱锥的体积．

解析如图13,OO1⊥平面ABC,SD⊥平面ABC,所以,所以棱锥的高h=SD=2OO1.

本题的关键是确定棱锥的高SD,一开始很多同学想把这个“高”作出来,如果只有一个棱锥的图像,则D点位置的确定很困难,加入了小圆以后,我们发现D点在哪里已经不重要,重要的是SD与OO1的位置关系．

解决球的外接问题,多数时候我们是把几何体从球中拿出来研究,球的作用只是提供几个数据或位置关系,本文的几个例子反其道而行之,把几何体放回去,有了球与小圆衬托,几何体有了根基和背景,再结合求的各种几何性质,这样各种几何要素之间的相对位置关系就会变得容易理解很多．