江苏省锡山高级中学(214174) 陈敏

数学问题的解决就是由已知条件向未知结论的逐步转化,其重点是沟通未知与已知之间的联系,化未知为已知,化陌生为熟悉.事实上,所谓数学核心素养简单地说,就是个体面对复杂的、不确定的新情境时,综合运用已知的数学知识、观念、方法解决问题所表现出来的关键能力与必备品质.数学核心素养是通过一次次解决数学问题逐步培养起来的.但是,问题的难点是如何在新情境下透过现象洞察数学问题的本质,化未知为已知,化陌生为熟悉,挖掘转化条件,从而用已知的数学知识、观念、方法加以解决.解析几何中,直线与圆、圆与圆的位置关系都有明确的等价条件,比较容易解决,但是,在很多情况下这种问题中的圆不是直接告知,而是隐含在题设中,即“隐圆”,需要挖掘转化条件,使之浮出水面.我们可以从圆的定义、圆的方程、圆的性质等方面考虑,挖掘转化条件,使“隐圆”浮出水面.

一、利用圆的定义,使“隐圆”浮出水面

圆的定义平面上到定点的距离等于定长的点的轨迹是圆

例1如图1,圆O:x2+y2=1,圆 M:(x−a)2+(y−a+4)2=1,若圆M上存在点P,过点P作圆O的两条切线,切点为A,B,使得∠APB=60°,则实数a的取值范围是___.

图1

解析由题知在Rt△PAO中,∠APO=30°,OA=1,所以,PO=2,即动点P到定点O的距离是定长2,根据圆的定义,动点P的轨迹是以点O(0,0)为圆心,半径为2的圆,此时“隐圆”浮出水面,又点P在圆M:(x−a)2+(y−a+4)2=1上,进而转化为圆与圆的位置关系:两个圆有公共点,所以,解得.

点评这里利用圆的切线的性质及直角三角形中边角关系得到PO=2,根据圆的定义知道动点P的轨迹是一个圆,使“隐圆”浮出水面,问题转化为熟悉的圆与圆的位置关系问题.

二、利用圆的方程,使“隐圆”浮出水面

圆的标准方程在平面直角坐标系下,以(a,0)为圆心,半径为r(r＞0)圆的标准方程是(x−a)2+(y−b)2=r2.

图2

例2(2016年江苏高考数学第18题改编)如图2,在平面直角坐标系xOy中,已知以M 为圆心的圆M:x2+y2−12x−14y+60=0及其上一点A(2,4),设点T(t,0)满足:存在圆M 上的两点P和Q,使得,求实数t的取值范围.

解析M:x2+y2−12x−14y+60=0的标准方程是M:(x−6)2+(y−7)2=25,设P(x1,y1),Q(x2,y2),因为,又Q(x2,y2)在M上,所以(x2−6)2+(y2−7)2=25,则有[x1−(t+4)]2+(y1−3)2=25,根据圆的标准方程,隐圆[x1−(t+4)]2+(y1−3)2=25就浮出水面,从而P(x1,y1)既在M:(x−6)2+(y−7)2=25上,又在圆[x−(t+4)]2+(y−3)2=25上,进而转化为圆与圆的位置关系:两个圆有公共点,所以,解得.

点评这里把条件坐标化,利用动点转移的方法,结合圆的标准方程形式,使得“隐圆”浮出水面,化归为熟悉的圆与圆的位置关系问题.

例3(2013年江苏高考数学第17题改编)如图3,在平面直角坐标系xOy中,点A(0,3),直线l:y=2x−4.设圆C的半径为1,圆心在l上.若圆C上存在点M,使MA=2MO,求圆心C的横坐标a的取值范围.

综上所述，市政工程绿色施工技术需要施工人员树立绿色环保意识，在施工过程中注意环境保护，节约水资源，避免对周围环境与居民生活造成影响。绿色施工需要合理设计市政工程施工组织、保证施工材料绿色环保、保证市政工程施工环境，控制污染。

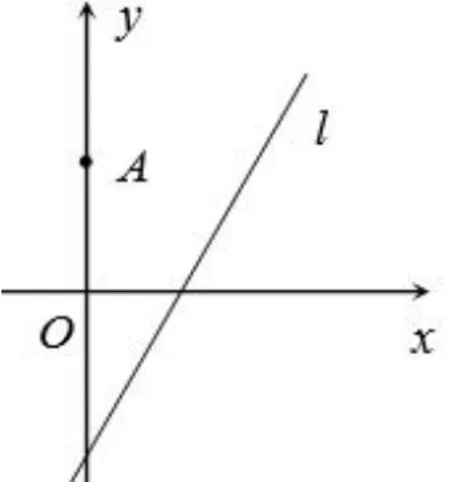
图3

解析由题意可设圆心C(a,2a−4),圆C的方程为(x−a)2+[y−(2a−4)]2=1,设M(x,y),由MA=2MO,得,即 x2+(y+1)2=4,根据圆的标准方程,它表示以(0,−1)为圆心,2为半径的圆,这样隐圆x2+(y+1)2=4就浮出水面,又点M 在圆C上,进而转化为圆与圆的位置关系:两个圆有公共点,所以,解得

点评事实上,在平面上给定相异两点A、B,设P点在同一平面上且满足,当λ＞0且λ/=1时,P点的轨迹是个圆,这个圆我们称作阿波罗尼斯圆.设M、N分别为线段AB按定比λ分割的内分点和外分点,则MN为阿波罗尼斯圆的直径,且.这里 MA=2MO可化为,动点M到两定点A,O的距离之比为一个不等于1的常数,所以动点M的轨迹是一个圆.

例4若等差数列{an}满足,则S=a2015+a2016+a2017+ ···+a4029的最大值是___.

解析设等差数列{an}的公差是d,则,再设m=a1,n=a1+2014d,则m2+n2=,所以

点评通过换元m=a1,n=a1+2014d后,条件转化为,由此联想到圆的标准方程,所求的目标用新元表示后再次换元,发现是直线与圆的关系问题,从而使问题迎刃而解.

三、利用圆的性质,使“隐圆”浮出水面

圆的性质直径所对的圆周角是直角

例5已知实数a,b,c成等差数列,点 P(−1,0)在动直线ax+by+c=0上的投影为M,若N(3,3),求线段MN的最大值.

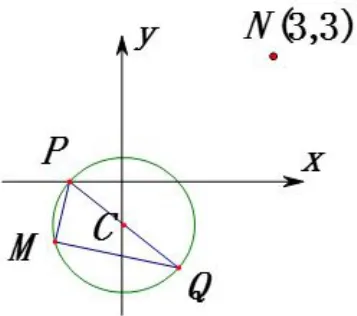
图4

点评解决这道题,首先要发现直线ax+by+c=0过定点Q(1,−2),其次,由于PM⊥MQ,得出点M 对定线段PQ所张的角为90°,根据直径所对的圆周角是直角,发现点M的轨迹是以线段PQ为直径的圆,从而问题转化为熟悉的圆的有关问题.

读者不妨试着从圆的定义、圆的方程、圆的性质等方面考虑,挖掘转化条件,使“隐圆”浮出水面,解决以下问题:

1、如图5,在平面直角坐标系中,已知点B(0,1),A(1,0),点P为线段AB上任意一点,若过点P的直线与以点C(2,2)为圆心,r为半径的圆交于M,N两点且PM=MN,求半径r的最小值.

图5

解析设P(1,1−t),t∈[0,1],M(x,y),则N(2x−t,2y−(1−t)),代入(x−2)2+(y−2)2= r2,得(2x−t−2)2+(2y+t−3)2=r2,即

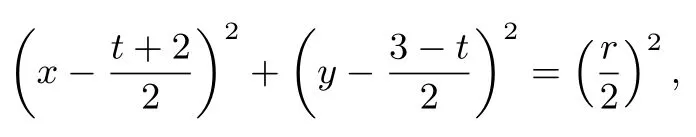
一是代数法,

二是几何法,

2、如图6,在平面直角坐标系中,圆C1:(x−1)2+y2=2,圆C2:(x−m)2+(y+m)2=m2(m ＞0),若圆C2上存在一点P,过点P向圆C1作切线PA,PB,切点为A,B,使得S△PAB=1,求实数m的取值范围.

图6

解析设∠APC1=θ,则所以·,所以,,则.由圆的定义知,P点在以点C1(1,0)为圆心,半径为的“隐圆”上,又点P 在“明圆”C2上,所以这两个圆有公共点,则,解得.

当然,在利用S△PAB=1时,也可以这样,设AB与PC1交于G,PA2=PG·PC1,而,所以

事实上,在求得PC1=2后,也可以不用这里所谓的“隐圆”与“明圆”的方法.因为点P在圆C2上,所以PC1的最小值是的最大值是,所以,解得.