冯春生,　舒　适,　梁文涛

(湘潭大学 数学与计算科学学院，科学工程计算与数值仿真湖南省重点实验室，湖南 湘潭 411105)

弹性力学问题是固体力学中的一种基本模型，它广泛应用于建筑、机械、化工、航天等领域. 有限元方法是求解弹性力学问题的最常用的离散化方法之一.由于有限元方程系数矩阵的条件数会随着网格尺寸的减小而迅速增大，用经典迭代法求解时收敛较慢.因此，研究求解大规模弹性问题有限元离散系统的快速算法非常必要.

非重叠DDM 是为大规模偏微分方程离散系统构造有效并行预条件子的一类非常重要的方法[1-3].标量椭圆方程方面研究工作已比较成熟，[1]针对H(grad)型椭圆问题设计了非重叠DDM 预条件子.非重叠DDM预条件子经过近几十年的发展，先后形成了如BPS型[1]、Neumann型[2]和FETI型[3]等构造预条件子的模式.最近，[4]为标量椭圆问题线性元方程设计了一种基于简单粗空间的非重叠DDM 高效预条件子.多层网格法[5-7]是高效求解规模偏微分方程离散系统的另一类重要方法.代数多层网格(AMG)法诞生于20世纪80年代初[8]，它是求解大规模偏微分方程离散化系统的最为有效的迭代方法之一.20世纪90年代以来，受实际应用问题的驱动，AMG 法得以迅速发展[9-10].目前常用的AMG 法包括经典AMG法(简称C-AMG法)[11]，基于能量极小基的AMG法[12]，自适应AMG法[13]和GAMG 法等，其中GAMG法是指针对不同特性的问题，通过利用其中部分容易获得的几何或分析信息而设计的依赖于问题的AMG 法，如AMGe法[14]和基于光滑聚集的AMG法[15]等.GAMG法由于具有更高的运算效率，已成为当前国际AMG 法研究领域中的热点.

1　线弹性模型问题与线性有限元方程

考虑如下三维线弹性问题：

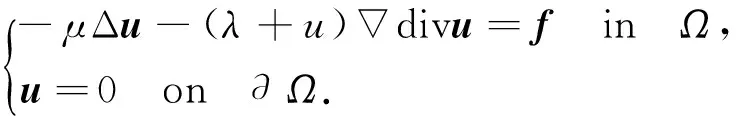
(1)

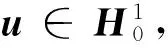
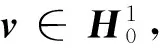
(2)

其中

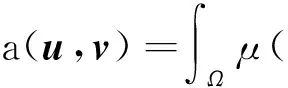
(3)

(4)

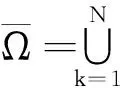
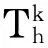
变分问题式(2)的线性有限元近似变分问题为：求uh∈Vh(Ω)，使得

a(uh,vh)=(f,vh),∀vh∈Vh(Ω),

(5)

则式(5)的代数形式为

Au=f.

(6)

下面我们利用代数多层网格法与非重叠DDM预条件子[4]， 为求解式(6)的PCG法构造一种并行预条件子.

2　一种并行预条件子

为了给出方程式(6)中系数矩阵A的一种基于非重叠DDM的预条件行为B的构造算法，只需给出求向量w=Bg的算法， 其中g为任给的已知向量，其计算公式为

(7)

其中，关于求解式(7)右端中的各个向量的算法可描述如算法1 (这里设wd,wW,wl,g分别为以wd,wW,wl和g的分量为自由度的线性有限元函数)：

算法1非重叠DDM的预条件子

(1) 求wd∈Vd(Ω)，满足如下变分子问题：

a(wd,vd)=(g,vd),∀vd∈Vd(Ω).

(8)

(2) 求wW∈VW(Ω)，满足如下变分子问题：

a(wW,vW)=(g,vW),∀vW∈VW(Ω).

(9)

(3) 对内交界面循环，设当前交界面号为l(它对应内交界面Γij)，求wl∈Vl(Ωij)，满足如下变分子问题：

a(wl,vl)=(g,vl),∀vl∈Vl(Ωij).

(10)

第一类子系统式(8)：由于其自由度较少，使用经典迭代法CG 或C-AMG都可求解；第二类子系统式(9)：由于其系数矩阵性态较好，使用CG求解即可；第三类子系统式(10)：每个内界面对应一个，此类子问题求解性态的好坏，将直接影响整个预条件子系统求解的效率.针对第三类子系统式(10)的求解，研究发现随着子系统规模的增大，使用经典迭代法如CG求解时，迭代次数随子问题规模的扩大增长很快，而使用C-AMG求解该类子系统时，迭代次数不稳定，且求解效率较低.因此，需要设计新的高效AMG 法.特别地，通过改变C-AMG 中的粗化策略和提升算子的构造方法，我们为第三类子系统设计了一种新的AMG (简记为AMG-T)法.

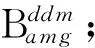
3　并行实现

记Ad:Vd(Ω)→Vd(Ω)，AW:VW(Ω)→VW(Ω) 和Al：Vl(Ωij)→Vl(Ωij)为三个对称正定算子；记Qd，QW和Ql分别表示Vh(Ω) 到相应子空间Vd(Ω)，VW(Ω)和Vl(Ωij)的L2投影算子.记变分子问题式(8)、(9)、(10)对应的离散系统分别为:

Adud=Qdg，

(11)

AWuW=QWg，

(12)

Alul=Qlg.

(13)

这里，在不与算子Ad,AW,Al产生混淆的情况下，记其对应的矩阵为Ad,AW,Al(l=1,…,M).

接下来，针对AW规模较大，且子系统式(13) 的求解占主要工作量的情形简要给出MPI + OpenMP二级并行实现策略.关于第一类子系统式(11)：由于其自由度较少, 通常可以在第0#进程上采用BoomerAMG[16]进行OpenMP 并行求解.如果直接调用BoomerAMG,求解效率不够理想，可以采用我们新设计的一种解法器AMG-T(与前者不同之处在于粗化策略考虑方向性).由表1可知, 当md较大时，AMG-T的迭代次数比较稳定.

关于第二类子系统式(12)：由于其系数矩阵性态较好，调用OpenMP 并行CG在第1#进程上求解即可.由表2可知，并行CG的迭代次数与网格规模和进程数均无关.

关于第三类子系统式(13)，注意以下两个事实：

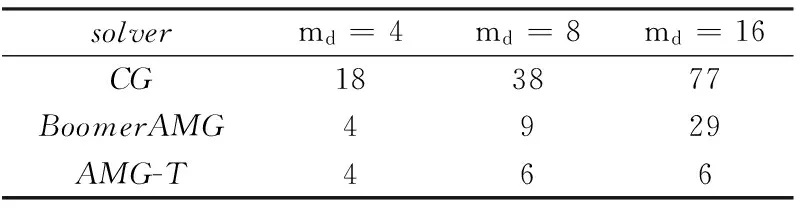
表1　求解第一类子系统(11)的平均迭代次数

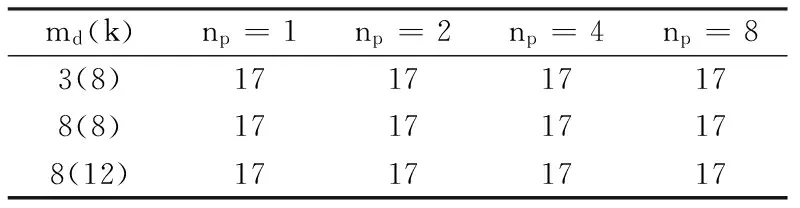
表2　并行 CG 求解第二类子系统(12)的迭代次数

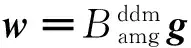
事实2该类子系统的求解可同步进行，且可自由组合聚集到不同进程并行计算.

因此，我们将第三类子系统平衡分配到余下进程并行计算.进一步，在各进程上将分配到该进程上的第三类子系统再平均分配到各线程上，采用OpenMP并行求解.

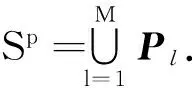
(14)

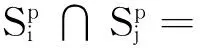
(15)

|Ni-Nj|≤1, |Ni, l-Ni, m|≤1, ∀i≠j,∀l≠m.

(16)

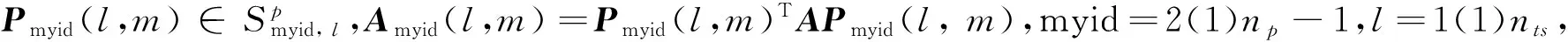
m=1(1)Nmyid, l,分别表示第myid号进程上的第l个线程上的第m个转换算子对应的矩阵和相应子系统的系数矩阵.

算法2MPI+OpenMP并行非重叠DDM的预条件子

Step 1初始化并行向量z.

Step 2将并行向量r转为串行向量， 不妨仍记为r.

Step 3若myid=0，则zmyid:= (PdTBdPd)r；

若myid=1， 则zmyid:= (PWTBWPW)r；

若myid≠0 且myid≠1并行做以下循环

form=1,…,nts

Step 3.1求Ft(l,m):=Pmyid(l,m)r.

Step 3.2求yt(l,m)=Bmyid(l,m)Ft(l,m)

Step 3.3求zmyid:=zmyid+(Pmyid(l,m))Tyt(l,m).

end for

注1若子问题规模 (存储规模) 能由一个计算结点容纳时，子问题求解调用HYPRE[16]中串行AMG 或AMG-T；否则，当子问题规模超过一个计算结点的容纳能力时，子问题求解调用HYPRE中并行AMG或并行AMG-T求解.本文数值实验部分的子问题求解调用HYPRE中的串行AMG 或AMG-T.

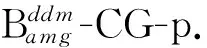
4　数值实验

在线弹性模型问题式(1)中， 取单位立方体Ω:=(0,1)×(0,1)×(0,1)；E=3 000,v=

0.3；f=(f1,f2,f3)T， 其中

f1(x,y,z)=(λ+4μ)π2sin(πx)sin(πy)sin(πz)-(λ+μ)(3x2-4x3)πcos(πy)sin(πz)-

(λ+μ)π2y3(1-y)cos(πx)cos(πz),

f2(x,y,z)=-(λ+μ)π2cos(πx)cos(πy)sin(πz)-(λ+μ)(3y2-4y3)πsin(πx)cos(πz)+

[(12x2-6x)μ+π2x3(1-x)(λ+3μ)]sin(πy)sin(πz),

f3(x,y,z)=(λ+μ)π2cos(πx)sin(πy)cos(πz)-(λ+μ)π2x3(1-x)cos(πx)cos(πz)+

[(12y2-6y)μ+π2y3(1-y)(λ+3μ)]sin(πx)sin(πz).

数值实验硬件环境为某2路4核工作站(CPU： Intel Xeon W5590*2， Mem：24 GB)； 软件环境为Linux Redhat 5.3，gcc v4.1.2，gfortran v4.1.2，mpich2-1.3.2p1，hypre-2.7.0b.由于该工作站总共只有8 个核,因此我们只针对进程数和线程数不大于8 的情形进行数值实验，这样可以保证进程或线程与核一一对应.实验中取PCG迭代控制精度为10-6.

算法可扩展性表4给出了不同网格剖分Τmd,k和不同进程数np下PCG算法的外迭代次数.

由表4可知，当d/h不变时，条件数κ(BA) 为常量，表明该预条件子的算法可扩展性达到最优；当d不变，h变小时，条件数κ(BA) 仅弱依赖于d/h=k.

第三类子系统的并行可扩展性表5给出了相应的CPU时间与并行效率.

由表5可知，当进程数np=8 时加速比达到95%以上而未达到100%.可能的原因为：负载不够平衡.可以预测，在更多进程参与计算的情况下，该类子问题的求解加速性能不差.若进程数足够多，该类子问题的求解时间将大幅下降.

表4　不同Τmd,k与np下PCG的外迭代次数

表5　不同Τmd,k与np下求解第三类子系统的CPU时间与并行效率

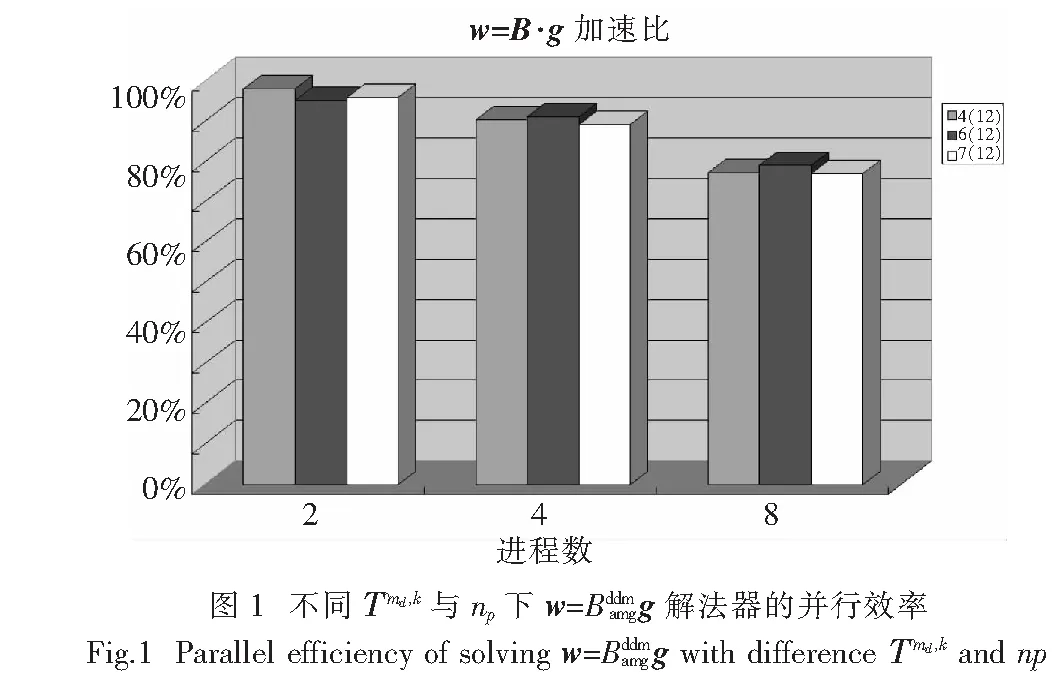
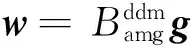
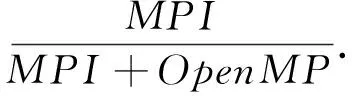
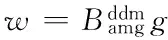
表6　在不同并行模式下求解的时间比值

实验结果表明在曙光5000上求解该DDM预条件系统时，采用MPI+OpenMP 模式比MPI模式计算效率更高.

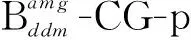
感谢湘潭大学王俊仙博士在并行DDM 算法设计方面提供的良好建议.

[1]DRYJA M, SMITH F,WIDLUND O.Schwarz analysis of iterative substructuring algorithms for elliptic problems in three dimensions[J].SIAM J Numer Anal, 1994,31(6):1662-1694.

[2]DRYJA M,WIDLUND O. Schwarz methods of neumann type for three-dimensional elliptic finite element problems[J].Comm Pure Appl Math, 1995, 48:121-155.

[3]HU Q,SHI Z,YU D.Efficient solvers for saddle point problems arising from domain decompositions with lagrange multipliers[J].SIAM J Numer Anal, 2004,42(3):905-933.

[4]HU Q,SHU S,WANG J.Nonoverlapping domain decomposition methods with simplified coarse spaces for solving three-dimensional elliptic problems[J].Math Comp, 2010, 79(272): 2059-2078.

[5]FENG C,SHU S, XU J,et al.Numerical study of geometric multigrid methods on CPU-GPU heterogeneous computers[J].AAMM, 2014, 6(1):1-23.

[6]FENG C,ZHANG S.Optimal solver for morley element discretization of biharmonic equation on shape-regular grids[J].JCM, 2016, 34(2):159-173.

[7]谭林, 江军, 舒适, 一种三角形网格下保对称有限体元方法的预条件技术[J].湘潭大学自然科学学报, 2006,28(1):1-6.

[8]BRANDT A, MCCORMICK S,RUGE J.Algebraic multigrid (AMG) for automatic multigrid solution with application to geodetic computations[P].Institute for Computational Studies, POB 1852, Fort Collins, Colorado, 1982.

[9]STERCK H D,YANG U M,HEYS J J.Reducing complextity in parallel algebraic multigrid preconditioners[J].SIAM J Mat Anal Appl,2006,27(4):1019-1039.

[10]BIENZ A,FALGOUT R D,GROPP W,et al.Reducing parallel communication in algebraic multigrid through sparsification[J].SIAM J Sci Comp, 2016, 38(5): S332-S357.

[11]RUGE J W, STüBEN K. Algebraic multigrid[M]//Multigrid Methods.Philadelphia:SIAM,1987:73-130.

[12]XU J,ZIKATANOV L.On the energy minimizing base for algebraic multigrid methods[J].Computing and Visualization in Science, 2004, 7:121-127.

[13]BREZINA M,FALGOUT R D,MACLACHLAN S,et al.Addaptive smoothed aggregation(αSA)[J].SIAM Review, 2005, 47(2):317-346.

[14]CHARTIER T,FALGOUT R D,HENSON V E,et al.Spectral AMGe(ρAMGe)[J].SIAM J Sci Comp,2003,20(1):1-20.

[15]VANEK P,MANDEL J,BREZINA M.Algebraic multigrid by smoothedaggregation for second and fourth order elliptic problems[J].Computing, 1996, 56:179-196.

[16]赵永华, 迟学斌.基于SMP集群的MPI+OpenMP混合编程模型及有效实现[J].微电子学与计算机,2005,22(10):7-11.

[17]FALGOUT R D,BAKER A,CHOW E,et al.HYPRE: High performance preconditioner[OL].https://computation.llnl.gov/casc/hypre/software.html.