张　媛

(重庆邮电大学 移通学院，重庆 401520)

随着控制技术的快速发展，专家对控制系统的实时性和全局稳定性提出更高的要求.非光滑自治时滞控制系统是一个多变量、非线性的齐次耦合控制系统，该类控制系统在时滞控制、滑模控制、积分控制等方面具有很好的全局调控能力[1]，从而广泛应用在数学、力学和物理学方面的控制器设计中，在航空航天、船舶、人工智能等领域就有很好的应用前景.

研究非线性奇摄动方程，可以描述具有时滞控制系统的全局稳定性、渐进收敛性和鲁棒性等问题，避免传统的齐次渐进展开方法不具有鲁棒性的缺点[2-3].对此，本文研究了非线性奇摄动边值解向量的零次渐近展开式收敛性和稳定性问题.

1　问题描述和相关定理

1.1　非线性奇摄动方程

本文研究非线性奇摄动边值问题的零次渐近展开式的稳定性和渐进收敛性问题，为非光滑自治时滞控制系统提供理论支持，建立一类具有齐次双曲波动扰动项的非线性奇摄动方程如下：

(1)

式中，u:I×Rd→R是连续二自由度函数，d≥4，0∈I⊂R是上下边界区间.设摄动方程的随机凸函数为[4，5]：

采用连续多元映射uuλ将(1)进行高阶时频分解，得到非线性奇摄动的连续马尔尼数链：

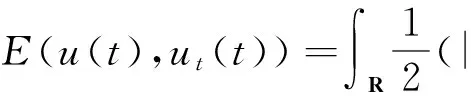
1.2　相关定义与定理

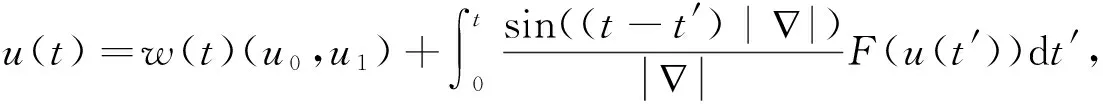
其中F(u)= |u|4u.

设x*是解集{xk}中的一个极限点，方程的连续奇异分解算子w(t)(u0,u1)=cos(t||)是摄动方程在满足边界稳定条件为(u0,u1)时的解.采用微分双曲方程构建非线性奇摄动系统模型为：

x(k+1)=Ax(k)+Bu(k)，z(k)=Cx(k)，

其中x(k)∈Rp表示非线性奇摄输入状态项，u(k)∈Rq表示不确定时延输入，z(k)∈Rm表示边界解向量的输出,A,B,C为适当维数矩阵，变量p,q,m为正整数.在不确定时延和高阶扰动下，根据广义Lyapunove稳定性原理[7]，非线性奇摄动系统受到的未知扰动为：

式中：x(t)=[x1(t),x2(t),…,xt(t)]T是在时滞变量为t的状态向量，d1(t)和d2(t)分别表示未知的建模误差和未知的扰动泛函.定义摄动边值有限能量项d(t)=d1(t)+d2(t).在超临界条件下，对方程进行边值稳定性求解，构造传递函数：

在边值稳定条件下，对于给定的正常数γ，如果满足FTF≤I，得到方程的非线性项为|u|4/(d-2)u，摄动过程用utt-Δu+|u|pu=0,(p>4)表示，在奇异空间R3中通过渐进展开方式进行系统闭环控制，满足零次渐进展开的整体收敛性(定理1).

Ψ(h1,h2)=Ψ+h1K(Z1+Z2+Z3)-1KT+h2M(Z2+Z3)-1MT<0.

得到：

Ψ(h1,0)=Ψ+h1K(Z1+Z2+Z3)-1KT+h2L(Z2+Z3)-1LT<0

Ψ(0,h2)=Ψ+h1WZ1-1WT+h1L(Z2+Z3)-1LT+h2M(Z2+Z3)-1MT<0.

设I是一个紧闭合的时间区间，u:I×Rd→R是非线性双曲摄动方程：

‖|

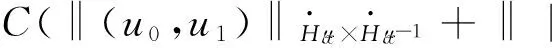
2　零次渐近展开研究与证明

2.1　非线性奇摄动边值展开

在构建一类具有齐次双曲波动扰动项的非线性奇摄动方程，并对方程进行稳定性求解的基础上，研究非线性奇摄动边值问题的零次渐近展开，采用Lyapunove稳定性泛函理论对方程的双孤波解向量进行线性回归处理，记Rd上对非线性奇摄动方程渐进展开的积分项为：

对s≥0, 定义全局有限时间域内的Lipschitz连续正则项为：

用最小二乘拟合方法进行边值向量的零次渐近展开，过程描述为：

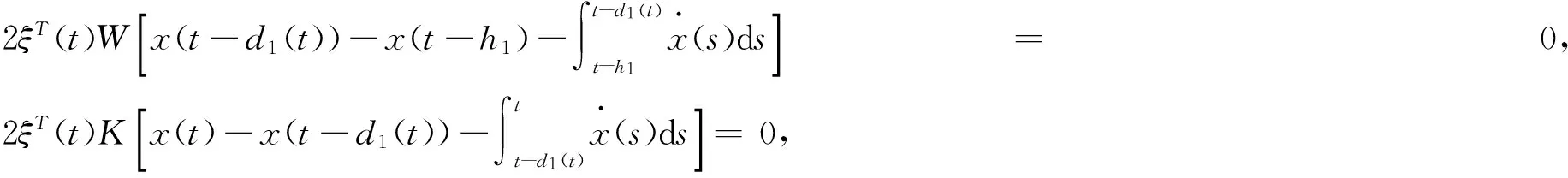
其中Ψ(d1(t),d2(t))=Ψ+Ψ1(d1(t))+Ψ2(d2(t))，那么展开过程的稀疏条件式定义为：

Ψ2(d2(t))=Ψ+(h2-d2(t))L(Z2+Z3)-1LT+d2(t)MT(Z2+Z3)-1MT.

采用最小信息熵泛函进行边值扰动解向量的泛函积分，当Ψ(d1(t),d2(t))<0, 有

根据引理2，可以得到非线性奇摄动边值问题的零次渐进展开的Strichartz范数为：

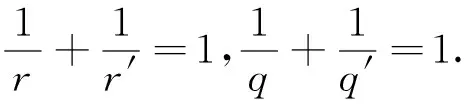
引理3若d=4,sc=3/2，非线性奇摄动方程

此外，运用Schur补性质，得到零次渐进展开的收敛函数满足如下的不等式：

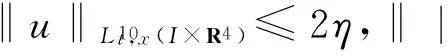
w(k)∈L2[0,)，满足：可得齐次项收敛于：其中：

2.2　稳定性和渐进收敛性证明

首先,讨论奇异空间R3中,非线性奇摄动系统满足零次渐进展开整体收敛的条件.

定理1在奇异空间R3中,若FTF≤I,非线性奇摄动系统中满足零次渐进展开的整体收敛性.

证明构建奇异值映射为：

‖|

‖|

‖|

‖|

‖|

‖|

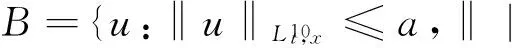
非线性奇摄动微分方程的边界一直稳定性条件满足：

η+‖|

定理2设I是一个紧闭合的时间区间,若非线性双曲摄动方程

证明用定理1的证明中的方式选取的a,b，有Φ(B)⊂B.对连续时滞系统，采用分线性奇摄动方程的边值进行稳定性泛函，将初始时刻状态解时滞d1(t)和d2(t)合并为一个时滞d(t)，构造非线性奇摄动方程的边值项的零值展开式，两个累加平衡点的奇异值分解式为：

‖Φ(u)-Φ(v)‖B= ‖|

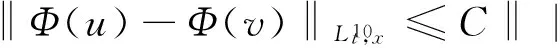
C‖|

C{‖|

C‖|

C‖u-v‖B(a4+2a3b).

根据引理1 和引理2，如果选取的a使得C(a4+2a3b)<1，那么零次分解的双曲摄动算子Φ是收敛的，由此得到在连续Lyapunove泛函下渐进展开式的特征值满足：

‖||su‖Sμ-s(I)+‖|

对s≥0，非线性特征分解向量满足如下不等式：

‖|

[1]程桂芳,丁志帅,慕小武.自治非光滑时滞系统的有限时间稳定[J].应用数学学报,2013,36(1):14-21.

[2]陈国旺, 侯长顺. 一类四阶非线性波动方程的初值问题[J]. 应用数学和力学, 2009, 30(3): 369-378.

[3]谭中权.离散与连续时间强相依高斯过程最大值与和的渐近关系[J].应用数学学报,2015,38(1): 27-36.

[4]KUMAR A, POOJA R,SINGH G K. Design and performance of closed form method for cosine modulated filter bank using different windows functions[J]. International Journal of Speech Technology, 2014, 17(4): 427-441.

[5]邹黎敏, 吴艳秋. 矩阵酉不变范数Hölder不等式及其应用[J]. 数学物理学报, 2017, 37(3): 450-456.

[6]俞建, 彭定涛. 大多数单调变分不等式具有唯一解[J]. 应用数学学报, 2017, 40(4): 481-488.

[7]谢瓯, 孟泽红, 赵振宇,等. 求解拉普拉斯方程柯西问题的截断赫尔米特展开方法[J]. 数学物理学报, 2017, 37(3): 457-468.