刘小刚 ，　欧阳自根,　惠小健

(1.西北大学现代学院 基础部, 陕西 西安 710130；2.西京学院 理学院，陕西 西安 710123；3.南华大学 数理学院, 湖南 衡阳 421000)

分数阶微分方程是微分方程理论的一个新的重要分支，在工程力学、高分子材料解链、牛顿力学等领域有广泛的应用.对于共振情形下分数阶微分方程的边值问题，众多学者作了研究，取得了许多成果[1-6]，但是关于具P-Laplacian算子的高维多时滞的分数阶微分方程的边值问题的研究较少.

本文将研究如下一类具P-Laplacian算子的分数阶时滞微分方程边值问题：

(1)

N-2bi∈R，0<γ<α,f:[0,1]×Rn→R满足Caratheodory条件,Dα,Jα分别是标准的Riemann-Liouville分数阶微分、积分. 对比文献，本文弱化了分数阶微分的边值条件，推广和改进已有工作.

令Y=C[0,1]，范数‖y‖令Z=L1[0,1],范数‖y‖1=|y(t)|dt;

X={u|u,Dα-iu(θi(t))∈Y,i=1,2,…,N-1},其中α>0,N=1+[α].范数记作‖u(t)‖=‖u(t)‖定义算子L:domL∩X→Z，其中

定义算子N:X→Z，Nu(t)=f(t,u(t-τ),Dα-1u(θ1(t))…Dα-(N-1)u(θN-1(t)))，则边值问题(1)等价于算子方程Lu=Nu.

(1)Lx≠λNx，(x,λ)∈[(domLKerL)∩∂Ω]×(0,1)；(2)Nx∉ImL，x∈KerL∩∂Ω；(3) deg{JQN,∂Ω∩KerL,0}≠0,这里J:ImQ→KerL是一个线性同构.

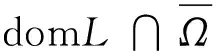
引理2对于算子L有

证明由Lu=0,得到φp(Dαu(t))=Jβy+c0+c1t+…+cN-1tN-1.因为(φp(Dαu(0)))(j)=0,有c0=c2=…=cN-1=0.于是φp(Dαu(t))=Jβy(t).因为(u(0))(i)=0,于是u(t)=Jα(φq(Jβy(t)))+dtα-1.故KerL={dtα-1,d∈R}.ImL的正确性易验证，在此不再赘述.

证明过程类似于[8]中引理3.2.2的证明.

证明由边值条件可知，ImP=KerL，易验证P2=P，则P是幂等算子.显然KerL∩KerP={0}，于是X=KerL⊕KerP，对任意的y∈L1[0,1]，有Q2y=Qy. 则Z=ImL⊕ImQ.而dimKerL=dimImQ=CoKerL=1，则映射L是一个指标为零的Fredholm算子.由算子P,KP的定义易见算子L:ImL→domL∩KerP的逆算子为KP. 事实上，对y∈ImL,LKpy=y(t)，对u∈domL∩KerP,KpLu=Jαφq(φp(Dαu)+citi)，显然ci=0,i=1,…,N-1.于是KpLu=JαDαu(t)=u(t).因此KpLu=u，这表明KP=(L|domL∩KerP)-1.

引理5算子KP(I-Q)N:X→X全连续.

引理5的证明类似文献[8]中引理2.3的证明.记

定理1假设存在函数l(t),li(t)∈L1[0,1],i=0,1,…,N-1，使得

(2)

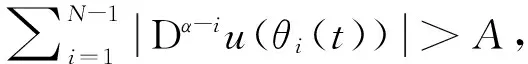
(3)

(H3) 存在常数A*>0,使得对任意的常数e∈R,如果|e|>A*,有I>0或I<0.

则共振边值问题(1)在X中至少存在一解.

‖u‖

(4)

注意到Lu=λNu, 因此φp(Dαu(t))=λJβNu+citα-i.结合边界条件(φp(Dαu(0)))(j)=0,有

φp(Dαu(t))=λJβNu.

(5)

由(2)、(5)有

‖u(t)‖

令Ω2={u∈KerL|Nu∈ImL},对u∈Ω2，有

u∈KerL={u∈domL|u=dtα-1,t∈[0,1],u=0,t∈[-τ,0],d∈R}

则QNu=0，由(H2)得|Dα-1u(t)|≤A,则|Dα-1dtα-1|≤A,即|d|≤A/Γ(α).Ω2有界.

令Ω3={u∈KerL|λJu+(1-λ)QNu=0,λ∈[0,1]}，这里

对任意的u∈Ω3，有λdtα-1=-(1-λ)QNu,进一步有

如果λ=1，则d=0显然成立；否则，如果|d|≤A*，考虑I>0，有-(1-λ)(dQNu)<0，这与λd2>0矛盾.因此Ω3是有界. 如果式I<0成立，则令Ω3={u∈KerL|λJu-(1-λ)QNu=0,λ∈[0,1]}，同理可证Ω3是有界的.

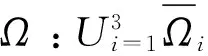
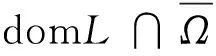
定理2假设定理1中的(H2)、(H3)成立，并且满足

(H6)am0/m1+bn0<1,则边值问题(1)存在唯一解.

证明存在性显然成立，下面证明唯一性.假定u1,u2∈X是边值问题(1)的两个解. 令u=u1-u2，于是

Dβφp(Dαu(t))=f(t,u1(t-τ),Dα-1u1(θ1(t)),…,Dα-(N-1)u1(θN-1(t)))-f(t,u2(t-τ),Dα-1u2(θ1(t)),…,Dα-(N-1)u2(θN-1(t))),注意到ImL=KerL，有

f(s,u2(s-τ),…,Dα-(N-1)u2(θN-1(s)))]}ds,

由函数f的连续性，存在t0∈(0,1)使得

f(t0,u1(t0-τ),…,Dα-(N-1)u1(θN-1(t0)))-f(s,u2(t0-τ),…,Dα-(N-1)u2(θN-1(t0)))=0 .

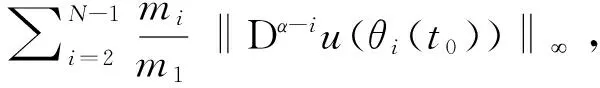
注意到 ‖u‖,‖Dαu‖,‖Dα-iu‖≤‖u‖,于是根据式(6)有,因此‖u‖=0,即u1(t)=u2(t),t∈[0,1].

(刘小刚现在为西京学院理学院讲师)

[1]吕秋燕，刘文斌，唐敏，等.带P-laplacian算子的分数阶微分方程多点边值问题解的存在性[J].湖南师范大学自然科学学报，2016，39(1):80-84.

[2]苏小凤，贾梅，李萌萌.共振条件下分数阶微分方程积分边值问题解的存在性[J].山东大学学报理学版，2016,51(8):66-73.

[3]卢亮，郭秀凤.带P-laplacian算子的分数阶微分方程非局部边值问题解的存在性[J].高校应用数学学报，2015，30(3):262-270.

[4]ZHONG W X,CHU Y D. Existence of solutions for fractional differential equntions with multi-point boundary conditions[J].Commun Nonlinear Sci Numer Simulat，2012,17(1)：1142-1148.

[5]孙倩,刘文斌.一类奇异分数阶微分方程积分边值问题正解的存在性[J].数学的实践与认识,2017,47(17):295-306.

[6]刘小刚，欧阳自根.一类具共振条件的分数阶多点边值问题解的存在性[J].湘潭大学自然科学学报，2017，39(2):121-124.

[7]CHEN F L. Coincidence degree and fractional differential equntions with impulses [J].Computers and Mathematics with Applications，2012,64：3444-3455.

[8]白占兵. 分数阶微分方程边值问题理论及其应用[M].北京：中国科学技术出版社，2012.

[9]葛渭高. 非线性微分方程边值问题[M].北京：科学技术出版社，2009.

[10]郭大钧，孙经先，刘兆理. 非线性常微分方程泛函方法边[M].济南：山东科学技术出版社，1995.