杨水平,　刘红良

(1. 惠州学院 数学与大数据学院,广东 惠州 516007;2.湘潭大学 数学与计算科学学院，湖南 湘潭 411105)

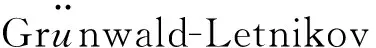
(1)

其中1<α≤2,s>0,f:D=[0,L]×[0,T]×R×R→R是给定连续函数且满足Lipschitz条件

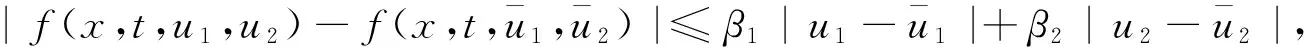
(2)

本节将构造问题(1) 的差分格式. 取时间步长τ=T/N，且使得s=mτ， 其中m为某一个正整数，则tn=nτ,n=0,1,…,N.对于有限区间Ω=[0,L] ，令xi=ih,i=0,1,…,M, 其中h=L/M为空间步长.为了在数值求解(1)的过程中避免求解非线性方程组，问题(1)时间离散时，本文对于线性部分采用隐式方法，对于非线性部分采用显式方法.对于空间分数阶导数采用具有二阶精度的分数阶中心差分格式.首先给出如下的半离散形式：

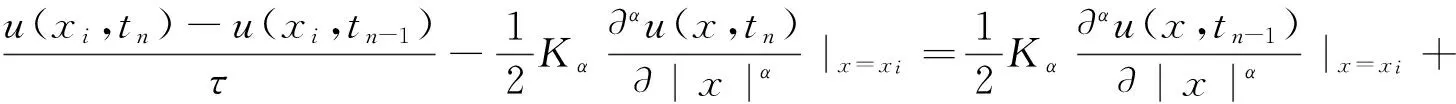
(3)

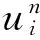
(4)

式中μα=τKαcα/2hα.式(4)还可以简写成为如下形式

(I+D)Un=(I-D)Un-1+τF(Un-1).

(5)

(6)

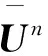
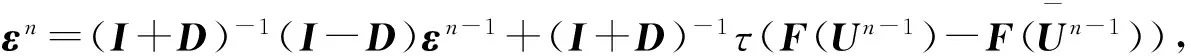
‖(I+D)-1(I-D)‖

可得‖εn‖≤‖(I+D)-1(I-D)‖‖εn-1‖+τ‖(I+D)-1‖(β1‖εn-1‖

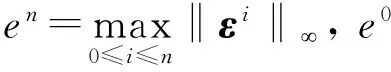
en≤‖(I+D)-1(I-D)‖en-1+τ‖(I+D)-1‖(β1+β2)en-1≤(1+τC)en-1,

其中C=β1+β2, 则由上式可知en≤(1+τC)ne0≤exp(TC)e0.

证明假设Un和un分别为方法(5)的数值解和真解，un=[u(x1,tn),u(x2,tn),…,u(xM-1,tn)]T, 以及εn=Un-un. 由[11]可知(I+D)εn=(I-D)εn-1+τ(F(Un-1)-F(un-1))+O(τ2+τh2),利用Lipschitz条件 (2), 则有

‖(I+D)-1(I-D)‖

进一步可得

‖εn‖≤‖(I+D)-1(I-D)‖‖εn-1‖+τ‖(I+D)-1‖(β1‖εn-1‖+β2‖εn-m-1‖)+O(τ2+τh2).

en≤‖(I+D)-1(I-D)‖en-1+τ‖(I+D)-1‖(β1+β2)en-1+O(τ2+τh2)≤(1+τC)en-1+O(τ2+τh2),

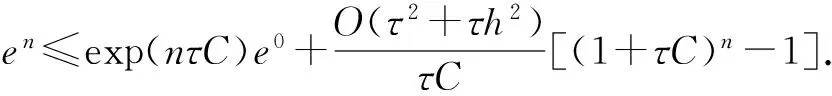
en≤O(τ2+τh2)/τC[(1+τC)n-1]≤O(τ+h2)[exp(TC)-1]/C≤C*(τ+h2)=O(τ+h2),

其中C*=(exp(TC)-1)/C.

(7)

例1考虑如下分数阶时滞扩散微分方程初值问题

(8)

式中：T=2,s=0.5,Kα=1, 1<α≤2,

f(x,t,u(x,t),u(x,t-s))=u(x,t)u(x,t-s)-x2(1-x)2e-t-x4(1-x)4e-2t+τ+[e-t/2cos(απ/2)].

该问题的真解u(x,t)=x2(1-x)2e-t.

很容易验证u(x,t)∈C(2,2)([0,L],[-s,T]), 且f满足条件 (2). 利用方法 (5) 求解问题 (8)，当取α=1.5， 在不同网格剖分时数值解与真解的最大误差及相应的误差阶如表1所示. 当分别取α=1.5 和α=1.8，利用方法 (5) 的外推格式求解， 在不同网格剖分时数值解与真解的最大误差及相应的误差阶如表2所示. 从表 1 可知方法 (5) 的空间离散的收敛阶达到二阶，时间离散的收敛阶仅有一阶.利用外推技巧改进后的时间和空间离散的收敛阶基本达到了 2 阶，验证了本文的理论结果， 说明方法 (5) 和利用外推技巧获得的数值格式 (7) 求解问题(8)是比较高效的.

表1　方法 (5) 求解问题 (8) 的误差及其误差阶

表2　方法 (5) 的外推格式求解问题 (22) 的误差及其误差阶

[1]PODLUBNY I.Fractional differential equations[M].SANDIEGO:Academic Press, 1999.

[2]DIETHELM K, WALZ G.Numerical solution of fractional order differential equations by extrapolation[J]. Numerical Algorithms, 1997,16(3-4):231-253.

[3]DIETHELM K,FORD N J, FREED ALAN D.A predictor-corrector approach for the numerical solution of fractional differential equations[J]. Nonlinear Dynamics, 2002,29:3-22.

[4]PEDAS A,TAMME E.On the convergence of spline collocation methods for solving fractional differential equations[J]. J Comput Appl Math, 2011,235: 3502-3514.

[5]LI C P, CHEN A, YE J J.Numerical approaches to fractional calculus and fractional ordinary differential equation[J]. Journal of Computational Physics, 2011,230:3352-3368.

[6]孙志忠，高广花. 分数阶微分方程的有限差分方法 [M]. 北京:科学出版社, 2015.

[7]LI X J, XU C J. A space-time spectral method for the time fractional diffusion equation[J]. SIAM Journal on Numerical Analysis, 2009,47:2018-2131.

[8]SONG F Y, XU C J.Spectral direction splitting methods for two-dimensional space fractional diffusion equations[J]. Journal of Computational Physics, 2015,299:196-214.

[9]ZHUANG P, LIU F, TURNER I, et al. Galerkin finite element method and error analysis for the fractional cable equation[J]. Numerical Algorithms, 2015,72(2):447-466.

[10]BU W P, TANG Y F,YANG J Y. Galerkin finite method for two-dimensional Riesz space fractional diffusion equations[J]. Journal of Computational Physics, 2014,276: 26-38.

[11]刘发旺， 庄平辉， 刘青霞. 分数阶偏微分方程数值方法及其应用 [M]. 北京:科学出版社, 2015.

[13]CAO W, ZENG F, ZHANG Z, et al. Implicit-explicit difference schemes for nonlinear fractional differential equations with non-smooth solutions[J].Siam Journal on Scientific Computing, 2016, 38(5):A3070-A3093.

[14]陈珊珊. 几类时滞反应扩散方程的动力学性质分析 [D]. 哈尔滨:哈尔滨工业大学, 2012.

[15]HAO Z, FAN K, CAO W, et al. A finite difference scheme for semilinear space-fractional diffusion equations with time delay[J]. Applied Mathematics and Computation, 2016, 275:238-254.

[16]RAN M H, HE Y. Linearized Crank-Nicolson method for solving the nonlinear fractional diffusion equation with multi-delay[J/OL]. International Journal of Computer Mathematics, 2017. https://doi.org/10.1080/00207160.2017.1398326.