杨海波

武汉理工大学政治与行政学院yanghaibo112@qq.com

1 《算术的基本规律》中的逻辑理论FL

弗雷格《算术的基本规律》中的逻辑理论本质上是如下带有完整二阶存在概括规则的二阶逻辑加上函数外延存在公理、函数相等公理、函数外延相等公理等三条非逻辑公理（即著名的弗雷格的公理V）的二阶理论FL：

FL语言的初始符号：

1.指示个体的变元：x,y,z,x1,y1,z1,...；

2.指示性质或关系（仿照弗雷格，我们也把性质与关系称为以真假为函数值的函数）的变元：P,F,R,P1,F1,R1,...（对每个n，都有无穷多个n元函数变元。其实为证明休谟原则进而发展算术弗雷格只需要一元概念与二元关系变元）；

3.外延算子：†；

4.通常的真值联结词、量词与等词；

FL的项与公式的定义：

1.个体变元是项；

2.如果t1,t2是项，则t1=t2是公式；

3.如果F与Q是函数符号，则F=Q是公式；

4.如果F是n元（性质与关系）函数符号，t1,t2,...,tn是项，则F(t1,t2,...,tn)是公式；

5.设F是（性质与关系）函数符号，则†F是项；

6.如果φ,ψ是公式，则(φ∧ψ),(φ∨ψ),(φ→ψ),(φ↔ψ),¬φ都是公式；

7.设x是个体变元，φ是任意公式，则∀xφ是公式（∃xφ是¬∀xφ的缩写）；

8.设F是函数变元，φ是任意公式，则∀Fφ是公式（∃Fφ是¬∀F¬φ的缩写）；

9.除此之外没有其它的项与公式。

FL的公理系统：

FL的公理系统为常见的带等词的一阶公理化逻辑系统加上如下公理与规则：

1.二阶全称例示公理：∀Fφ(F)→φ(P)，其中P对φ中的F是代入自由的。（其中，P与F是函数变元符号，由这条公理，我们可以得到简单的二阶存在引入规则，即如果φ(P)是定理，则∃Fφ(F)也是定理，其中P对φ中的F是代入自由的。这条公理对应于弗雷格明确给出的二阶全称例示公理。）

2.完整的二阶存在概括公理：如果F不在φ(x1,x2,...,xn,y1,y2,...,ym)(m≥0,n≥1)中自由出现，则

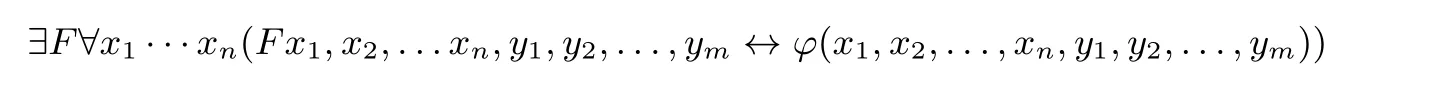
是系统的定理。（弗雷格用带二阶量词的公式代换函数变元，这实质等价于肯定了完整的二阶存在概括规则。参见[8]，第40–43页。）

3.函数或概念相等的公理组：∀P∀F(P=F↔∀x(Px↔Fx))（二元函数的公理为：∀P∀F(P=F↔∀x∀y(Pxy↔Fxy))，多元函数变元的情况相似。二阶逻辑中，等号与规范等号的公理不必是初始的，也可以通过定义引进来。）

4.函数外延存在公理：∀P∃x(x=†P)。（弗雷格在语言中引进了一个外延算子，这个算子作用于任何一个函数后得到这个函数的域值（或图）。这相当于在语义中假设了每个函数都有一个外延。我们用这条公理把这个假设明确地说出来。）

5.函数外延相等公理：∀P∀F((†P= †F)↔ ∀x(Px↔ Fx))（二元函数的公理为：∀P∀F(†P= †F)↔ ∀x∀y(Pxy↔ Fxy))，多元函数变元的情况相似）。（这条公理即弗雷格的公理V。）

6.二阶全称概括公理：如果φ(F)是定理，则∀Fφ(F)也是定理。

根据二阶存在概括公理，如果F不在φ(x1,x2,...,xn,y1,y2,...,ym)中自由出现，则∃F∀x1···xn(F(x1···xn,y1,y2,...,ym)↔ φ(x1,x2,...xn,y1,y2,...,ym)是系统定理。再根据函数相等公理，可知

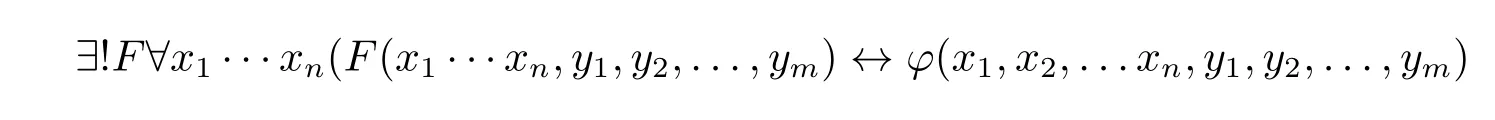
是系统定理。进而我们可以扩张语言，相应于每一个形如φ(x1,x2,...,xn,y1,y2,...,ym)的公式，我们引入一函数符号，不妨记为λ(z1,z2,...,zn)φ(z1,z2,...,zn,y1,y2,...,ym)，用

作为新引进的函数的定义公理。当然同一公式可能有不同函数与其对应，但根据函数相等公理，我们能够证明对应于同一公式的不同函数相等。由于

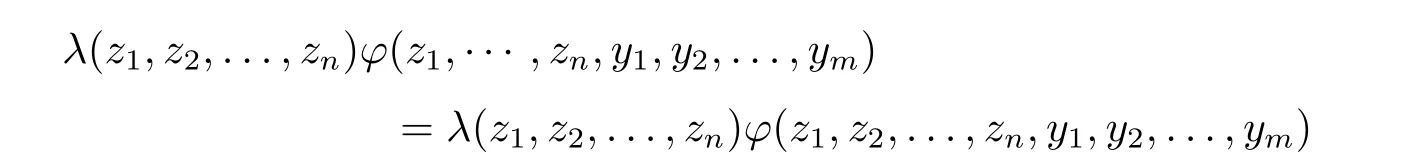
由新函数的定义公理与全称例示公理有如下λ-变换规则：

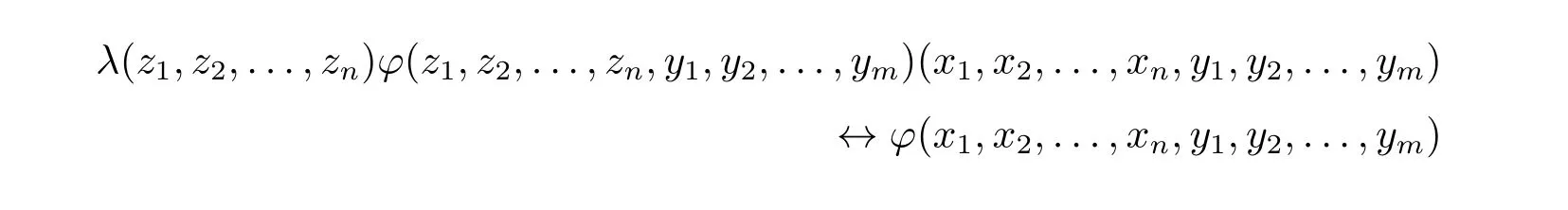
而对于这个扩张后的语言的每个形如λ(z1,z2,...,zn)φ(z1,z2,...,zn,y1,y2,...,ym)的函数，相应的扩展形成规则5，我们可以得到相应的个体†λ(z1,z2,...,zn)φ(z1,···,zn,y1,y2,...,ym)。

从语法上讲，上述逻辑理论FL会产生罗素悖论。

考虑公式∃F(y=†F∧Fx)，由上面的讨论可知有概念λ(x,y)(∃F(y=†F∧Fx))符合相应的定义公理，不妨记此概念为x∈y；仿照弗雷格，我们先来论证Fx↔x∈†F是系统的定理，其中F是函数变元符号。（[3]，附录I，第123页）假设Fx，由于†F= †F，进而有†F= †F∧Fx，由简单的存在引入规则，可有∃P(†F= †P∧Px)，即x∈†F。再假设x∈†F，按属于定义有概念P使得†F=†P且Px，再由外延相等公理可得Fx。由于上述论证中只使用了简单的逻辑规则，故上述论证可在FL中形式化，从而Fx↔x∈†F是系统的定理。接下来，我们考虑罗素悖论如何推出。

由于可以推演出罗素悖论，弗雷格曾在《算术的基本规律》第二卷的附录II中对公理V做了一定的限制，但后人证明，弗雷格的修改是不成功的。（[7]，第76–77页）

2 在FL中发展算术

下面我们概要地考察弗雷格如何在FL中发展算术。弗雷格要做的是在FL中定义算术的基本概念以及推出算术的基本定理。为此弗雷格首先给出了概念间等数、概念的数的定义，然后给出了休谟原理的证明。

设F,G是一元函数，定义F ≈ G=df∃R(∀x∃!yRxy∧∀x∃!yRyx∧∀x(Fx→∃y(Gy∧Rxy)∧∀x(Gx→∃y(Fy∧Ryx))。在带完整二阶存在概括规则的二阶逻辑下，容易给出函数之间的≈关系是等价关系的语法证明。在《算术基础》（[4]，第85页）中，弗雷格把一个函数的数定义为此函数的≈等价类。换言之，若用#F表示概念或函数F的数，则#F={G|F≈G}。由于在《算术的基本定律》中明确地给出外延存在公理，以及外延相等公理，使得弗雷格可以把函数用其外延来替代，进而把函数的数定义为与其≈等价的函数的外延的类。用#F表示概念F的数，弗雷格给出的显定义为：#F=df†λy∃P(y=†P∧F≈P)。换言之，概念F的数是一阶概念λy∃P(y=†P∧F≈P)的外延，而一个对象落入一阶概念λy∃P(y=†P∧F≈P)当且仅当它是某个与概念F等势的概念的外延。

根据概念的数的显定义与函数的外延相等公理可以得到所谓的休谟原则：#F=#G↔F≈G。

假设#F=#G，由#的定义有†λy∃P(y= †P∧F ≈ P)= †λy∃P(y= †P∧G ≈P)，根据函数外延相等公理知道 ∀x(λy∃P(y= †P ∧F ≈ P)x ↔ λy∃P(y=†P∧G ≈ P)x)。由变换定理有 ∀y(∃P(y= †P ∧F ≈ P)↔ ∃P(y= †P ∧G ≈ P))，而†F=†F且F ≈F，从而有∃P(†F=†P∧G≈P)，不妨以P做存在例示，据外延相等公理，由†F=†P得到∀x(Px↔Fx)，从而可用F置换G≈P中的P，得到F≈G。

假设F ≈ G且并非#F=#G，由#的定义有 †λy∃P(y= †P ∧F ≈ P)̸=†λy∃P(y= †P ∧G≈P)，进而由函数外延相等公理有 ∃x((λy∃P(y=†P ∧F ≈P)x∧ ¬λy∃P(y= †P ∧ G ≈ P)x)∨ (¬λy∃P(y= †P ∧ F ≈ P)x∧ λy∃P(y=†P∧G ≈ P)x))。不妨只考虑∃x(λy∃P(y= †P∧F ≈ P)x∧¬λy∃P(y= †P∧G ≈P)x))情况，用z来做存在的例示，据变换定理有∃P(z=†P∧F≈P)∧¬∃P(z=†P∧G≈P))，不妨设z=†Q∧F≈Q，再由假设F≈G，可得z=†Q∧Q≈G，矛盾于¬∃P(z=†P∧G≈P))，进而#F=#G。

在用函数外延相等公理与概念的数的显定义证明休谟原则后，弗雷格进一步地定义了广义的数、0、后继与自然数的形式定义，并推理出了常见的戴德金皮亚诺公理。但不幸的是，上述FL是不一致的。

回顾系统FL，它只是在带完整二阶存在概括规则的基础上加上了外延存在公理与函数外延相等公理（即上述FL的公理4与5）。若抛弃外延存在公理与函数外延相等公理，进而抛弃利用函数的外延来定义的概念的数的显定义，而加入休谟原则作为公理，这就足以推理出戴德金皮亚诺公理，并且只加入休谟原则作为非逻辑公理的的二阶理论是一致的。在1983年，Wright注意到仅利用休谟原则与二阶逻辑好像不足以推出罗素悖论，并指出，用休谟原则就足以推出二阶Peano算术，即休谟原则加上二阶逻辑蕴涵皮亚诺公理。（[5]）Boolos也称此为弗雷格定理。人们把休谟原则加上二阶逻辑这个理论称为弗雷格算术（FA）。Wright同时也猜测弗雷格算术是一致的。（[5]，第154–158页）Boolos在1987年《弗雷格算术基础的一致性》一文中肯定了Wright的猜想，给出了一致性的证明。（[1]）在国内，徐明明先生曾较早地概要性地介绍过这一具有重要意义的成果。（[6]）

3 弗雷格算术FA是一致的

FA的语言与公理系统：

1.去掉上述FL中的外延符号†，进而去掉项的形成规则5：设F是函数符号，则†F是项。只保留一元概念变元与二元关系变元，去掉三元以及以上的函数变元。

2.加入一元性质常量符号：#；加入项的形成规则：如F是一元性质（或概念）符号，#F（直观代表概念F的数）是项。

3.加入原子公式形成规则：#F=#G是原子公式。

4.去掉FL中的公理4与5，加入休谟原则作为唯一非逻辑公理：#F=#G↔

F≈G。其中，“G≈F”意为概念G与F等势，有通常的二阶定义式：∃R(∀x(Fx → ∃!y(Gy∧Rxy))∧ ∀y(Gy → ∃!x(Fx∧Rxy)))。

定理1 FA是一致的。

证明:令结构M= 〈U,℘(U×U),P(U),s〉，其中，U={0,1,2,...,ℵ0}，ℵ0是最小的无穷基数，(U)是指U的幂集；s是(U)到U的函数，且对每个U的子集V或V ∈(U)，s(V)=|V|，其中|V|是指V 的基数；由于ℵ0∈ U，函数s是全函数，令函数s为FA中唯一非逻辑函数常量符号♯的解释。结构M上的任意变元指派σ对每个一元概念变元F，σ(F)∈ ℘(U)；且对每个二元关系变元R，σ(R)∈ ℘(U×U)；对每个概念变元F，σ(#F)=s(σ(F))=|σ(F)|∈U。从而对每一元概念变元F与G：σ(#F=#G)为真当且仅当s(σ(F))=s(σ(G))当且仅当|σ(F)|=|σ(G)|当且仅当σ(F ≈ G)为真，即公式：∃R(∀x(Fx → ∃!y(Gy∧Rxy))∧∀y(Gy → ∃!x(Fx∧Rxy)))在变元指派σ下的值为真，简言之，σ(#F=#G)为真当且仅当σ(F≈G)为真，从而休谟原则在结构M上的任意指派下都为真，进而休谟原则在M中为真，即休谟原则与二阶逻辑是一致的。 □

4 戴德金皮亚诺公理的证明

二阶的戴德金皮亚诺公理系统包含如下5条非逻辑公理：

1.0是自然数，符号表示为：Num(0)；

2.每个自然数都有唯一的后继且是自然数，符号表示为：∀x(Num(x)→ ∃!y(Num(y)∧ Sxy))；

3.0不是任何自然数的后继，符号表示为：∀x(Num(x)→¬Sx0)；

4.后继函数是单射，符号表示为：∀x∀y∀z(Num(x)∧Num(y)∧Num(z)∧Sxy∧Szy → x=z))；

5.数学归纳法原则，即：∀F((∀x∀y(F(x)∧Sxy → F(y))∧F(0))→ ∀x(Num(x)→F(x)))。

算术基本概念的定义：

再考虑公式∃P(x=#P)，根据上述对完整二阶存在概括公理与函数相等公理的讨论，有函数常量λx∃P(x=#P)满足相应的定义公理。为方便，我们把此函数常量简记为N，Nx意在表示x是一个数。类似地，我们可以引进如下函数或关系常量：

·Nx↔λx∃P(x=#P)x（x是广义的数，包括无穷数）；（[4]，第72节）

·0：#λx(x ̸=x)（0 的定义）；（[4]，第 74 节）

·Sxy↔ λ(x,y)∃P∃u(y=#P ∧Pu∧x=#λv(Pv∧v̸=u))xy（y是x后继关系）；（[4]，第 76节）

·S⋆xy ↔ λ(x,y)∀P((∀u∀v(Pu∧Suv → Pv)∧ ∀u(Sxu → Pu)→ Py))xy（x＜y或x是y的真祖先）；（[2]，第60页）

·Num(x)↔λx(S⋆0x∨x=0)x（x是自然数或有穷数）。（[4]，第83节）

在祖先关系定义中，∀u∀v(Pu∧Suv→Pv)是说P相对于S是一个遗传性质。这个定义是说：S⋆ab当且仅当对任何的遗传性质，如果x的每一后继具有它，那么y就具有。关系S⋆是后继关系S的传递闭包，当S⋆ab成立时，我们也说a是b的R真祖先。直观上，S⋆ab成立当且仅当有一条经过a且只通过有穷多点的到达b的通路。由于我们定义了什么是数（即上述定义中的Nx，可以包括自然数与无穷数），定义了0与单值性的后继关系S，那么定义x是一个自然数当且仅当S⋆0x或x=0，也就是直观上从0开始走有穷步可到达x，进而排除了无穷数。这样，什么是自然数或有穷数（上述定义中的Num(x)）就定义出来了。利用休谟原则、λ-变换规则与上述几个定义，可以推出戴德金皮亚诺系统的五条公理，这也即所谓的弗雷格定理。我们下面概要地勾勒出这几个公理在FA中的证明。

定理2 戴德金皮亚诺公理5是系统FA的定理。

证明:上述的自然数的定义就足以保证数学归纳法原则是成立的。假设性质P是遗传的，即满足：∀x∀y(P(x)∧Sxy→P(y))，且0具有性质P，我们来证明∀x(Num(x)→F(x))。若x=0，由假设知0具有P，若S⋆0x，由P相对于关系S是遗传的，且由于0有性质P，进而0的后继都有P，根据S⋆0x的定义知道所有的自然数都有性质P，从而数学归纳法则成立。 □

定理3 戴德金皮亚诺公理3是系统FA的定理。

证明概要：利用“0”的定义、休谟原则与“≈”的定义即可直接证明引理1：#F=0↔ ∀x¬Fx是成立的。（[4]，第75节）这条引理是在说概念F的数为0当且仅当没有个体落在其下。在这条定理的基础上，我们容易看出¬Sx0成立，进而得到上述的戴德金皮亚诺公理3，即0不是任何自然数的后继，符号表示为：∀x(Num(x)→ ¬Sx0)。

定理4 戴德金皮亚诺公理4是系统FA的定理。

证明概要：利用后继关系“S”的定义、休谟原则、“≈”的定义与λ-变换规则即可直接证明引理2：Smn∧Sm′n′→ (m=m′↔ n=n′)是成立的。（[4]，第78节）这条定理是在说直接后继关系S是一一对应的。这样，我们就可以直接得到上述的戴德金皮亚诺公理4，即后继函数S是单射，用先前的符号可以表示为：∀x∀y∀z(Num(x)∧Num(y)∧Num(z)∧Sxy∧Szy → x=z))。

定理5 戴德金皮亚诺公理1是系统FA的定理。

证明:根据自然数Num(x)的定义即：S⋆0x∨x=0，因0=0，所以0是自然数，即上述的戴德金皮亚诺公理1成立。 □

这样，我们并不太费力地就得到了皮亚诺四条公理。麻烦的是后继存在公理：∀x(Num(x)→ ∃!y(Num(y)∧Sxy))。我们在上面提到，我们可以证明：Smn∧Sm′n′→(m=m′↔n=n′)，进而唯一性容易得到。下面我们勾勒出后继存在性的证明。

我们不妨定义x≤y↔dfS⋆xy∨x=y。

引理3: Sxy→S⋆xy（直接后继关系蕴含真祖先关系）。（[2]，第66页）

引理4: S⋆xy∧S⋆yz→S⋆xz（真祖先关系是传递的）。（[2]，第69页）1引理3、4的证明略。

引理5: S⋆xn→(∃ySyn∧∀m(Smn→(S⋆xm∨x=m)))

（若x＜n，则n一定有前驱m，且x＜m或x=m）。

证明:假设S⋆xn，由S⋆的定义知∀F(∀x∀y(Fx∧Sxy→Fy)∧∀z(Sxz→Fz)→ Fn)成立。令F= λz（∃ySyz∧∀m(Smz → (S⋆xm∨x=m))）。在S⋆xn的假设下，容易验证上述F是遗传的，即若Fv∧Svy，则Fy，即∃mSmy∧∀m(Smy→(S⋆xm∨x=m))。下面证明x的直接后继具有性质F；假设Sxz，由存在引入规则知∃mSmz。假设Smz，由引理2知m=x，继而S⋆xm∨x=m成立。从而∃mSmy∧∀m(Smy→(S⋆xm∨x=m))，即Fz成立。由S⋆的定义、F是遗传的与x的后继具有性质F，我们知道Fn成立，即(∃ySyn∧∀m(Smn→(S⋆xm∨x=m)))成立。 □

引理6: S⋆0n→¬S⋆nn（任何自然数都不是自己的直接后继）。（[4]，第83节）

证明:仿照上一引理的证明，假设S⋆0n，我们令F=λm(¬S⋆mm），然后验证F是遗传的（利用引理3、4与5），并且0的后继具有性质F（利用引理1、3、4与5），进而我们得到n具有性质F，即¬S⋆nn。 □

引理7: Smn∧S⋆0n→ ∀x(x≤m↔x≤n∧xn)。

证明:利用引理3、4、5与6即可直接证明。 □

引理8: Smn∧S⋆0n → S#λx(x≤ m)#λx(x≤ n)。

证明:假设Smn∧S⋆0n，由引理7知道，∀x(x≤ m ↔ x≤ n∧xn)成立，进而可以证明λx(x≤ m)≈ λx(x≤ n∧xn)，根据休谟原则，知道#λx(x ≤ m)=#λx(x ≤ n ∧xn)。令 F= λx(x ≤ n)，知道 #F=#λx(x ≤n)，由λ-变换规则可知Fn成立，并且由#λx(x≤ m)=#λx(x≤ n∧xn)成立知道 #λx(x ≤ m)=#λx(Fx∧xn)成立，进而 ∃F∃y(Fy∧#λx(x ≤n)=#F∧#λx(x≤m)=#λx(Fx∧xy))成立，从而根据后继S的定义知道S#λx(x ≤ m)#λx(x ≤ n)成立。 □

引理9: Syz→ (0≤ y∧Sy#λx(x≤ y)→ (0≤ z∧Sz#λx(x≤ z)))。（[4]，第82节）

证明:利用引理3、4与8即可直接证明。 □

引理 10: S0#λx(x ≤ 0)。（[4]，第 82 节）

证明:利用引理1、5、上述皮亚诺公理3与S的定义直接可以证明。 □

引理11: 0≤n→(0≤n∧Sn#λx(x≤n))。

证明:假设0≤n，由“≤”的定义知S⋆0n∨0=n。

·若0=n，由引理10知S0#λx(x≤0)，继而显然有(0≤n∧Sn#λx(x≤n))

·若S⋆0n，根据S⋆的定义有∀F(∀x∀y(Fx∧Sxy→ Fy)∧∀x(S0x→ Fx)→Fn)。

令F=λn(0≤n→(0≤n∧Sn#λx(x≤n)))。设S0z，显然有0≤0，根据引理10有S0#λx(x≤0)，根据引理9有S0z→(0≤0∧S0#λx(x≤0)→(0≤z∧Sz#λx(x≤ z)))，继而有0≤ z∧Sz#λx(x≤ z)，进而可得Fz。这就证明了0的后继都具有F性质，即∀x(S0x→Fx)。假设Fm与Smy根据F的定义与引理9可得Fy，即F是遗传的。根据S⋆的定义、F是遗传的以及0的后继都具有F性质，可知Fn，即(0≤n∧Sn#λx(x≤n))。这样，0≤n→(0≤n∧Sn#λx(x≤ n))是系统FA的定理。 □

定理6 戴德金皮亚诺公理2：∀x(Num(x)→∃!y(Num(y)∧Sxy))是系统FA的定理。

证明:根据与Num(n)的定义，可知0≤n当且仅当Num(n)，所以引理11就证明了后继的存在性，即Sn#λx(x≤n)，而后继的唯一性由引理2得以保证，这样我们就证明了上述的戴德金皮亚诺公理2。 □

这样，我们就证明了戴德金皮亚诺的五条公理都是弗雷格算术FA的定理。后继存在定理与后继关系是一一的就保证了理论FA承诺了无穷多数的存在。直观上，弗雷格首先定义了0。考虑“x≤0”这个公式，根据二阶存在概括规则，对应于这个公式存在概念λx(x≤0)。可以证明这个概念的数是0的后继。不妨把这个数称为1，那么对应于“x=0∨x=1”这个公式，根据二阶存在概括规则，对应于这个公式存在概念λx(x=0∨x=1)。可以证明这个概念的数是1的后继。以此类推。一般地，利用弗雷格的自然数的定义，我们实质上用数学归纳法证明了，如果y是一个自然数，即Num(y)，那么概念λx(S⋆xy∨x=y)的数就是y的后继。这样弗雷格的理论蕴含着存在无穷多（概念的）数。

5 小结

回顾上述两个逻辑理论FL与FA，FA抛弃了FL的函数外延相等公理、函数外延存在公理，而是把FL的定理休谟原则当做唯一的非逻辑公理，进而FA是FL的子理论。FA是一致的，并且足以解释戴德金皮亚诺公理系统。FL是不一致，可以推演出罗素悖论。从语义上讲，由于二阶逻辑在只有一个个体的模型下也可以是可靠的，标准算术理论要求存在无穷个体对象存在，进而单独的只带完整二阶存在概括规则的二阶逻辑太弱，并不能发展出算术。在二阶逻辑的标准语义学下，二阶量词的取值范围是一阶个体域的幂集，每个一元谓词都被赋值一个个体域的子集。外延存在公理是说每个函数或概念都有一个外延；函数相等公理与外延相等公理放在一起是说函数（或概念）与函数的外延是一一对应的，即不相等的函数有不同的外延，不同的外延对应于不同的函数；再考虑到FL语言形成规则5：设F是函数符号，则†F是项，这条规则是在说函数外延是个体对象。因此，把这四条原则放在一起并要同时为真的话，一定要求存在一个从个体域的幂集到个体域的单射，而这矛盾于康托定理，进而FL是不可满足的。

通过仔细考察弗雷格的逻辑系统以及算术还原为逻辑的推理过程，可以看出弗雷格在用公理五与概念的数的显定义推演出休谟原则后，就不再实质依赖于公理五与概念的数的显定义，只需要休谟原则就足以推演出戴德金皮亚诺的五条公理，休谟原则与带完整二阶存在概括规则的二阶逻辑是一致的，这实质上给出了不同于皮亚诺公理系统的另外一种算术公理化系统。FA一致的且能够解释皮亚诺算术，这是一个有趣且重要的结果。数学家们对算术的研究可谓最为集中，他们给出了所谓戴德金——皮亚诺公理这个对自然数序列的范畴性的刻画。而在弗雷格那里，我们有着自然数的不同的公理化FA。他的刻画只依赖于所谓的休谟原则，而并不需要戴德金——皮亚诺的五条特殊的数学公理。戴德金——皮亚诺公理的得出依赖于我们对自然数序列的直观分析，分析出五条公理。而弗雷格的公理化则完全不同，一些新弗雷格主义哲学家认为这在解释我们关于自然数知识的本性时候，特别是在解释休谟原则何以为真时，我们或许不需要康德的时空直观，而只依赖于“概念的数”概念的分析，从而休谟原则是分析性真理。但从另一个方面讲，弗雷格的公理五蕴含概念的外延存在；休谟原则蕴含概念的数的存在；完整的二阶存在概括公理蕴含概念或关系的存在；而休谟原则加上完整二阶存在概括公理蕴含无穷多的个体对象（数）的存在。这些弗雷格所主张的原理都有存在意涵。一般认为，有存在意涵的原理是不能够仅仅根据语词意义就为真的分析性真理，所以新弗雷格主义哲学家们对此问题仍需给出一个合理的说明或解释。

[1]G.Boolos,1987,“The Consistency of Frege’s Foundations of Arithmetic”,reprinted in G.Boolos(1998),in J.Burgess and R.Jeffrey(eds.),Logic,Logic,and Logic,pp.183–201,Cambridge,MA:Harvard University Press.

[2]G.Frege,1879,“Begriffsschrift,a formula language,modeled upon that of arithmetic,for pure thought”,Reprinted in J.Van Heijenoort(eds.)(1967),From Frege to Gödel:A Source Book in Mathematical Logic,1879–1931,pp.1–82,Cambridge,MA:Harvard University Press.

[3]G.Frege,1964,The Basic Laws of Arithmetic:Exposition of the System,Berkeley,Los Angeles:University of California Press.Translated,and edited with an introduction by Montgomery Furth.

[4]G.Frege,1953,The Foundations of Arithmetic,New York:Harper&Brothers Publishers,J.L.Austin(Trans.).Second revised edition.

[5]C.Wright,1983,Frege’s Conception of Numbers as Objects,Aberdeen:Aberdeen University Press.

[6]徐明明，“弗雷格定理的再发现、证明及其哲学意义”，自然辩证法通讯，2000年第2期，第 23–29页。

[7]杨海波，“弗雷格的逻辑主义之路”，武汉大学学报（人文科学版），2011年第3期，第69–77页。

[8]杨海波，“弗雷格《概念文字》理解的两点注记”，逻辑学研究，2012年第4期，第39–48页。