王新军，朱永忠，李佳蓓

（河海大学 理学院，南京 211100）

0 引言

考虑普通最小二乘回归问题：

其中y为解释变量，y∈Rn，X为回归矩阵，X∈Rn×p，其中p为预测变量数，n为样本观测数，‖⋅‖2是Rn中的欧几里得空间并且β∈Θ⊂Rn。为了更好地提出问题，假设p＜n，XTX非奇异，对于上述问题，普通最小二乘估计（OLS）是最常见的解决方法。然而，在高维问题中，普通最小二乘估计很难处理，一些微小的变化可能导致估计不稳定。比如，观测数据的微小变化就可能导致参数估计的极端变化。

1996年，Tibshirani提出了Lasso估计[1]，其本质是通过L1惩罚对模型系数进行压缩，将没有影响或影响较小的自变量的回归系数自动压缩到零，从而不仅在一定程度上能消除多重共线性的影响，而且在对参数进行估计的同时也实现了对变量的选择。

对于如下有约束的最优化问题：

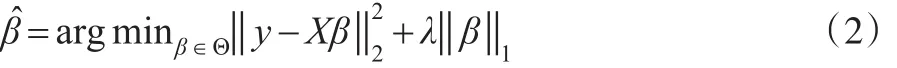
Lasso估计以方差小幅度的降低来换取偏差的少量增加，从而使得均方误差整体上降低。Lasso估计不仅避免了普通最小二乘估计在高维问题中的不稳定性，而且能够达到变量选择的目的。然而Lasso引进的L1惩罚函数不可微[2]，从而导致估计的协方差阵不存在紧集，对于此问题，需要采用重采样方法解决。

2008年，Park T和Casella G提出了Bayesian Lasso方法(BLasso)[3]，在贝叶斯理论框架下，对回归系数引进如下的独立Laplace条件先验：

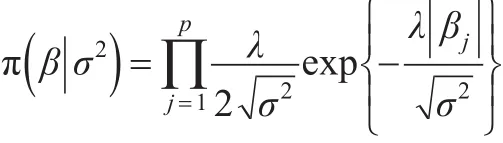
发现其边际后验众数与Lasso给出的估计一致，弥补了Lasso的不足。上述σ2的分布如果不合适会导致最优化求解有多个满足条件的估计值，而不是唯一的，因此σ2的后验分布必须是单峰的。BLasso法避免了采用重抽样方法对协方差阵估计，然而，其未解决正态误差项在极大似然假设下的稳健性。

在很多情况下（基因组学、计量经济学、金融数据等）经常会遇到数据中存在异常值或者当数据不是服从正态分布假设，而是服从重尾分布。在这些情况下，回归系数的估计很有可能受到影响，使得模型预测精度受到影响。

为此，本文改进BLasso方法，在BLasso的基础之上引入两组潜变量，这样做的优势在于：一是允许模型存在误差或者异常值，能够模拟出常见的偏态和重尾分布，从而能够确保模型的稳健性，二是保持模型的共轭性，能够更好地应用Gibbs抽样。在引进潜变量之后，利用边缘极大似然估计方法，对潜变量边际优化，从而得出未知参数的极大似然函数。本文选用层次模型的误差项是逆伽马正态混合分布的尺度参数，这与BLasso层次模型采用的服从t分布的误差项相类似[4]，但是选用了不同的层次模型以及惩罚函数结构，从而能够在已知参数的似然Laplace先验分布的情况下实现更加稳健的Gibbs抽样。通过数据仿真发现，当数据中出现异常值，或者数据服从重尾分布的情况下能够给出相比Lasso，BLasso更加精确的估计以及较好的变量选择。

1 模型及方法

1.1 分层模型

为了使估计过程更稳健，考虑如下回归问题，并假设贝叶斯方法是其解决方法：

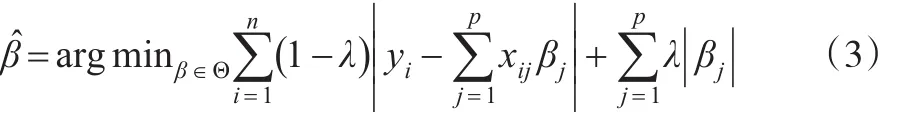
上述最优化问题通过引入惩罚系数λ对损失函数L1以及回归系数惩罚，其中λ∈[ ]0,1。之所以在损失函数L1中加入惩罚项，是考虑到保持模型预测和数据压缩之间的平衡，从而获得较好的稳健估计。当λ=0时，；当λ=1时，

通过边际似然方法，在假设两组超参数以及惩罚参数的先验分布为Laplace先验分布的情况下，得到服从边际似然Laplace先验分布的重尾数据，利用贝叶斯理论得到各参数的后验分布，将这种方法称之为平衡的贝叶斯Lasso（BBLasso）。

首先，为了给每一个参数构建一个具有封闭形式的条件后验分布，所有参数采用如下的全条件分层结构：

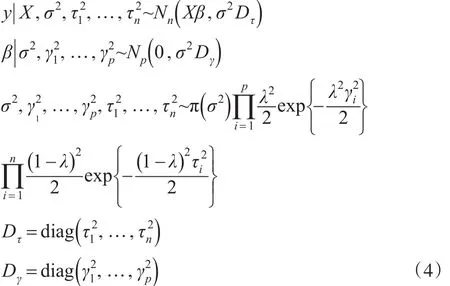
1.2 Gibbs抽样

考虑到在所有参数的先验分布已知的情况下，各参数的全条件分布容易抽样，于是可通过Gibbs抽样来推导出各参数的全条件后验分布。通过边缘优化，去除含有潜变量τ和γ相关的表达式，得到如下的初始边缘贝叶斯模型：

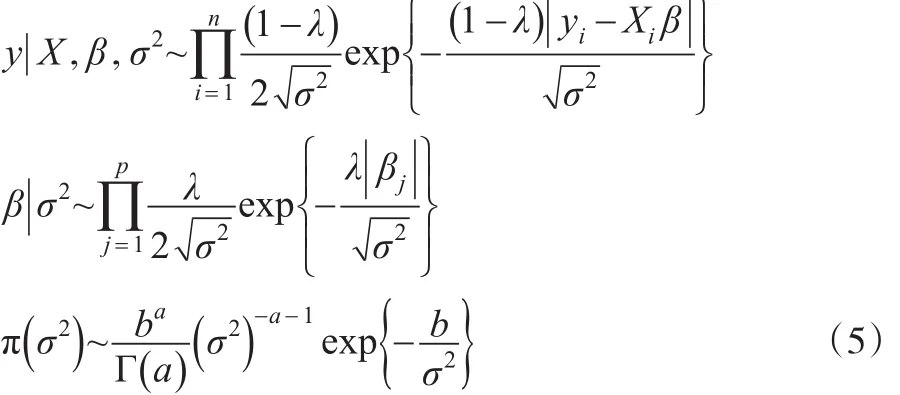
最后推导出β的全条件后验分布服从均值为y,方差为σ2A-1的多元正态分布，其中A=XT。潜变量和的倒数的全条件后验分布服从逆高斯分布，如下是的逆高斯参数：

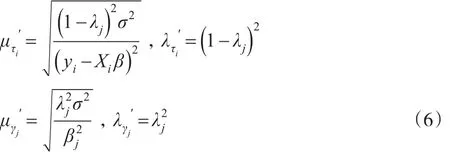
利用共轭性推导出σ2的全条件后验分布服从参数分别为的逆伽

马分布。

2 惩罚参数选择

在频率学派框架下，惩罚参数的选择一般采用交叉验证法进行选择，然而在贝叶斯理论框架下，可以采用全新的办法，比如利用无信息先验分布的假设，从分布中模拟出参数的合理估计值。本文采用两种不同的惩罚函数参数的选择方法。一种方式通过边缘极大似然方法，在基于Gibbs连续抽样的MCEM算法[5]上不断地更新惩罚参数λ，另一种则是通过给定惩罚参数λ合适的先验信息，并且利用MWG（Metropolis within G）算法[6]从其后验分布中不断抽样，从而达到更新惩罚参数λ的目的。

2.1 经验贝叶斯估计

将参数β，τ，γ和λ视为缺失数据，通过边缘极大似然来估计惩罚参数λ，然后通过EM迭代算法来更新惩罚参数，由于边缘极大似然方法涉及到积分运算，当模型维数很高时，很难直接通过积分运算出λ的解析形式。为了解决此问题，采用MCEM算法来估计λ的值。该算法的E-步均采用吉布Gibbs采样，根据M-步可以导出λ(k)的估计值是如下三次多项式的解：

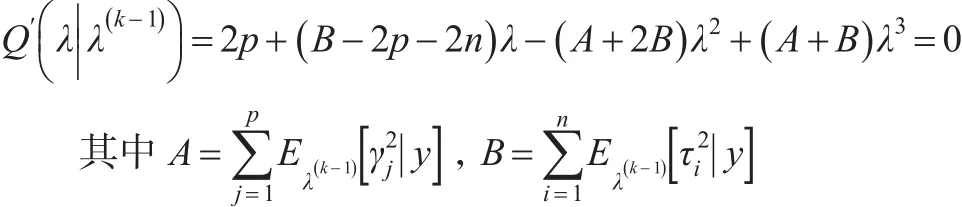
2.2 分层贝叶斯估计

为了得到所有参数的全贝叶斯模型，本文假设λ的先验分布为π(λ)=1，此方法能够在缺少惩罚参数信息时保证λ∈(0 ,1)，并且使得方差部分的后验估计为通常的极大似然估计。使用上述先验时，很难计算出λ的全条件后验分布，但是通过计算推导出λ的全条件后验分布与如下形式的表达式成比例：

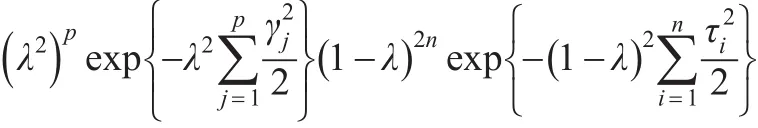
3 数据仿真

通过在不同的仿真情况下比较BBALASSO、LASSO、BLASSO的预测精度和变量选择。LASSO选用Efron提出的5层交叉检验的LARS算法[2]，BLASSO选用Gramacy的BLASSO算法来选择压缩系数[6]。利用R软件来实现BBLASSO的Gibbs采样。

选用如下线性模型：

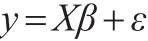
在不同的预测值和误差项分布情形下进行仿真。每一个仿真数据集被分为一个验证集、一个训练集和一个测试集。从验证集中选择LASSO的惩罚参数λj。在选择完惩罚参数之后，混合验证集和训练集来估计LASSO的β。

仿真一：本例中选定系数β=(3,1.5,2,0,0,0,0,0)′，训练集中含有20组观测值，验证集中含有20组观测值，测试集中含有200组观测值。设计矩阵X生成自均值为0，方差为1的多元正态分布，对于所有的i和j，向量xij和xjk的相关系数为0.5|j-k|。这里误差项ε生成自均值为0，方差分别为1，3，5的多元正态分布[7]。

仿 真 二 ：本 例 中 选 定 系 数β=(5 .6,5.6,5.6,0)′，j＜k＜4时，cov (xij,xik)=-0.39，j＜4时，cov(xij,xi4)=0.23。其他参数设置与仿真一一致，包括数据集设置[8,9]。

仿真三：本例中选定系数：

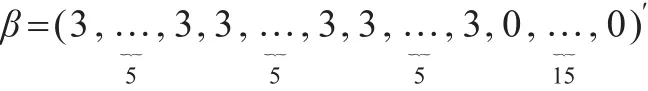
三组相互独立的预测因子P1，P2和P3生成自均值为0，方差为1的多元正态分布。令Xi=P1+εi，i=1,…,5；这里误差项ε生成自均值为0，方差分别为1，3，5，10，15的多元正态分布，训练集中含有100组观测值，验证集中含有100组观测值，测试集中含有400组观测值。

为了模拟出异常值，本文通过将生成的回归矩阵X中的任意一个元素值修改成较大的值，从而可将模型视作存在异常值模型。将仿真一、仿真二及仿真三在不同异常值个数的详细模拟结果分别列于表1、表2及表3中，模拟过程中均选定λ=0.5，迭代10000次，每组比较都将给出不同的预测精度和变量选择效果。

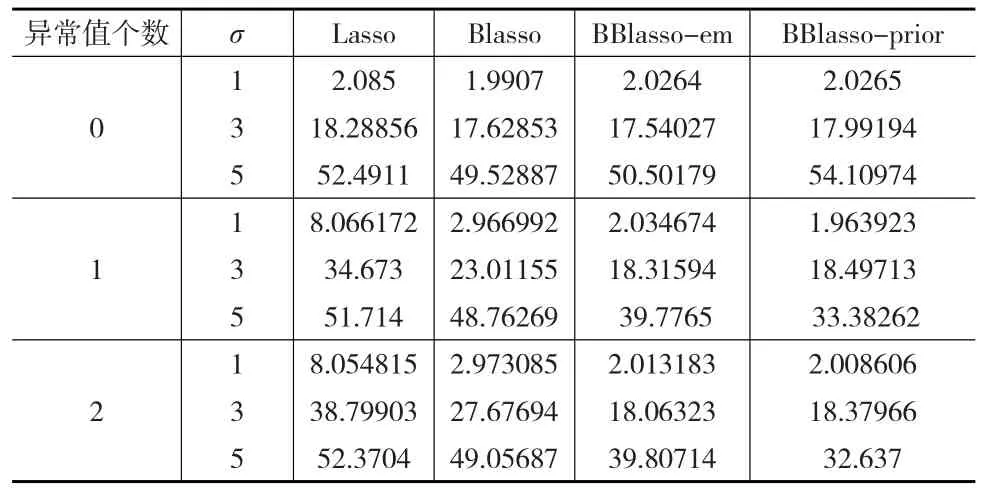
表1 仿真一中四种方法重复50次的预测精度平均值

3.1 预测精度

对四种方法重复50次仿真模拟来比较各个方法的预测精度和变量选择。利用各仿真模拟的预测均方误差（PSEs）平均值来判别各个方法的预测精度。

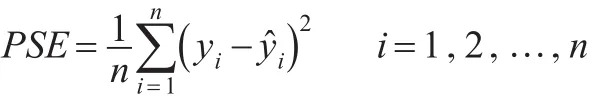
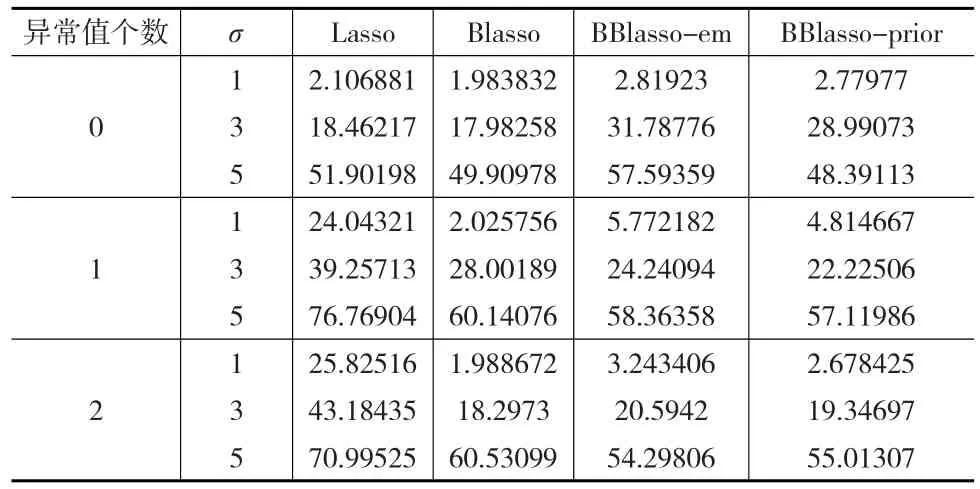
表2 仿真二中四种方法重复50次的预测精度平均值

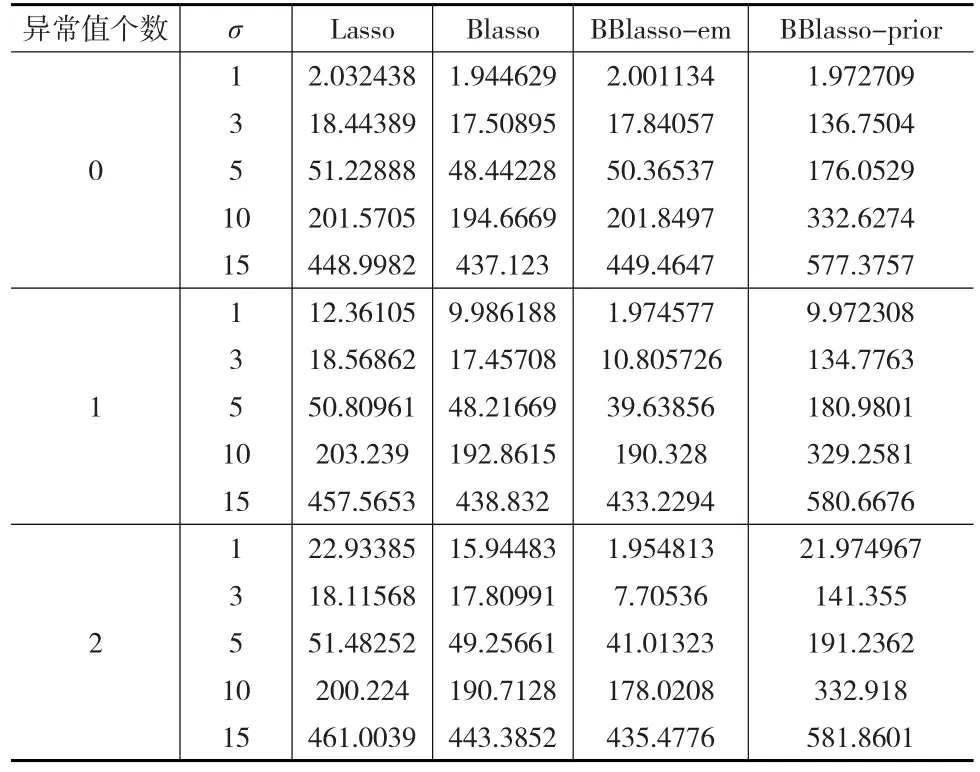
表3 仿真三中四种方法重复50次的预测精度平均值

从表1中可以看出在模型中不论是否存在异常值，Lasso预测精度相对其他三种方法较差。当模型中存在异常值时，BBlasso预测精度明显高于Blasso预测精度，并且可以明显看出在存在异常值模型中，BBlasso的PSEs值几乎一致以及随着方差以及异常值个数的增加，均方误差也随着增加，从而可以印证BBlasso在存在异常值乃至极端异常值的模型中是比较稳健的。

从表2中可以看出仿真二的结果与仿真一几乎一致，结合仿真1与仿真2的模型可以看出BBlasso的两种方法在小样本乃至中等样本中的表现相对其他方法有明显优势。然而在大样本模型中，就不会存在着明显的优势，甚至会相对其他方法较差。

从表3中可以看出，当模型中不存在异常值时，BBlasso-em的预测精度与Lasso以及Blasso相差不大，然而当存在异常值时，BBlasso-em相比其他三种方法的预测精度有明显的优势，BBlasso-prior相对其他三种方法，在预测精度上表现较差。

3.2 变量选择

在多元线性回归问题中，模型变量选择是其重要环节，本文为了比较模型变量选择的好坏，采用ROC（Receiver Operating Characteristic）分析对四种方法的变量选择进行评判，并通过R软件计算AUC值（Area Under Roc Curve）直观地体现各个方法变量选择的效果。AUC值就是处于ROC曲线下方的那部分面积的大小。通常，AUC的值介于0.5到1之间，较大的AUC代表了在变量选择上表现得更好。

这里仅计算了仿真一以及仿真三各方法的AUC值，之所以不计算仿真二的AUC值在于仿真二仅有四个预测因子其中还包括了一个零，计算出来的AUC值不具代表性。对于仿真一以及仿真三的AUC值见表4和表5。

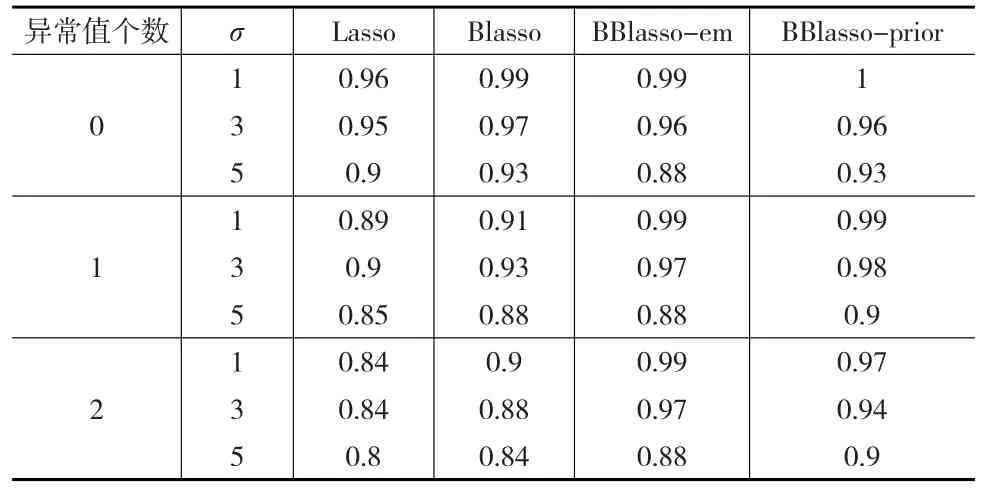
表4 仿真一中四种方法的AUC值

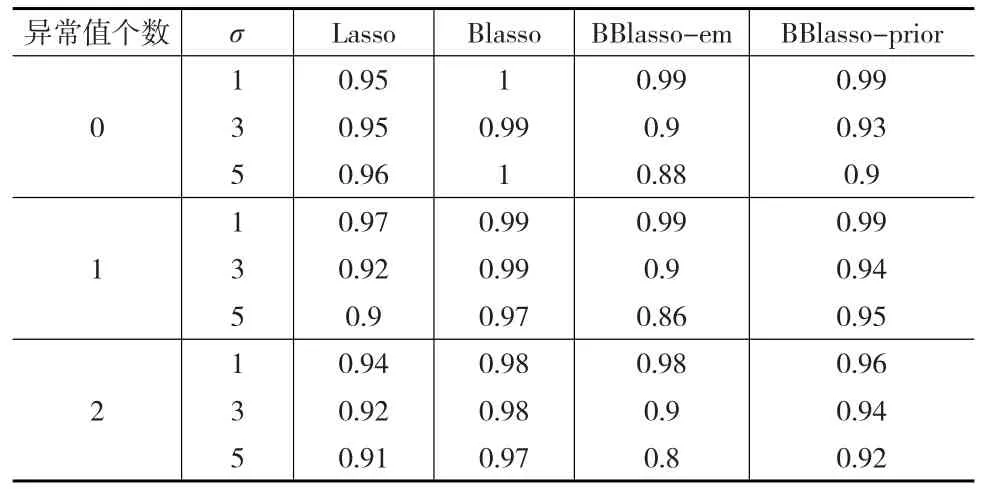
表5 仿真三中四种方法的AUC值

从表4可以看出，在仿真一中，BBlasso-em在模型不存在异常值的情况下，其AUC值与Blasso以及Lasso的AUC值几乎一致，然而当模型存在异常值时,BBlasso-em的AUC值相比Blasso以及Lasso的AUC值有一定的优势。

从表5可以看出，在仿真三中，Blasso的AUC值均比其他方法的AUC值大，然而不得不考虑Blasso方法在未能很好地处理异常值的情况下，所得的AUC值与BBlasso-prior的AUC值相差不大。因此也可以说明BBlasso在很好地处理异常值的情况下，变量选择效果与其他方法相接近。

4 实例分析

4.1 前列腺数据

数据来源于Stamey 等[10]的研究，并在文献[7,9，11]中多次被作为历史数据使用。数据包含97例前列腺癌病例，感兴趣结果变量为PSA水平，8个预测变量分别为：前列腺癌体积、前列腺重量系数、年龄、良性前列腺增生量、精囊入侵、包膜穿透、前列腺评分、前列腺评分4/5所占百分比。本文将67组前列腺数据作为训练集，30组前列腺数据作为测试集。为了判断误差项是否服从正态分布，本文通过K-S检验，得出K-S检验P值为0.7012，其远远大于0.05，可以认为误差项服从正态分布。此外，还通过绘制误差项Q-Q图，见图1，可以看出误差项与正态分布并没有很大的偏差。

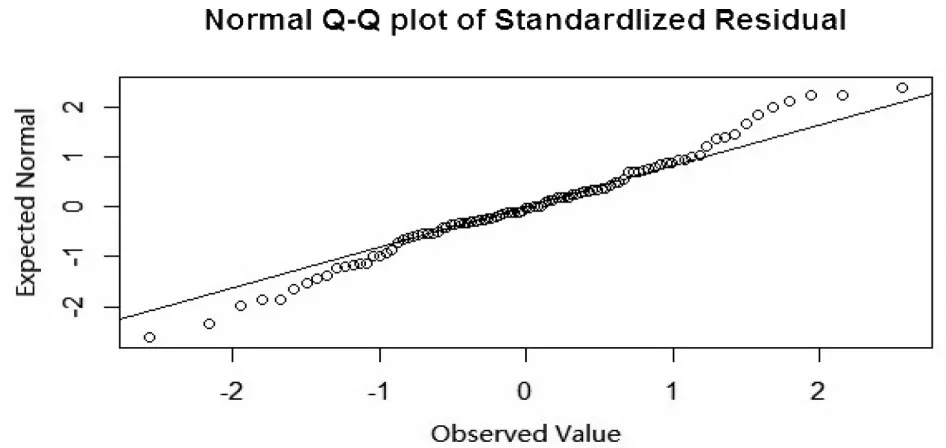
图1 前列腺数据的误差项Q-Q图

通过前列腺数据，研究当误差项服从正态分布的情况下，Lasso、Blasso、Blasso-em、blasso-prior四种方法的预测精度，利用R软件，最终得出四种方法的预测均方误差值(PSE)，见表6。

表6 前列腺数据在四种方法下的PSE值

从表6中可以看出，当数据误差项服从正态分布时，四种方法的预测精度相差不大。

4.2 上证指数与宏观经济指标数据

随着股市不断发展，股市与宏观经济之间的密切关系完全展现出来，为了研究股市与宏观经济之间的关系[12]，本文选取2007年9月1日到2016年9月15日时间段上证指数共3300组数据，每日收盘价Pt作为基础数据，将股指收益作为感兴趣结果变量。一般地,收益率(也称为对数收益率)序列定义为：

1,2,…,其中,P0,Pt分别为初始时刻及t时刻的资产价格。以8个宏观经济指标作为预测变量，宏观经济指标选用工业增加值、货币供应量、年利率、人民币储蓄存款、国内生产总值、股票成交金额、固定资产投资、进出口差额[13]。本文将2300组数据作为训练集，1300组数据作为测试集。为了判断误差项是否服从正态分布，通过K-S检验，得出K-S检验P值远远小于0.05，可以认为误差项不服从正态分布，并通过绘制误差项Q-Q图，见图2，可以看出误差项Q-Q图呈现出重尾现象。

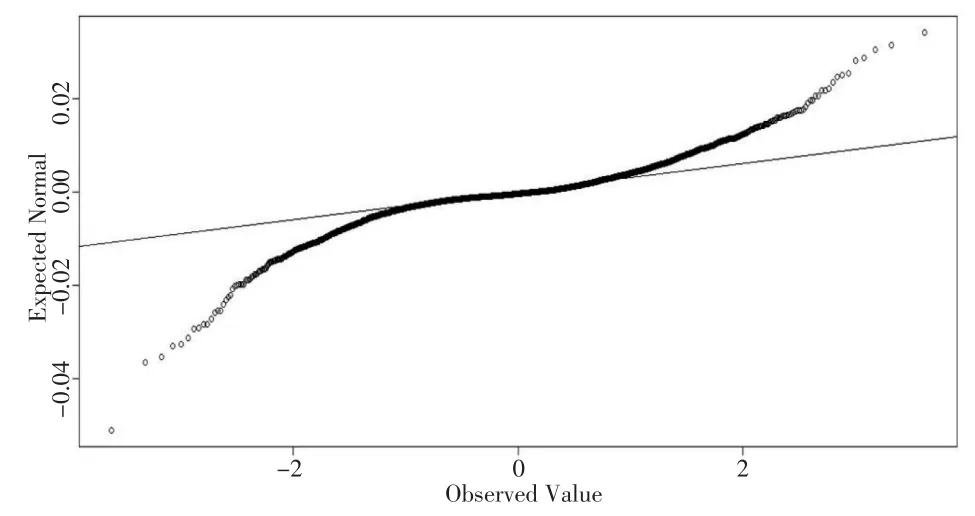
图2 上证指数与宏观经济指标数据的误差项Q-Q图

通过上述数据，研究当误差项服从重尾分布的情况下，Lasso、Blasso、Blasso-em、Blasso-prior四种方法的预测精度，利用R软件，最终得出四种方法的预测均方误差值（PSE），见下页表7。

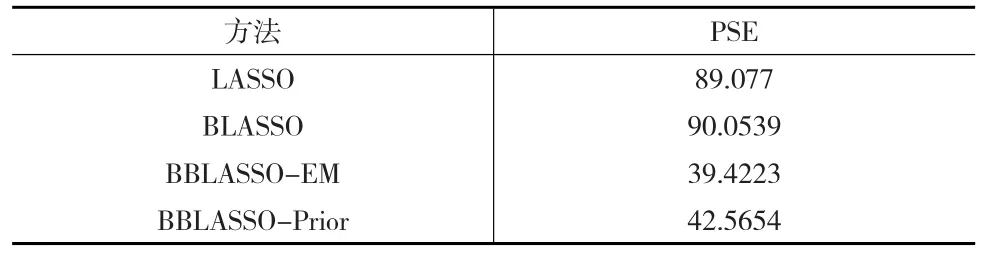
表7 上证指数与宏观经济指标数据在四种方法下的PSE值

从表7中可以看出，在数据误差项服从重尾分布的情况下，LASSO与BLASSO预测精度相差不大，然而相比本文提出的BBLASSO两种方法，还有较大差距。

5 总结

本文在Bayesian Lasso的基础上，引入两组潜变量，从而能够允许模型存在误差，通过选用未知参数以及潜变量合适的先验分布，提出分层模型，并通过Gibbs抽样与边际似然，获得未知参数的后验分布，以及采用不同的惩罚参数结构，来不断地更新惩罚参数。从模拟研究和实例分析可以看出，本文提出的方法相比现有的方法，在模型中存在异常值以及重尾数据的情形下更加精确，并且也可以胜任变量选择。

当然本文也存在一些问题，即假设回归系数先验分布所依赖的条件参数对所有解释变量都是相同的，也即对所有分量选用一样的压缩系数，为此可以进一步研究对不同分量采用不同压缩系数，从而研究出更加有效的估计方法。

参考文献：

[1]Tibshirani R.Regression Shrinkage and Selection Via the Lasso[J].Journal of the Royal Statistical Society,1996,58(1).

[2]Efron B,Hastie T,Johnstone I,et al.Least angle Regression[J].Ann Statist,2004,32(2).

[3]Park T,Casella G.The Bayesian Lasso[J].J Amer Statist Assoc,2008,103(482).

[4]Gramacy R B,Pantaleio E.Shrinkage Regression for Multivariate Inference With Missing Data,and an Application to Portfolio Balancing[J].Bayesian Anal,2010，5(2).

[5]袁晶.贝叶斯方法在变量选择问题中的应用[D].济南：山东大学博士学位论文,2013.

[6]魏艳华,王丙参,孙永辉.分组数据场合Burr-XII分布参数贝叶斯估计的混合Gibbs算法[J].统计与决策,2015,(8).

[7]Li Q,Lin N.The Bayesian Elastic Net[J].Bayesian Anal,2010,5(1).

[8]Zou H.The Adaptive Lasso and Its Oracle Properties[J].J Amer Statist Assoc,2006,101(476).

[9]Leng C,Tran M N,Nott D.Bayesian Adaptive Lasso[J].Ann Inst Statist Math,2014,66(2).

[10]Stamey T A,Kabalin J N,McNeal J E,et al.Prostate Specific Antigen in the Diagnosis and Treatment of Adenocarcinoma of the Prostate.ii.Radical Prostatectomy Treated Patients[J].Journal of Urology，1989,141(5).

[11]Zou H,Hastie T.Regularization and Variable Selection via the Elastic net[J].J R Stat Soc Ser B Statist Methodol,2005,67(2).

[12]尚鹏岳,李胜宏.上证指数与宏观经济指标协整关系的实证分析[J].预测,2002,(4).

[13]王晓燕,吕效国,范玉,张媛.上证指数与宏观经济指标关系的实证分析[J].商业时代,2012,(10).