郭 育 红

(河西学院 数学与统计学院, 甘肃 张掖 734000)

0 引 言

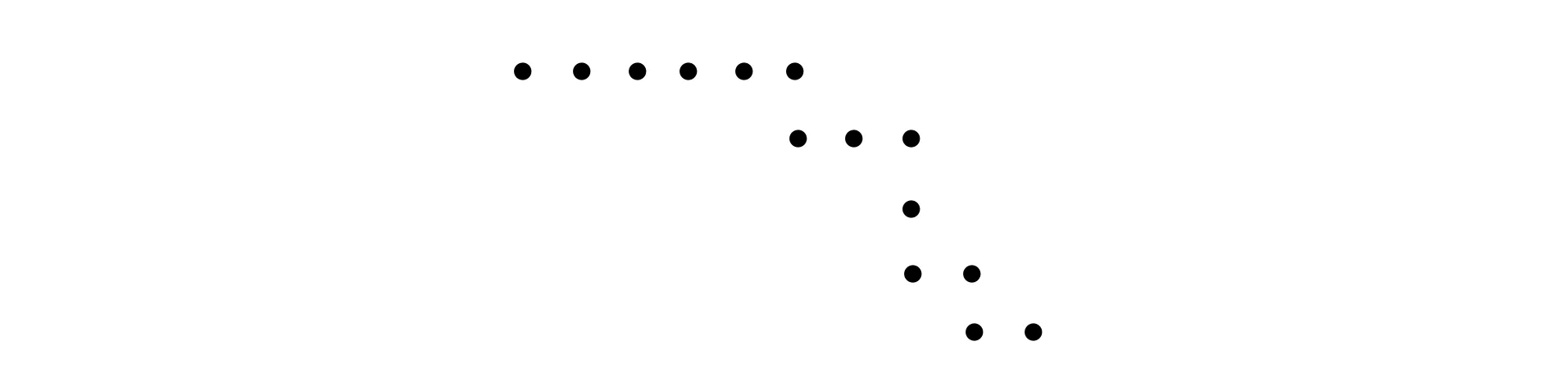
图1 分拆(6,3,1,2,2)的zig-zag图Fig.1 Zig-zag graph of composition (6,3,1,2,2)

整数分拆理论是组合数学研究领域中的一个重要课题, 目前已有很多研究结果[1-2]. 近年来, 关于分部量带约束条件的有序分拆的研究也取得了许多成果[3-7]. 在经典分拆理论中, MacMahon[1]定义了正整数的有序分拆, 即把正整数n表示成一些正整数的有序和, 其中每项称为该分拆的分部量. 例如: 4的有序分拆有4,3+1,1+3,2+2,2+1+1,1+2+1,1+1+2,1+1+1+1, 共8个, 也可记为(4),(3,1),(1,3),(22),(12,2),(1,2,1),(2,12),(14). 文献[1]给出了有序分拆的一些分析性质及图表示, 称为zig-zag图, 类似于无序分拆的Ferres图, 即将有序分拆每个分部量ni依次用一行含有ni个点表示, 但要求下一行的第一个点与上一行的最后一个点对齐. 例如: 分拆(6,3,1,2,2)的zig-zag图如图1所示.

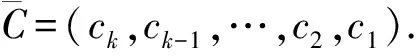
定理1[10]设C≠2(m)表示正整数m的不含分部量2的有序分拆数, 则

C≠2(n)=2C≠2(n-1)-C≠2(n-2)+C≠2(n-3),n>2,

(1)

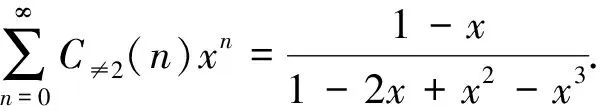
本文进一步研究正整数互为共轭的分拆均不含分部量2的有序分拆, 给出该类有序分拆数与Fibonacci数之间的一个关系式, 并结合正整数的分部量是1,2, 分部量是奇数, 分部量大于1的有序分拆与Fibonacci数之间的关系式, 得到这几类有序分拆数之间的几个分拆恒等式, 并给出其组合证明. 本文用CC≠2(n)表示正整数n的互为共轭分拆均不含分部量2的有序分拆数.

1 主要结果

由于正整数7的有序分拆(5,1,1)的共轭分拆是(1,1,1,1,3), 所以(5,1,1) 即为本文所研究的有序分拆, 而分拆(3,4)的共轭分拆是(1,1,2,1,1,1), 含有分部量2, 所以(3,4)不是本文所讨论的有序分拆. 首先给出这种有序分拆数的递推关系式.

定理2设CC≠2(n)表示正整数n互为共轭的分拆均不含分部量2的有序分拆数, 则

CC≠2(1)=1,CC≠2(2)=0,CC≠2(3)=2,CC≠2(4)=2,

(2)

CC≠2(n)=CC≠2(n-1)+CC≠2(n-2),n>4.

(3)

证明: 因为有序分拆及其共轭分拆总成对出现, 故本文仅考虑左端分部量是1的有序分拆. 互为共轭的分拆均不含分部量2的有序分拆, 若左端的分部量是1, 则最少含有两个1. 下面分两种情形讨论：

1) 左端分部量是“1,1”;

在情形1)中, 对于n的任何一个适当的有序分拆, 先删掉左端两个分部量“1,1”, 得到分拆α, 然后求α的共轭分拆α′, 则α′即为n-2的左端分部量是1的相应有序分拆. 反之, 对于n-2的左端分部量是1的适当有序分拆β, 先求其共轭分拆β′, 再在β′的左端添上两个分部量“1,1”, 于是即得到n的左端分部量是“1,1”的相应有序分拆.

在情形2)中, 对于n的任何一个适当的有序分拆, 删掉左端的一个分部量1即得到n-1的左端分部量是1的相应有序分拆. 反之亦然.

由于1符合条件的有序分拆是(1), 2符合条件的有序分拆没有, 3符合条件的有序分拆是(1,1,1),(3), 4符合条件的有序分拆是(1,1,1,1),(4), 故结论成立. 证毕.

表1列出了部分正整数互为共轭的分拆均不含分部量2的有序分拆数.

表1 互为共轭的分拆均不含分部量2的有序分拆数

数列CC≠2(n)与数列A006355相同[11], 而序列A006355也表示n-pan图的匹配数. 由上述递推关系易得如下推论.

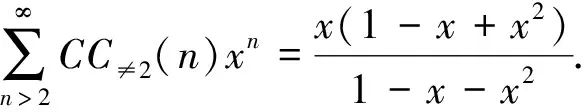
推论2若CC≠2(n)表示正整数n的互为共轭的分拆均不含分部量2的有序分拆数, 则

CC≠2(n+2)=2Fn,n>0.

(4)

由于正整数n的分部量是奇数的有序分拆数等于Fn, 正整数n的分部量是1,2的有序分拆数等于Fn+1, 正整数n的分部量大于1的有序分拆数等于Fn-1, 因此易得正整数n的互为共轭的分拆均不含分部量2的有序分拆数与上述几类有序分拆数之间的分拆恒等式. 因为有序分拆及其共轭有序分拆总是成对出现, 故本文仅给出左端分部量是1的组合证明, 左端分部量大于1的证明类似.

定理3设C>1(n)表示正整数n的分部量大于1的有序分拆数, 则

CC≠2(n+1)=2C>1(n),n>1.

(5)

证明: 对于正整数n+1的互为共轭的分拆均不含分部量2, 且左端分部量是1的任意一个有序分拆α, 首先求α的共轭分拆α′, 此时α′左端的第一个分部量h>2, 且两个大于2的分部量之间至少有一个分部量1; 其次, 在α′中按照从左向右的顺序将分部量1右边大于2的分部量d分拆成“1,d-1”, 然后仍按照从左向右的顺序将相邻的分部量“1,1,…,1”相加产生新的分部量, 即得到分拆β； 最后, 将分拆β左端的第一个分部量h用h-1代替, 得到有序分拆γ, 则γ即为n的分部量大于1的有序分拆.

反之, 对于n的任意一个分部量大于1的有序分拆γ=(λ1,λ2,…,λt), 首先把第一个分部量λ1用λ1+1替换, 按照从左向右的顺序, 依次将λ2分拆成“1,1,…,1”,λ3不变,λ4分拆成“1,1,…,1”,λ5不变, 以此类推直到λt, 即得到分拆δ; 其次, 对于δ按照从右向左的顺序, 将大于1的分部量h与其左边的一个1相加作为新的分部量得到有序分拆β, 此时,β是任意两个大于1的分部量之间至少有一个分部量1; 最后求β的共轭分拆β′, 则β′即为n+1的左端第一个分部量是1, 且分拆及其共轭分拆均不含分部量2的有序分拆.

例如, 14的有序分拆(1,1,3,1,1,1,3,1,1,1)产生13的分拆(2,2,4,2,3)过程如下：

反之,

故结论成立. 证毕.

下面举例说明定理3中的分拆恒等式.

例1当n=7时, 8的互为共轭的分拆均不含分部量2的有序分拆与7的分部量大于1的有序分拆之间的对应关系为:

(1,1,1,1,1,1,1,1)↔(7)↔(8), (1,1,6)↔(2,5)↔(3,1,1,1,1,1),

(1,1,1,1,1,3)↔(5,2)↔(6,1,1), (1,1,1,1,4)↔(4,3)↔(5,1,1,1),

(1,1,1,5)↔(3,4)↔(4,1,1,1,1), (1,1,1,3,1,1)↔(3,2,2)↔(4,1,3),

(1,1,4,1,1)↔(2,3,2)↔(3,1,1,3), (1,1,3,1,1,1)↔(2,2,3)↔(3,1,4).

定理4设C1-2(n)表示正整数n的分部量是1,2的有序分拆数, 则

CC≠2(n+3)=2C1-2(n),n>0.

(6)

证明: 对于正整数n+3的互为共轭的分拆均不含分部量2, 且左端分部量是1的任意一个有序分拆α, 由定理3的证明可得n+2 的分部量大于1的有序分拆β. 下面求β的共轭分拆β′. 因为β是分部量大于1的有序分拆, 所以其共轭分拆β′即为分部量是1,2, 且左右两端的分部量都是1的有序分拆. 将β′的左右两端各删掉一个分部量1, 即得到n的分部量均为1,2的有序分拆. 由定理3的证明以及上述对应法则可知, 该对应关系是可逆的. 证毕.

定理5设Codd(n)表示正整数n的分部量是奇数的有序分拆数, 则

CC≠2(n+2)=2Codd(n),n>0.

(7)

证明: 对于正整数n+2的互为共轭的分拆均不含分部量2, 且左端分部量是1的任意一个有序分拆α, 由定理3的证明可得n+1的分部量大于1的有序分拆β. 下面求β的共轭分拆β′. 因为β是分部量大于1的有序分拆, 所以其共轭分拆β′即为分部量是1,2, 且左右两端的分部量都是1的有序分拆. 将β′的左端删掉一个分部量1, 再按照从右向左的顺序将1及其左边相邻的所有2相加产生新的分部量, 于是得到n的分部量均为奇数的有序分拆. 由定理3的证明以及上述对应法则可知, 该对应关系是可逆的. 证毕.

下面举例说明定理5中的分拆恒等式.

例2当n=6时, 8的互为共轭的分拆均不含分部量2的有序分拆与6的分部量是奇数的有序分拆之间的对应关系为:

(1,1,1,1,1,1,1,1)↔(1,1,1,1,1,1)↔(8), (1,1,6)↔(3,1,1,1)↔(3,1,1,1,1,1),

(1,1,1,1,1,3)↔(1,1,1,3)↔(6,1,1), (1,1,1,1,4)↔(1,1,3,1)↔(5,1,1,1),

(1,1,1,5)↔(1,3,1,1)↔(4,1,1,1,1), (1,1,1,3,1,1)↔(1,5)↔(4,1,3),

(1,1,4,1,1)↔(3,3)↔(3,1,1,3), (1,1,3,1,1,1)↔(5,1)↔(3,1,4).

在整数分拆理论中, 分部量带约束条件的分拆一直是该领域的研究热点, 尤其是寻找各类有序分拆数之间的分拆恒等式, 建立不同类型分拆之间的组合双射具有重要的理论意义. 本文借助一些特殊的有序分拆数与Fibonacci数之间的关系式, 给出了正整数的互为共轭的分拆均不含分部量2的有序分拆数与分部量大于1的有序分拆数, 分部量是1,2的有序分拆数, 分部量是奇数的有序分拆数之间的分拆恒等式以及组合证明, 进一步丰富了整数分拆理论.

衷心感谢审稿专家提出的宝贵意见.

[1] MacMahon P A. Combinatory Analysis: Volumes 1 [M]. Mineola, NY: Dover Publications, Inc, 1915.

[2] Andrews G E. The Theory of Partitions [M]. Cambridge: Cambridge University Press, 1998.

[3] 郭育红, 王汝军. 与自反的n-Color有序分拆相关的一些恒等式 [J]. 数学学报(中文版), 2016, 59(4): 535-544. (GUO Yuhong, WANG Rujun. Some Identities Related to the Self-inversen-Color Compositions [J]. Acta Mathematica Sinica (Chinese Series), 2016, 59(4): 535-544.)

[4] Shapcott C. New Bijections fromn-Color Compositions [J]. J Comb, 2013, 4(3): 373-385.

[5] Shapcott C. C-Color Compositions and Palindromes [J]. Fibonacci Quart, 2012, 50(4): 297-303.

[6] GUO Yuhong. Inverse-Conjugate Compositions with Odd Parts [J]. Ars Comb, 2017, 135: 93-102.

[7] GUO Yuhong.n-Color Odd Self-inverse Compositions [J/OL]. J Integer Seq, 2014-11-04. https://cs.uwaterloo.ca/journals/JIS/VOL17/Guo/guo9.pdf.

[8] Munagi A O. Primary Classes of Compositions of Numbers [J]. Ann Math Inform, 2013, 41： 193-204.

[9] Munagi A O. Zig-Zag Graphs and Partition Identities of A.K.Agarwal [J]. Ann Comb, 2015, 19(3): 557-566.

[10] Chinn P, Heubach S. Integer Sequence Related to Compositions without 2’s [J/OL]. J Integer Seq, 2003-07-08. https://cs.uwaterloo.ca/journals/JIS/VOL6/Heubach/heubach5.pdf.

[11] Sloane N J A. The On-line Encyclopedia of Integer Sequences [J]. Notices Amer Math Soc, 2003, 50(8): 912-915.