李停

（铜陵学院经济学院，安徽铜陵244000）

0 引言

现实中生活中的企业决策，无论是产量、价格、广告、研发都不再是孤立无关的，而是彼此间存在策略依存和策略互动。尤其是对生产日趋集中的寡占市场，企业任何行动都必须考虑其竞争对手的反应，传统决策理论和运筹学方法很难解决这类利益相互影响的决策均衡问题。博弈论正是研究在利益相互影响的局势中，局中人如何选择自己的策略才能使自身的收益最大化的均衡问题[1]。近半个世纪以来，博弈论的理论和方法激起管理学家的极大兴趣，将决策理论的发展推向前所未有的新高峰。纳什均衡是博弈论最核心的概念，由于战略管理本质上也是组织如何在相互影响的对局中寻求决策均衡的问题，所以本文不加区分地使用纳什均衡和决策均衡的概念。

Nash（1950）[2]应用数学上的不动点定理，证明了“任何有限的策略型博弈至少存在一个混合纳什均衡”。随后，Debreu（1952）[3]给出了“在n个局中人的策略型博弈中，满足局中人策略空间Si是欧式空间的非空有界闭集、支付函数Ui(s)连续且对Si是拟凹函数，该博弈存在一个纯策略纳什均衡”。这是博弈论学科发展过程中的两大理论基石，解决了均衡的存在性问题。国内学者中，李正龙（2001）[4]、朱年磊等（2006）[5]对静态博弈纯策略纳什均衡的存在性作了延伸性探讨。但从实践应用角度看，如何寻求纳什均衡同样不容忽视。现有文献大致可梳理出博弈均衡的三种求解方法：相对优势划线法、期望支付等值法和最优反应函数法。这些方法不同程度地存在适用范围有限、过程繁琐等弊端。如何寻求一种归一化解法，将复杂的纳什均衡求解过程“简单化、程序化和规范化”，正是本文的写作目的。本文将在理论上证明，局中人的支付矩阵在局部变换下不改变博弈的均衡特征，并以纳什均衡不变性定理为基础，完成16种类型的2×2型博弈决策均衡的归一化求解。

1 2×2型博弈构成要素及均衡表述

1.1 2×2型博弈的构成要素

对于完全信息的静态博弈，策略型博弈模型是较为适当的表示，而局中人、策略和支付是构成策略型博弈的三个基本要素。本文分析的2×2型博弈是指包含2个局中人，每个局中人只有2个策略的有限博弈。2×2型博弈构成要素虽然简单，但却是分析N个局中人复杂博弈的基础。从纯粹数学意义上讲，这无非是2维向量空间向N维向量空间的形式化推广。

于是G=(2,S1,S2,u1,u2)为2×2型博弈的策略型表示，S1、S2分别是局中人1、2的策略空间。在2×2型博弈中，S1、S2都只含有2个元素，记

令s1、s2是局中人1、2具体的某个策略，s1∈S1，s2∈S2。u1、u2代表局中人1、2在各种策略组合下的支付。由于局中人和策略都是有限集，2×2型博弈的策略组合也是有限集，策略组合空间可表示为

由于分析的是完全信息静态博弈，策略等同于行动。记局中人1的行动集为α={α1,α2}，局中人2的行动集为β={β1,β2}。再记u1(αi,βj)=aij，u2(αi,βj)=bij，i=1,2，j=1,2。该2×2型博弈的支付矩阵如表1所示：为下文分析方便，记表示局中人1、2的支付矩阵。

表1 2×2型博弈的支付矩阵

1.2 2×2型博弈的均衡表述

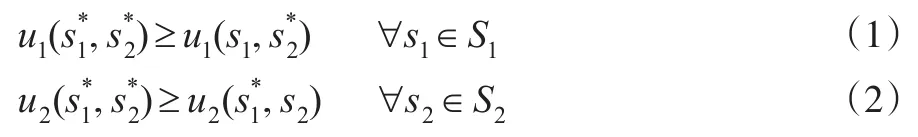
由于并非所有2×2型博弈都有纯策略纳什均衡，需引入混合纳什均衡的概念。局中人1的混合策略X=[p,1-p]表示分别以概率p、1-p选择行动α1、α2。局中人2的混合策略Y=[q,1-q]T表示分别以概率q、1-q选择行动β1、β2。利用支付矩阵A和B，局中人1、2的期望支付的代数表示为E1(X,Y)=XAY、E2(X,Y)=XBY。这里X表示局中人1的混合策略行向量，Y表示局中人2的混合策略列向量。混合策略(X*,Y*)为G的混合纳什均衡，当且仅当X*AY*≥XAY*、X*BY*≥X*BY对任何X、Y同时成立。易知当p=1或p=0时，局中人1的混合策略e1=(1,0)、e2=(0,1)退化成纯策略α1、α2；同样，当q=1或q=0时，局中人2的混合策略e1=(1,0)、e2=(0,1)退化成纯策略β1、β2。因而混合策略包含着纯策略的含义，对二者的分析便可以统一起来。

2 纳什均衡的不变性

2.1 纳什均衡不变性定理

定理1：设G=(2,S1,S2,u1,u2)为某2×2型博弈，则纳什均衡对任一局中人的支付函数的正仿射变换下不变。即对i∈{1,2}，令(s)=σiui(s)+εi，其中σi＞0。正仿射变换下的新2×2型博弈与G有相同的纳什均衡。

定理2：纳什均衡在支付函数的局部变换下不变。

2.2 纳什均衡不变性定理的实质

定理1和定理2使用严谨而又晦涩的数学语言诠释纳什均衡的不变性。事实上，借助局中人支付矩阵A和B对该定理简化，有助于把握纳什均衡不变性定理的实质。

对G的支付函数作正仿射变换，相当于对局中人1、2的支付矩阵A、B的每个元素乘以一个正数再加上一个常数。即A′=σ1A+ε1，B′=σ2B+ε2，其中，σ1,σ2＞0，εi是元素取值为常数的2阶方阵。

对G的支付函数作局部变换，相当于对A的某一列加一个常数，或者对B的某一行加一个常数。即或者

3 2×2型博弈的决策均衡

3.1 局中人支付矩阵的对角化

既然对支付函数的局部变换实质是对局中人支付矩阵的列或行加某个常数，那么一个自然的想法是只要常数选取得当，很容易将局中人的支付矩阵对角化。这将使得纳什均衡求解过程得到简化，以此为基础可探讨2×2型博弈决策均衡的归一化解法，同时纳什均衡不变性定理保证了这种探讨的有效性。

对局中人1的支付矩阵A进行列变换，将其变成对角阵A′，具体过程如式（3）所示；对局中人2支付矩阵B进行行变换，将其变成对角阵B′，具体过程如式（4）所示：

由于任一2×2型博弈都可通过局部变换成对角阵，下文对其决策均衡的讨论只需对支付矩阵是的2×2型博弈进行。

3.2 局中人的最优反应函数

3.2.1 局中人1的最优反应函数

局中人1的混合策略为X=(p,1-p)，局中人2的混合策略为Y=(q,1-q)T。局中人1的最优反应是对不同的Y，选择X最大化期望支付E1(p,q)。

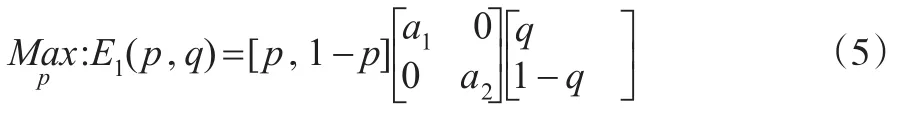
（1）a1＞0，a2＜0。当a1+a2＞0时，恒有此时，对∀q∈[0,1]，p=1最大化期望支付E1；而当a1+a2＜0时，显然成立，从而也得到综合起来，局中人1的最优反应函数：p(q)=1，∀q∈[0,1]。

（2）a1＜0，a2＞0。类似情形（1），可得到此时恒有，故局中人1的最优反应函数：p(q)=0，∀q∈[0,1]。

（3）a1＞0，a2＞0。当时，恒成立。∀p∈[0,1]，都能最大化期望支付E1；当时，，局中人1的最优反应是p(q)=0；当时，，局中人1的最优反应是p(q)=1。局中人1的反应函数可用分段函数表示：

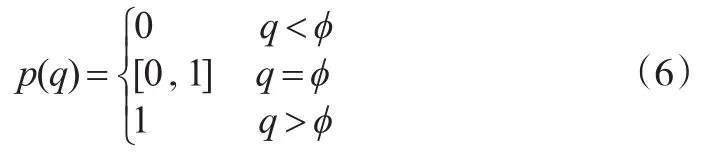
（4）a1＜0，a2＜0。类似情形（3），可得局中人1的最优反应函数：

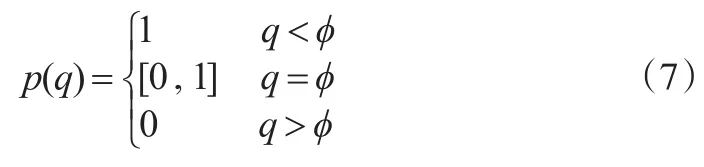
3.2.2 局中人2的最优反应函数

局中人2的最优反应是对不同的X，选择Y最大化期望支付E2(p,q)。

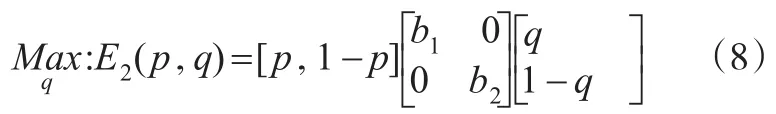
（1）b1＞0，b2＜0。局中人2的最优反应函数：q(p)=1，∀p∈[0,1]。

（2）b1＜0，b2＞0。局中人2的最优反应函数：q(p)=0，∀p∈[0,1]。

（3）b1＞0，b2＞0。局中人2的最优反应函数可用分段函数式（9）表示：

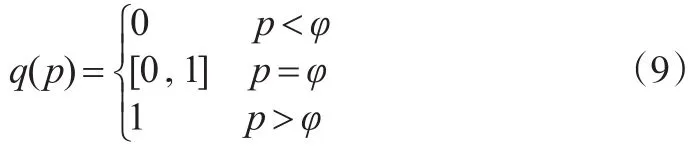
（4）b1＜0，b2＜0。局中人2的最优反应函数可用分段函数式（10）表示：

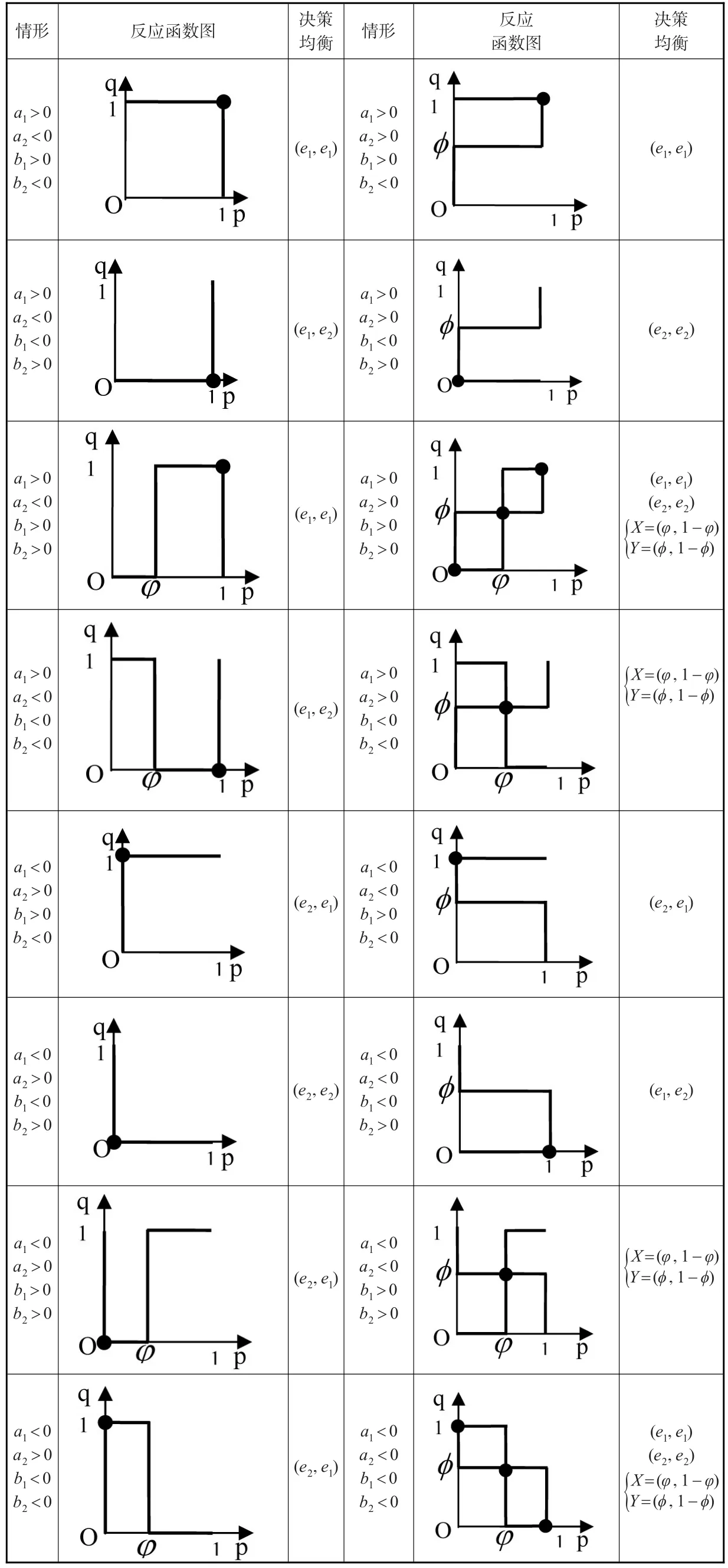
表2 2×2型博弈的决策均衡

3.3 决策均衡

由于局中人1和2的反应函数都有4种情形，交叉组合后共有4×4=16种情形。上页表2列出2×2型博弈在每种情形下的反应函数图形和决策均衡。表2中(ei,ej)是纯策略纳什均衡，如(e1,e2)表示[(1,0),(0,1)]，亦即纯策略组合(α1,β2)。粗实线表示相应的反应函数曲线。

4 算例分析及方法比较

以企业管理中著名的“协调”博弈为例，阐述不同决策均衡求解过程并进行方法比较。企业1和企业2是相关行业内的两个厂商，都具备生产产品甲和乙的技术条件。比较而言，厂商1在产品甲生产上有比较优势，厂商2在产品乙生产上有比较优势。但由于生产过程中的技术互补的原因，两家企业生产同一种产品更容易获得外部规模经济。现在的问题是，两家企业如何协调，实现产品选择决策均衡。表3列出各种策略组合下的支付。

表3 产品选择“协调”博弈

4.1 相对优势划线法

相对优势划线法的基本思想是：对每个局中人在对手各种确定的策略情形下寻求其最优策略，并在该局中人相应的支付下面划一短线。等两个局中人都分析完成后，每个局中人支付下面都有短线的策略组合就是纳什均衡。

对于企业1而言，给定企业2选择产品甲，选择产品甲支付是3，选择乙支付是-1，于是在(3,2)中局中人1的支付3下面划线。类似这样的讨论对所有局中人的全部策略，划线结果也在表3中同时给出。通过相对优势划线法，容易得到该产品选择“协调”博弈的决策均衡是（产品甲，产品甲）、（产品乙，产品乙）。

相对优势划线法的优点是简单易行，但只适用于纯策略纳什均衡的求解。

4.2 期望支付等值法

期望支付相等是混合纳什均衡的一个重要性质。如果(X*,Y*)是博弈G的一个纳什均衡，这里X=[p,1-p]表示局中人1以概率p、1-p选择行动α1、α2，Y=[q,1-q]T表示分局中人2以概率q、1-q选择行动β1、β2，那么E1(X*,Y*)=E1(X,Y*)、E2(X*,Y*)=E2(X*,Y)对任意X、Y都成立。给定某局中人选择均衡策略，另一局中人无论选择什么混合策略都不改变其支付。在混合纳什均衡点上，局中人的期望支付与另一局中人的策略选择无关。这当然也包括两种纯策略，由此引入求解2×2型博弈混合纳什均衡的一种简便方法——期望支付等值法。

仍以产品选择“协调”博弈为例，说明期望支付等值法的求解过程。对于企业1而言，当企业2选择混合策略(q,1-q)时，其选择纯策略产品甲和产品乙的期望支付相等，即：

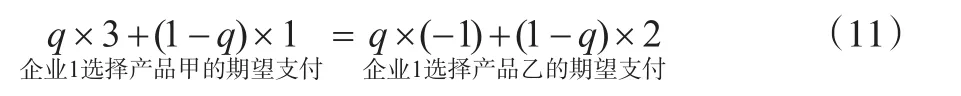
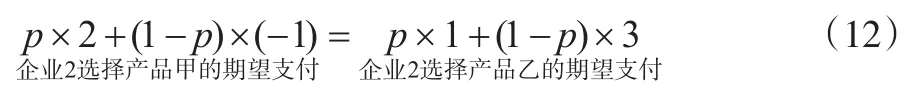
4.3 归一化解法

相对优势划线法和期望支付等值法分别在求解2×2型博弈的纯策略纳什均衡和混合策略纳什均衡方面有各自优势，但缺陷是适用范围有限，容易造成解得遗漏。一个自然的想法是如何将两种方法归一化，探求对2×2型博弈的一般性求解方法。

归一化解法基于最优反应函数法，能有效减轻该方法在使用过程中的计算量。由表3，产品选择“协调”博弈中局中人1、2的支付矩阵是：经局部变换后的对角阵分别是：于是a1=4、a2=1、b1=1、b2=4，。查阅表2知该2×2型博弈有三个纳什均衡：，分别是纯策略纳什均衡（产品甲，产品甲）、（产品乙，产品乙）和混合纳什均衡

通过方法比较后不难发现，2×2型博弈决策均衡的归一化解法利用纳什均衡不变性定理，可将复杂的求解过程“简单化、程序化和规范化”，具有普适性特征，且很好地解决了其他方法解的遗漏问题。

[1]王文举.经济博弈论基础[M].北京：高等教育出版社,2010.

[2]Nash J.Equilibrium Points in n-person Games[J].Proceedings of the National Academy of Science,1950,(36).

[3]Debreu D A.Social Equilibrium Existence Theorem[J].Proceedings of the National Academy of Science,1952,(38).

[4]李正龙.双人静态博弈纯战略纳什均衡存在性判别[J].应用数学与计算机学学报,2001,15(1).

[5]朱年磊,李荣生.静态博弈纯战略均衡存在性判别法[J].曲阜师范大学学报,2006，32(1).