分数阶Froude摆系统的混沌同步
2018-02-13王东晓
王东晓
(郑州航空工业管理学院 理学院,河南 郑州 450015)
整数阶混沌系统是我们熟悉的系统,而实际系统,很多是分数阶次的,有分数阶特性的对象,采用分数阶来描述,能够更好的揭示其行为和本质,分数阶混沌系统引起众多科研工作者的兴趣,分数阶系统的同步问题倍受关注,且已经取得了很多相关成果[1-4]。文献[5]同步了分数阶摩擦系统,文献[6]对时滞分数阶PD控制器设计问题加以研究,文献[7]则反馈同步了分数阶Van der pol-Duffling系统,文献[8]在有限时间内,保证了分数阶混沌系统的鲁棒镇定。而Froude摆系统是典型的二阶非自治系统,在特别的参数设置下系统呈现混沌态,Froude摆系统的同步问题引起了控制界的广泛关注,例如:文献[9]研究了外力激励下Froude摆系统产生混沌的机理问题,文献[10]研究了两个Froude摆系统的暂态阶梯混沌同步控制问题,文献[11]研究了Froude摆系统的全局有限时间同步问题,基于有限时间稳定性理论,有限时间内全局同步两个Froude摆系统。本文基于终端滑模控制研究了分数阶Froude摆系统的同步问题,以Lyapunov稳定性理论和分数阶微积分的相关理论为理论基础,得出了取得系统同步的充分条件。
1 主要结果
1.1 控制方案一
定义1[12]:Caputo分数阶导数定义为:
考虑如下一类分数阶Froude混沌系统:
(1)
当α=0.35,β=0.1,δ=1.0,f=0.42,ω=1.0,q=0.873时系统呈现混沌态。
系统(1)其对应的响应系统为:
(2)
定义系统误差e1=y1-x1,e2=y2-x2,对应误差系统为:
(3)
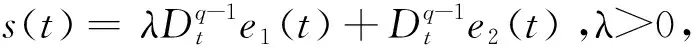
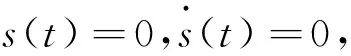

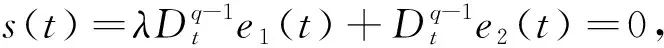
结合e2(t)→0,从而e1(t)→0

=-η|s(t)|<0
由Lyapunov稳定性理论,系统状态轨迹滑向滑模面,综上所述系统(3)在零点稳定,驱动系统(1)与响应系统(2)是滑模混沌同步的,定理得证。
1.2 控制方案二
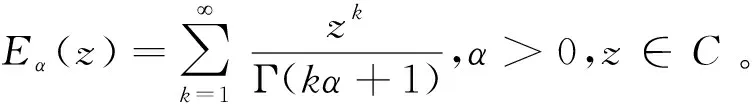
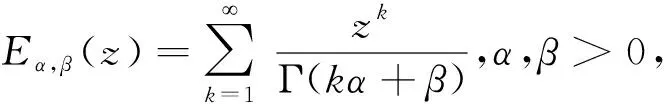
Eα(z)=Eα,1(z),E1,1(z)=ez。
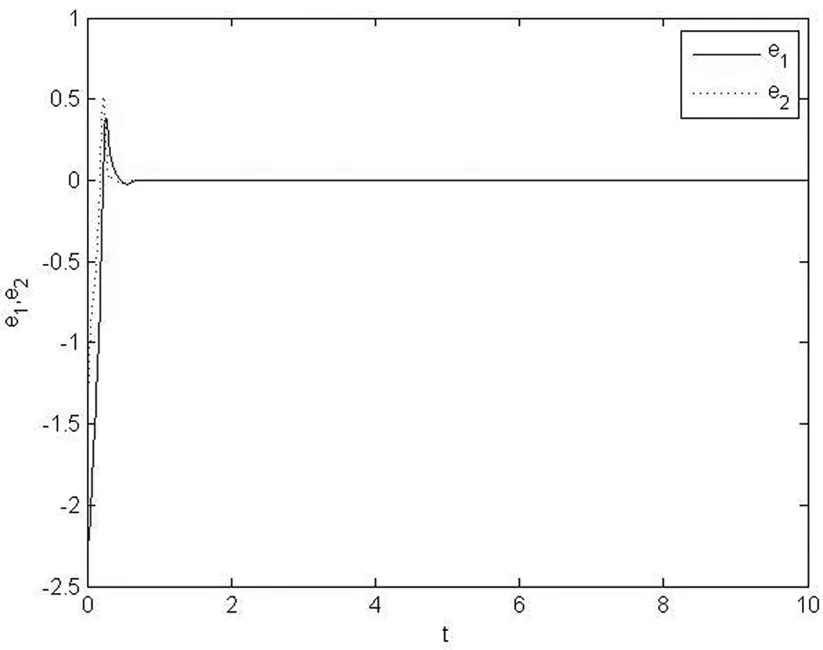
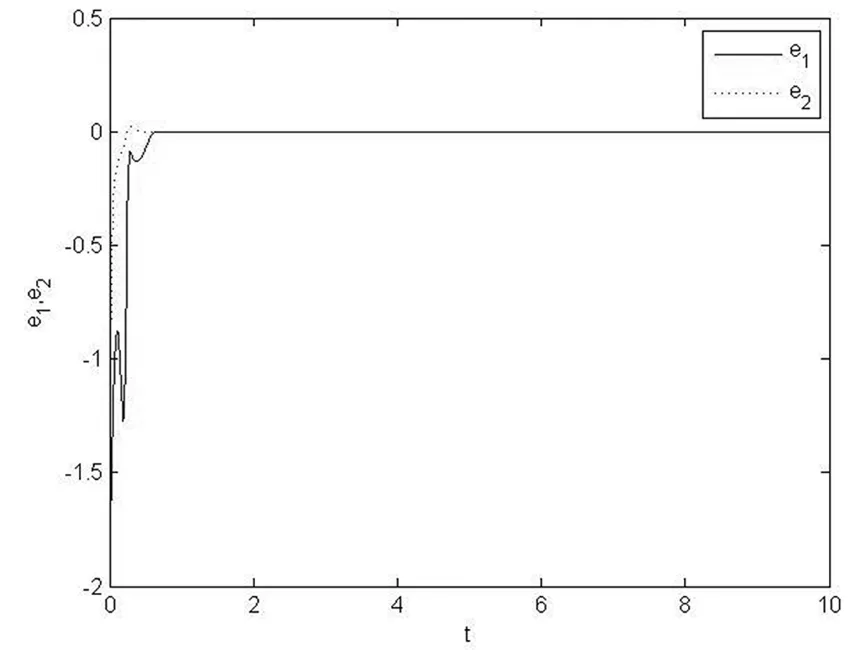
引理1[13]:若α<2,β∈∀R,πα/2<ρ |Eα,β(z)||arg (z)|π),|z|>0。 引理2[14]:若V(t)是[0,)上的连续函数,满足DαV(t)-ηV(t),则有: V(t)V(t0)Eα(-η(t-t0)α),其中α∈(0,1),η>0为常数。 定理2:驱动系统(1)、响应系统(2)是混沌同步的,当选取如下控制器时。 证明:无妨设e1≥0,选取Lyapunov函数V(t)=|e1(t)|+|e2(t)|,求分数阶导数很容易得到: 由sign(e1(t))sign(e2(t))e2(t)=sign(e1(t))|e2(t)|,再e2(t)≠0,sign(e2(t))sign(e2(t))=1,得到: 根据引理2很容易得到:V(t)V(t0)Eα(-(t-t0)q) V(t)=|e1(t)|+|e2(t)|,V(t0)=|e1(t0)|+|e2(t0)| 令z=-(t-t0)q,|arg (z)|=π,根据引理1,存在常数C使得: ‖V(t)‖ 当t→时‖V(t)‖→0,有‖ei(t)‖(i=1,2)→0,驱动系统响应系统实现同步,定理得证。 针对误差系统(3)设计非奇异终端滑模面 (4) 定理3:当系统(3)在滑模面(4)上时,系统状态变量在有限时间内趋于稳定,轨迹达到平衡点。 由Lyapunov稳定性理论,定理得证。 同样的滑模面下,设计新型双幂次趋近律来设计控制律也可以实现系统同步。 定理4:设计如下控制器(5) (k1|s|γ+k2|s|μ)sgn(s) (5) 其中k1>0,k2>0,γ>1,0<μ<1,在上述控制器的控制下,系统(3)的状态轨迹能够达到滑模面上。 =-(k1|s|γ+1+k2|s|μ+1)<0 由Lyapunov稳定性理论,系统状态轨迹滑向滑模面,定理得证。 系统状态轨迹滑向滑模面后,在滑膜面上系统(3)在零点稳定,驱动系统(1)与响应系统(2)是滑模混沌同步的。 利用预估校正算法进行数值仿真。系统参数α=0.35,β=0.1,δ=1.0,f=0.42,ω=1.0,q=0.873时系统呈现混沌态。三种方案设计不同的初始值。 方案一系统初始值设置为:(x1(0),x2(0))=(-1.2,-1.1),(y1(0),y2(0))=(-1.2,-1.5); 方案二系统初始值设置为:(x1(0),x2(0))=(5,3),(y1(0),y2(0))=(3,2); 方案三系统初始值设置为:(x1(0),x2(0))=(0.2,1.0),(y1(0),y2(0))=(1.5,2); 图1 方案一的误差曲线Fig.1 The system errors of case 1 方案一和方案二的误差曲线分别如图1和图2所示;方案三的误差曲线如图3所示,方案三中的滑模面参数取值r=1.5,λ=6,k1=10,k2=4,γ=2,μ=0.5,α=0.873。 从图1-3中可以看出,系统误差在初始时刻较远,随着时间的推移,控制器发挥作用一段时间后,误差渐趋于零,实现系统混沌同步。表明三种方案均是可行的,第一、三两种方案相较于第二种实现同步更加迅速。在我们做出数值仿真的过程中,当控制器不满足方案要求时,偶尔同样可以实现系统同步,这是因为我们所设计的控制方案是充分条件,而非充要条件。 本文研究了一类分数阶Froude混沌系统的同步控制问题,给出了三种同步方案,均可以实现系统同步;并基于Lyapunov稳定性理论,给出控制律设计过程和严格理论证明,理论结果和数值仿真表明,在所构造方案得出的控制器作用下,主从系统是混沌同步的。我们的设计方案有一定的普适性,对于其他混沌系统有很好的借鉴作用。数值仿真表明有效性和可行性。 图2 方案二的误差曲线 Fig.2 The system errors of case 2 图3 方案三的误差曲线 Fig.3 The system errors of case 3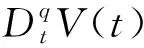
1.3 控制方案三
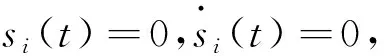

2 数值仿真
3 结 论