☉浙江省杭州市瓶窑中学 叶高娇

众所周知，圆锥曲线是中学数学的重点和难点，在高考中始终占据着重要地位.从学生学习的现状来看，我们不难发现圆锥曲线始终是学生较大的“软肋”.究其原因，笔者认为主要有三：第一，圆锥曲线本身的运算要求更高，而应试中短时间内的高要求，运算则显然是大多数学生较为薄弱的环节；第二，圆锥曲线概念、性质以及综合运用能力弱，这主要是因为复习教学没有合理的整合性，教师合理的整合才能有助于学生合理的掌握；第三，也是最为重要的一点，没有针对近年来高考热点问题、重要问题进行分析、思考和追踪，从高考真题中寻找考查的热点，做到有的放矢，这是复习教学的关键.

自2004年浙江高考自主命题以来，浙江卷对于核心知识的命题出现了不少经典问题.这些经典问题既考查了学生的基本知识和基本技能，也从立足于教材的角度作出了很好的区分，浙江卷给人以亲切而不高冷，区分又非常合理的一种态度.本文结合本省近年来较有代表性的问题与大家一起分享，以便给后续的复习教学一些新的启发、新的思考.

一、定义考查的新视角

定义的考查是高考命题的基本方向，但是定义考查的新意却是比较难实现的.不难发现，以往对圆锥曲线定义的考查主要集中在圆锥曲线的感性定义之中，因此区分度较小，即便考查也没有新的视角，属于简单问题.浙江卷的命题意图却从全新的视角出发，考查圆锥曲线的定义及其相关知识，从显而易见的角度辨别学生是否理解圆锥曲线的含义，可谓从教材出发，高处着眼学生知识体系和能力立意.

例1 （2015年浙江文7）如图1，斜线段AB与平面α所成的角为60°，B为斜足，平面α上的动点P满足∠PAB=30°，则点P的轨迹是（ ）.

（A）直线

（B）抛物线

（C）椭圆

（D）双曲线的一支

图1

分析：本题的载体是空间几何，但是选项是清一色的圆锥曲线，对学生而言，这样的问题显然是知识整合处的考点，那么问题立足于教材哪里呢？以往的教学做了那么多的模拟题，是否认识到这样的问题才是源自教材又高于教材的好题.学生解决这样的灵活考题，往往缺失了知识的联系性，不妨让我们翻开人教版教材选修2-1，来到圆锥曲线一章的第一页，你能看到下列三幅图组成的章头图，如图2.

图2

古希腊数学家在沙滩上研究对顶圆锥时，用不同角度的平面去截圆锥，发现了圆、椭圆、双曲线和抛物线，因此圆锥曲线就此得名.教材中正是以这样的章头图引入，告诫学生其名称的真正含义.令人惋惜的是，笔者发现不少教师在教学时对章头图都没有认真思考过，很多学生到高三毕业都不知道圆锥曲线的真正含义？这样的教学又有多少意义？让我们回头思考原题：先将平面抽离，则动点P满足∠PAB=30°在空间的轨迹是以斜线段AB轴，以AP为母线的圆锥表面，若将平面α垂直于轴AB插入，则显然轨迹是圆；若将平面α与轴AB成30°角插入，则显然轨迹是抛物线；现斜线段AB与平面α所成的角为60°，其轨迹介于抛物线和圆之间，显然是椭圆.将空间几何问题与解析几何问题融合考查，成为浙江高考圆锥曲线问题的新视角.再来看一道浙江的真题.

例2 （2008年浙江理10）如图3，AB是平面α的斜线段，A为斜足，若点P在平面α内运动，使得△ABP的面积为定值，则动点P的轨迹是（ ）.

（A）圆 （B）椭圆

（C）一条直线 （D）两条平行直线

图3

图4

通过对比研究，我们不难发现浙江卷的试题命制总是有“似曾相识燕归来”的感觉，研究高考可以从研究高考试题的共性下手，研究问题背后的数学本质，研究教材中最值得我们教学的知识核心.笔者以为这正是这些概念考查问题带给我们的新思考，引导高三概念复习教学追求回归教材、思考教材、挖掘教材.有兴趣的读者可以进一步研究这些变式问题：

变式1：如图4，AB是平面α外固定的斜线段，B为斜足.若点C在平面α内运动，且∠CAB等于直线AB与平面α所成的角，则动点C的轨迹为_________.（答案：抛物线.）

变式2：二面角α-l-β大小120°，AB垂直平面β交l于B，动点C满足AC与AB成40°角，则点C在平面α和平面β上的轨迹分别是___________.（答案：双曲线、圆.）

二、性质考查的新视角

对于圆锥曲线性质的考查，浙江高考命题也可谓精挑细选，以一种“犹抱琵琶半遮面”的感觉出现.众所周知，椭圆、双曲线、抛物线有非常多的性质，在各种模拟试卷中对其性质的研究不可谓不深，甚至某些性质达到了专家研究的级别，但是高考命题却反其道行之，不以“偏、难、繁”为对象，而是以教材所讲述的基本性质为考点进行编制，再一次体现复习教学以教材为纲，又高于教材的基本要求.笔者以2011年浙江理科填空压轴为例，来思考性质考查的新视角.

例3 （2011年浙江理17）设F1，F2分别为椭圆1的左右焦点，点A，B在椭圆上，若，则点A的坐标是________.

图5

分析：初读本题，感觉试题表述言简意赅，而且定值类问题应该在难度上也不会太大，但是笔者给学生尝试后发现，学生对于问题的理解却是直观的很，其思维方式根本没有立足椭圆的基本性质思考，看一下学生的尝试：设直线AF1的斜率为k（k＞0），则直线AF1的方程为）.联立椭圆x2+3y2=3，得（1+3k2）x2+采用这样的方法处理的学生基本只能停留在此，为什么做不下去了呢？我们发现，学生对于圆锥曲线问题的求解已经被训练成了一种模式化、套路化，即直线和圆锥曲线进行联立，采用韦达定理代入代数条件获得解决，一旦韦达定理失效，则学生慌乱失措.本题恰好是找到了应试教学的软肋！其实学生的方式不是不能做，我们将其解决完毕，结合图5可知，此时xA=0，点A的坐标是（0，1）.同理，当k≤0时，点A的坐标是（0，-1）.但是，这样的运算去处理在一个填空问题上，显然是得不偿失的.那么教师应该思考，高考试题到底考查了学生什么呢？看似平淡无奇，其背后隐藏的数学性质是什么呢？

我们回顾圆锥曲线椭圆第一课，在介绍椭圆性质的时候，我们阐述了椭圆对称性是其最基本的性质，其关于坐标轴和原点对称，既是中心对称图形也是轴对称图形.高考命题正是基于此，从教材视角入手，我们思考本题的解答应该是从对称性入手：如图6所示，设直线AF1与椭圆的另一个交点为B1，设点A的坐标为（x1，y1），点B的坐标为（x，y），由及椭圆对称性可知，

图6

122|F1A|=5|F1B1|，得y1=-5y2.设直线AF1为：x=ty-，联立椭得y1=±1.故点A的坐标是（0，±1）.

本题的合理思路才是命题者想传递的，其以教材椭圆最基本的对称性为出发点，巧妙地将线段利用中心对称作出，形成了学生普遍可以使用的韦达定理，这才是基于教材又高于教材最合理的体现.对于这一经典的高考真题，我们不妨对其进行改编尝试：

改编1：如图7，设F1，F2分别为双曲线x2-y2=1的左，右焦点，点A，B分别在双曲线的左右两支上，且满足，则直线FA的斜率为______.

1

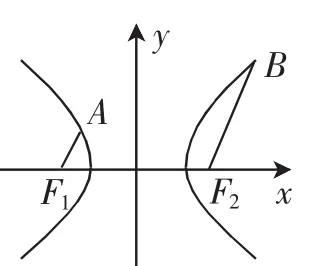
图7

分析：如果理解了例3，自然一眼就看透了本题，双曲线中心对称的性质跃然纸上，利用这一对称性.我们可以将其转换为合理的常态问题解决.笔者认为，对于高考所考查的视角，教师要注重其数学问题背后的知识，要反复体会，要多角度思考，要以不同载体进行训练（.答案：±

改编2：点P为双曲线=1（a＞0，b＞0）第一象限内动点，A1，A2为实轴端点，O为坐标原点，记直线PA1，PO，PA2斜率分别为k1，k2，k3，若0＜k·1k·2k3＜27且可取遍开区间（0，27）内任意实数，则双曲线离心率为_________.

分析：椭圆、双曲线中有不少经典的性质，从深度的角度来说，可能做不到面面俱到，但是常见的性质需要教师提醒复习到位.如椭圆=1（a＞b＞0）长轴顶点与椭圆上动点P（m，n）（不重合于长轴顶点）连线的斜率乘积；双曲线=1（a＞0，b＞0）实轴顶点与双曲线上动点P（m，n）（不重合于实轴顶点）连线的斜率乘积2.本题笔者编制的时候恰以上述性质为背景，有了这样的知识背景，本题的解决自然水到渠成.本题 中，又0＜k1·k2·k3＜27且可取遍开区间（0，27）内任意实数，所以

三、运算考查的新视角

以往的直线和圆锥曲线综合性问题，大量的复杂运算往往是必备的.但是近年来浙江卷却反其道行之，大量运算的圆锥曲线试题并不是考查的首选，而是以非常态运算作为考查的第一准则，即首先讲求算理，有了合理的算理再讲求运算，圆锥曲线问题已经脱离了以往一味的死算、蛮算，进入了拥有合理算理的全新运算视角，教学要以这样的真题作为教学的导向，让学生理解合理的算理，也要让教师明白很多模拟卷上的圆锥曲线综合性问题都是“误人子弟”.

（1） 已知直线l的斜率为k，用a，b，k表示点P的坐标；

图8

（2）若过原点O的直线l1与l垂直，证明：点P到直线l1的距离最大值为a-b.

分析：本题第（1）问实则是椭圆上一点的切线性质，大部分学生无视知识的类比：过圆x2+y2=r2上一点P（m，n）作圆的切线，则切线方程为mx+ny=r2.圆和椭圆实则是同一曲线，自然而然在切线的性质上是异曲同工的.第（2）问实则是函数问题的研究，既可以从函数视角建立模型，也可以寻找不等式的方式，但是显然与模拟试卷中的常态运算完全背离，可见命题者对学生运算处理能力高度上的考查，那些一味靠直线与圆锥曲线联立死算的学生则往往败下阵来.

结合①②及P在第一象限，得

第（2）问：从问题的一般算理角度出发，自然是点到直线的距离公式，这是比较合理的、容易想到的算理.可时有最大值.

当然本题还有不等式的算理，这不过是技巧上的选择：设P（x0，y0）是椭圆=1上一点，且x0＞0，y0＞0，则椭圆在P点处切线l方程为，所以椭圆在P点处法线l2方程为显然题设中的P点到直线l1距离恰等于坐标原点到此法线l2的距离，设该距离为，于是由柯西不等式值为a-b.

从2014年开始，有兴趣的读者可以研究下浙江卷圆锥曲线综合性问题，其思维的难度相比以往有所上升，但是其大量的运算却不见得提升，这与命题者努力提高选拔的思维层次性指导方针密不可分.因此笔者认为教学中研究这些真题对于复习教学是大有裨益的.限于篇幅，本文研究了近年来浙江高考中的新的方向，也限于水平不可能面面俱到，但是从概念、性质、算理的视角来说，高考命题者一直在不断求变，教师要紧紧围绕这些试题所传递的信息，将这一信息从中提炼出来，不断分析、总结，使其在圆锥曲线学习环节获得全新的认知和思考，同时也提升教师自身专业化的素养.

1.石志群.高考数学命题思路分析及复习策略［J］.中学数学月刊，2009（11）.

2.渠东剑.探究方法比探究结果更重要［J］.中学数学教学参考（高中），2013（4）.

3.宋卫东.从生“动”到生动，诠释思维品质的提升［J］.中学数学月刊，2013（5）.

4.朱永祥.再谈数学思想方法的挖掘和应用［J］.中学数学（上），2008（2）.