一类对称双势阱Duffing系统周期解的衍生与演化

2017-12-19肖世富陈红永牛红攀

复杂系统与复杂性科学 2017年3期

关键词：势阱振子非对称

肖世富，陈红永，牛红攀

(中国工程物理研究院总体工程研究所，四川绵阳 621999)

一类对称双势阱Duffing系统周期解的衍生与演化

肖世富，陈红永，牛红攀

(中国工程物理研究院总体工程研究所，四川绵阳 621999)

针对自旋单自由度三次强化弹簧—质量振子系统建立的对称双势阱Duffing方程，通过把数值计算与谐波平衡半解析分析相结合，系统分析了该类Duffing系统在谐波强迫激励下周期解随激励频率变化的衍生与演化现象，获得了不同频段谐波强迫激励下系统周期解的类型、周期解的衍生模式与演化规律。分析结果表明，该类Duffing方程存在平衡点临域局部周期解以及鞍结点分岔衍生的对称、反对称与非对称等多种全局周期解；局部或无对称性的全局周期解直接通过倍周期分岔通向混沌运动；全局对称周期一解和反对称周期三次谐波解首先各自发生对称和反对称破缺，再通过倍周期分岔演化为混沌。研究有助于深化对Duffing方程非线性现象及其演化规律的认识。

Duffing方程；谐波平衡法；周期解；鞍结点分岔；对称性破缺；混沌

0 引言

非线性因素为动力系统带来了一系列线性系统所没有的复杂动力学现象，包括多解、跳越与滞后、极限环、固有频率漂移、次谐波共振、超谐波共振、组合共振、内共振、倍周期分岔、概周期分岔、混沌运动等等。Duffing方程是一类典型的非线性动力系统，是Duffing于1918年描述机械系统中弹簧硬化效应建立的一类方程，具有如下形式

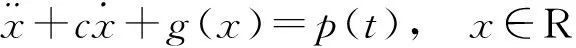
Duffing方程蕴含着丰富的复杂非线性现象，包括周期振动、次谐波共振、局部与全局倍周期分岔、对称与反对称破缺、概周期运动、混沌以及多种周期或混沌运动共存等。因此，在非线性振动理论中研究Duffing方程具有解剖一只麻雀的作用[1]。目前，Duffing方程与van der Pol方程是非线性振动问题研究中最常用的例子[1-3]，在力学、电子学等领域具有广泛的研究和应用价值。

刘延柱等[2]和闻帮椿等[3]系统地总结了求解弱非线性Duffing方程近似解析解的各种方法。Marina和Herisanu[4]给出了求解强非线性Duffing系统近似解析解的积分迭代方法。陈艳锋等[5]对无阻尼Duffing方程自由振动频率的求解方法进行了探讨,应用Gauss*Chebyshev求积公式计算了Duffing方程的自由振动频率,得到了精确解析解表达式。王坤等[6]获得了一类Duffing振子系统具有唯一周期解的必要条件，给出了一定条件下Duffing振子系统精确周期信号的获取方法。冯少东与陈立群[7]利用同伦分析方法求解了恢复力为有理函数的Duffing简谐振子的响应和频率的近似周期解，与精确解吻合。混沌是非线性动力学系统研究的重点之一，倍周期分岔被公认为是通向混沌的道路之一，而在对称非线性系统中，对称破缺又是倍周期分岔的前兆[8-9],驱动振子逃离势阱[10-11]。谐波强迫激励对称Duffing方程存在倍周期分岔演化混沌现象，其对称性破缺研究也获得了学术界的关注。Novak和Frehlich研究表明Duffing系统是由对称破缺到倍周期分岔进入混沌的一个典型例子[8]；毕勤胜等研究了单势阱Duffing方程对称破缺分岔转迁集的解析表达式[9]；张莹等研究了谐波激励双势阱Duffing方程混沌与周期吸引子的对称破缺激变[12]，以及随机参数Duffing系统的对称破缺分叉[13]。

目前，对Duffing方程蕴含的复杂性已经有比较深入的认识，然而，也存在一些认识不够深入的问题。例如Duffing方程的周期解是如何衍生的？其反对称和非对称周期解是如何演化的？本文针对这些问题，以自旋单自由度三次强化弹簧—质量振子系统建立的对称双势阱Duffing方程为例，采用数值计算与谐波平衡半解析分析相结合的方法，系统分析该类Duffing系统在谐波强迫激励下周期解随激励频率变化的衍生与演化现象，进一步提升对Duffing方程非线性复杂现象及其演化规律的认识。

1 双势阱Duffing方程数学模型与周期解

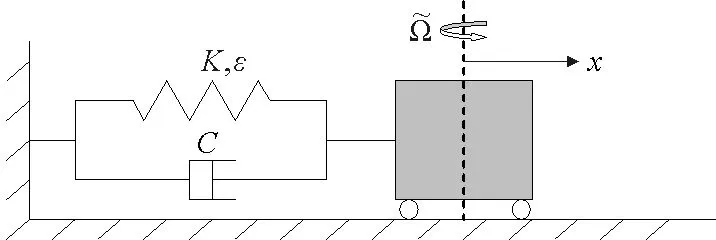
图1 转动单自由度弹簧-质量振子系统示意图Fig.1 Sketch of the rotational single degree of freedom spring-mass oscillator system

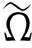
F=Kx+εKx3

(1)

其中，K为弹簧刚度，ε为三次非线性强化系数。

(2)

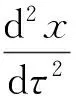
(3)

方程(3)对应的势能为

(4)

其静态平衡解满足

(1-Ω2)x+εx3=0

(5)

当Ω<1时，方程(5)只有稳定的平凡解零解；当Ω≥1时，平凡解发生叉式分岔而失稳，系统存在1对对称稳定的分岔解：

(6)

此情况下，系统的势能函数与准静态分岔图如图2所示。

图2 对称双势阱Duffing方程的势能函数和准静态分岔图Fig.2 Diagram of the potential energy and quasi-static bifurcation solution of the symmetric double-well Duffing equation

当Ω<1时，方程(3)周期解的性质研究已非常成熟，本文不再讨论。对Ω>1于，方程(3)为负刚度强化系统，是一类典型的强迫谐波激励对称双势阱Duffing方程，下面通过数值模拟分析不同频段谐波激励下该系统的周期解。为了分析的方便，确定参数ε=0.3，Ω=1.05，c=0.04，f=0.2，只考查不同激励频率ω下系统的周期响应。

对于方程(3)，在取定的参数下，采用数值计算软件对系统的周期解进行分析，在不同激励频率和初值情况下，系统的周期解如图3所示。

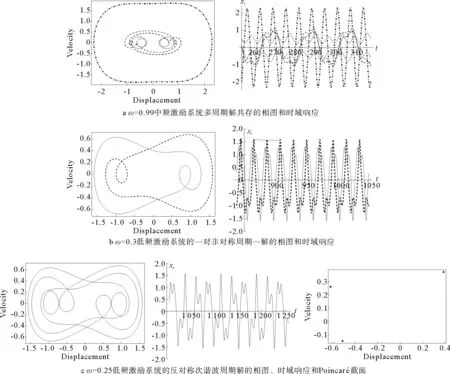
图3 不同频率谐波激励下对称双势阱Duffing系统存在的部分周期解Fig.3 The partial periodic solutions for the symmetric doubkle-well Duffing systems under the harmonic excitation of different frequencies

图3表明，在不同频段谐波激励下，对称双势阱Duffing方程存在多种周期解，包括静态稳定平衡点临域的局部周期解(图3a黑粗线所示)、全局反对称次谐波周期解(图3a虚线所示)、全局对称周期解(图3a幅值最大的周期解)、低频非对称周期解(图3b所示)、低频反对称次谐波周期解(图3c所示)、低频反对称周期解(图3d、图3e所示，表明不仅仅是次谐波是反对称的)，且多种周期解往往共存(图3a所示，非线性动力系统中，还可出现混沌与周期解共存的现象，本文不作分析)。图3a共有5个周期解，包括两个静态平衡点附近的局部二周期解、两个全局三周期次谐波解、以及1个全局大范围的对称一周期解，这些周期解存在各自的吸引域，将使Duffing系统重复正弦扫频实验从本质上出现不同的实验结果。

Duffing系统的这种多周期解共存特性，可解释即使系统本身没有不确定性和再精细的控制，非线性系统振动实验的实验结果也可能不重复现象的内在机理。

2 周期解的衍生

强迫谐波激励对称双势阱Duffing方程的周期解分析表明，系统存在多种周期解，包括全局反对称次谐波解、全局对称周期解、全局非对称周期解等，本文采用谐波平衡法[3]分析这些周期解衍生的分岔模式。

设方程(3)的全局反对称次谐波解具有以下形式

x(τ)=A1cos(ωτ/3)+B1sin(ωτ/3)+A2cosωτ+B2sinωτ

(7)

将表达式(7)代入方程(3)，应用谐波平衡法，得到

(8)

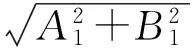
(9.1)

将代数方程(8)的后两式平方求和，并由前两式做变换消去交叉项有

(9.2)

联立代数方程(9.1)、(9.2)进行数值求解，结果表明次谐波由鞍结点分岔衍生，其临界激励频率为ωc=1.33，其衍生的分岔模式如图4所示。

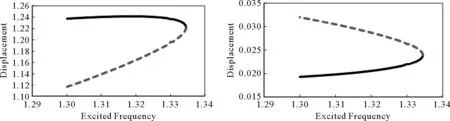
图4 次谐波周期解的衍生模式Fig.4 Derivation pattern of sub-harmonic periodic solution

设方程(3)的全局对称周期解具有以下形式

x(τ)=ρ1sin(ωτ+φ)

(10)

图5 全局对称周期解的衍生模式(ρ1～ω)Fig.5 Derivation pattern of global symmetric periodic solution(ρ1～ω)

将表达式(10)代入方程(3)，将由谐波平衡法得到的两式求平方和有

(11)

代数方程(11)可解析求解，但其表达式非常复杂。仍然采用数值方法，分析表明全局周期解也由鞍结点分岔衍生而成，临界激励频率为ωc=1.07，其衍生模式如图5所示。

设方程(3)全局非对称周期解具有以下形式

x(τ)=A0+ρ1sin(ωτ+φ1)+ρ2sin(2ωτ+φ2)

(12)

将表达式(12)代入方程(3)，应用谐波平衡法，并消去相位变量，有

(13)

数值计算(13)表明，非对称周期解仍然通过鞍结点分岔衍生，其临界激励频率为ωc=0.32，其衍生模式如图6所示。

同理可采用谐波平衡法分析低频激励下系统出现的反对称周期解、反对称次谐波周期解等周期解衍生的模式，分析的关健是谐波需要假设合理的形式。分析结果表明，本文所讨论的强迫谐波激励对称双势阱Duffing方程初期演化的周期解都通过鞍结点分岔衍生而成。

3 周期解的演化

3.1 局部周期解的倍周期分岔

双势阱Duffing方程静平衡位置临域的局部周期解通过倍周期分岔进入混沌，其分岔图如图7a所示，相平面演化如图7b～图7f所示。

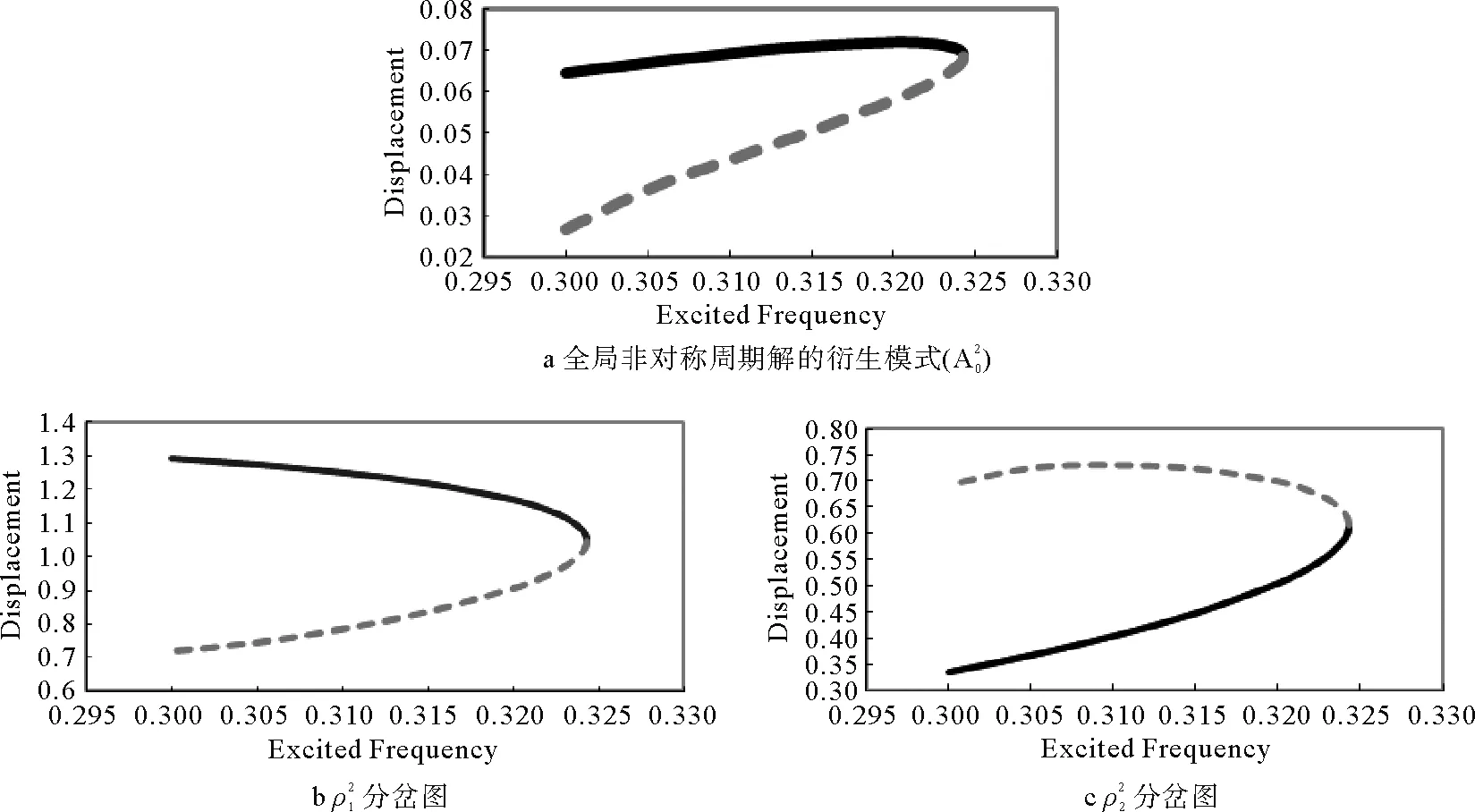
图6 全局非对称周期解的衍生模式Fig.6 Derivation pattern of global asymmetric periodic solution

图7 局部周期解的分岔图与倍周期分岔演化相图Fig.7 Bifurcation diagram and Phase diagram of the evolution of local periodic solution

需要说明的一点是，图7b～图7f周期解演化相图仅给出了系统其中一个平衡点临域局部周期解的相平面演化图，其另一个平衡点临域局部周期解同样通过倍周期分岔进入混沌，且与图7所给的相应结果关于速度轴对称。

3.2 全局反对称次谐波解的对称性破缺与三倍周期分岔

数值分析表明，双势阱Duffing方程由鞍结点分岔衍生的全局次谐波解随着激励频率的下降，相轨迹首先发生反对称破缺，随后以3的倍数发生分岔，演化到概周期直至混沌状态，其分岔图如图8a所示，相轨迹演化如图8b～图8f所示。然而，数值模拟中，次谐波共振周期解三倍周期分岔的概周期与混沌状态比较难于捕捉。

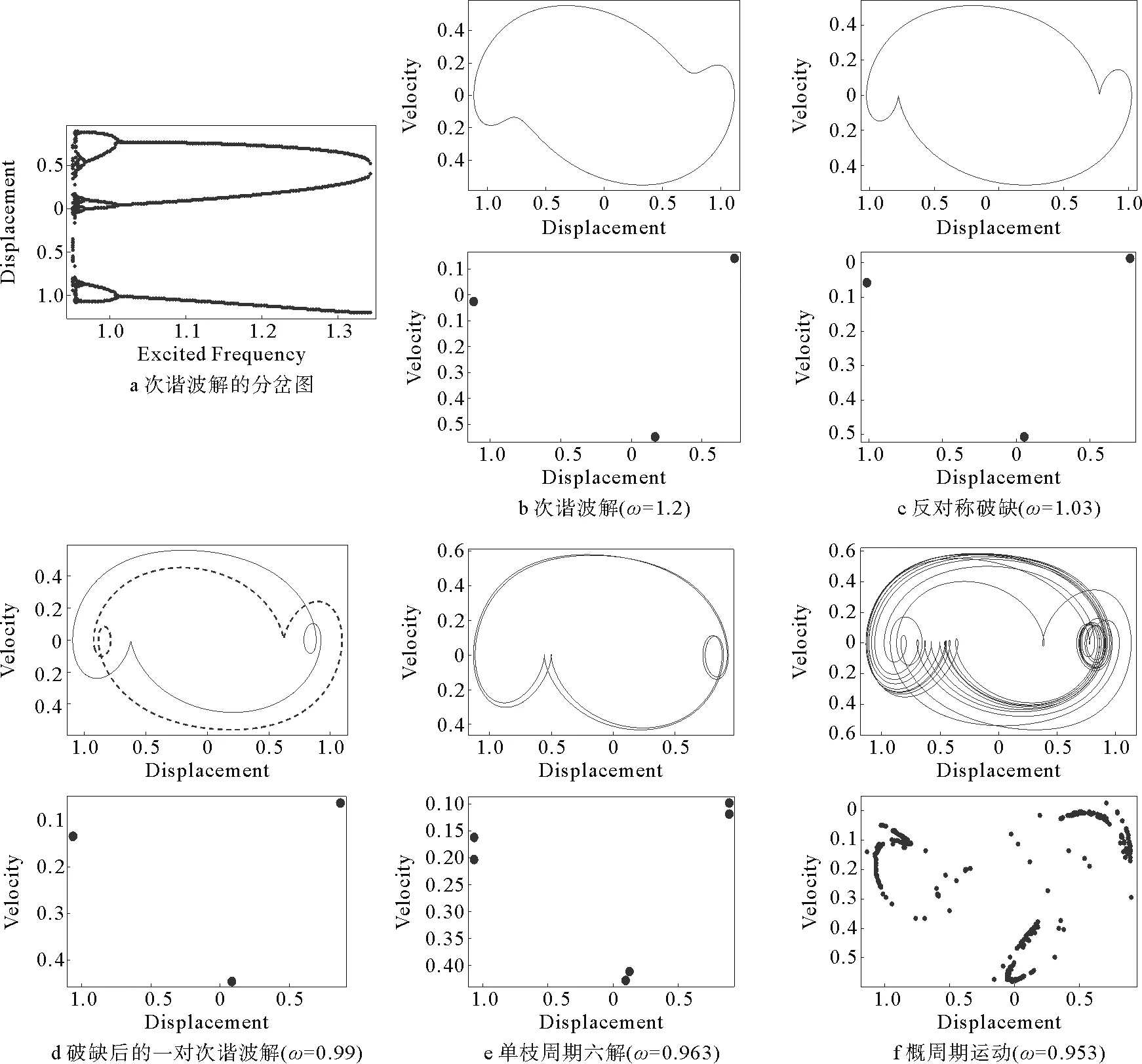
图8 全局次谐波相轨迹的反对称破缺及其分岔现象Fig.8 Anti-symmetry breaking and bifurcation of global subharmonic phase trajectory

图9的分析结果表明，双势阱Duffing方程全局次谐波周期解反对称破缺后，解的周期数并没改变，仅是解的个数加倍，有的文献直接将对称性破缺后的解认为周期加倍是值得商榷的。

4 结束语

本文建立了自旋单自由度三次强化弹簧—质量振子系统的对称双势阱Duffing方程，采用数值计算与谐波平衡半解析分析相结合的方法，系统分析了该类Duffing系统在谐波强迫激励下周期解随激励频率变化的衍生与演化现象，获得以下结果：

1)Duffing方程在不同频段谐波强迫激励下，存在多种周期解：平衡点临域局部周期解、全局对称周期解、全局反对称次谐波周期解、低频全局非对称周期解(成对出现)、低频全局反对称周期解、低频全局反对称次谐波周期解等。

2)Duffing系统周期解由两类模式衍生：静态平衡点临域衍生的局部周期解；鞍结点分岔衍生全局对称周期解、全局反对称次谐波周期解、全局非对称周期解等。

3)Duffing系统平衡点临域衍生的局部周期解直接通过倍周期分岔演化为混沌；鞍结点分岔衍生的全局对称周期一解和反对称周期三次谐波解首先发生对称性破缺(对称/反对称破缺)，再通过倍周期分岔演化为混沌、或通过三倍周期分岔演化为概周期运动。

这些成果有助于深化对Duffing方程非线性现象及其演化规律的认识；同时，也能为实际工程结构振动试验时出现的一些现象和问题提供机理性解释。例如，非线性工程结构振动实验时，经常出现重复实验的实验结果不重复或偶尔出现控制超差等现象或问题，其原因除了研究对象或实验系统的不确定性以外，非线性系统的多解、突变等特性也是重要原因。

[1]丁同仁. 常微分方程定性方法的应用[M]. 北京: 高等教育出版社, 2004.

[2]刘延柱, 陈立群. 非线性振动[M]. 北京: 高等教育出版社, 2003.

[3]闻邦椿, 李以农, 韩清凯. 非线性振动理论中的解析方法及工程应用[M].沈阳: 东北大学出版社, 2001.

[4]Marinca V, Herisanu N. Periodic solutions of Duffing equation with strong nonlinearity[J]. Chaos, Soliton and Fractals, 2008, 37(1): 144-149.

[5]陈艳锋, 郑建华, 吴新跃,等. 无阻尼Duffing方程高精度近似解研究[J]. 机械科学与技术, 2008, 27(12): 1591-1594.

ChenYanfeng, Zheng Jianhua, WuXinyue, et, al. On high-accuracy approximate solution of undamped Duffing equation[J]. Mechanical Science and Technology for Aerospace Engineering,2008, 27(12): 1591-1594.

[6]王坤, 关新平, 丁喜峰,等. Duffing振子系统周期解的唯一性与精确周期信号的获取方法[J]. 物理学报, 2010, 59(10): 6859-6863.

Wang Kun, Guan Xinping Ding Xifeng,et al. Acquisition method of precise periodic signal and uniqueness of periodic solutions of Duffing oscillator system[J]. Acta Physica Sinica, 2010, 59(10): 6859-6863.

[7]冯少东, 陈立群. Duffing简谐振子同伦分析法求解[J]. 应用数学和力学, 2009, 30(9): 1015-1019.

Feng Shaodong, Chen Liqun. Homotopy analysis approach to the Duffing-Harmonic oscillator[J]. Applied Mathematics and Mechanics, 2009, 30(9): 1015-1019.

[8]Novak S, Frehlich R G. Transition to chaos in the duffing oscillator[J]. Physical Review, 1982, 26A: 3660-3663.

[9]毕勤胜, 陈予恕. Duffing系统解的转迁集的解析表达式[J]. 力学学报, 1997, 29(5): 573-581.

Bi Qinsheng, Chen Yushu. Analytical expression of transition boundaries of the solution of Duffing systems[J]. Acta Mechanica Sinica, 1997, 29(5): 573-581.

[10] Bishop S R, Sofroniou A, Shi P. Symmetry-breaking in the response of the parametrically excited pendulum model[J]. Chaos, Solitons and Fractals, 2005, 25(2): 257-264.

[11] Mann B P,Koplow M A. Symmetry breaking bifurcations of a parametrically excited pendulum[J]. Nonlinear Dynamics, 2006, 46(4): 427-437.

[12] 张莹, 雷佑铭, 方同. 混沌吸引子的对称破缺激变[J]. 物理学报, 2009, 58(6): 3879-3805.

Zhang Ying, Lei You-Ming, Fang Tong. Symmetry breaking crisis of chaotic attractors[J]. Acta Physica Sinica, 2009, 58(6): 3879-3805.

[13] Zhang Y, Du L, Yue X L, et al. Analysis of symmetry breaking bifurcation in duffing system with random parameter[J]. Computer Modeling in Engineering & Sciences, 2015, 106(1): 37-51.

PeriodicSolutionsInitiationandEvolvingofaSymmetricalDouble-PotentialWellDuffingSystemwithForcedHarmonicExcitation

XIAO Shifu, CHEN Hongyong, NIU Hongpan

(Institute of Systems Engineering, CAEP, Mianyang 621999, China)

For a Duffing equation with symmetrical double potential well, which is derived from a self-rotating mass-spring pendulum with three-order nonlinear stiffness, the periodic solutions type, initiation mode and evolving behavior adapting to the frequency of excitation are investigated meticulously by Harmonic Balance Method and numerical simulation. Some rewarding results are obtained. This Duffing system has local periodic solutions in the region near its equilibrium point and many global periodic solutions with symmetry, antisymmetry and dissymmetry. The global periodic solutions derive from saddle-node bifurcation. The local periodic solutions and the dissymmetrical global periodic solutions evolve directly into chaos passing through double-periodic bifurcation. The symmetrical global 1-periodic solutions evolve into chaos through passing the double-periodic bifurcation only after losting their symmetry by symmetry-breaking, and the antisymmetric global 3-periodic solutions evolve into quasi-periodic solutions through passing the triple-periodic bifurcation also after lost their symmetry by antisymmetry-breaking.The studies help to raise the understanding of the nonlinear phenomenon and the evolution of solutions of the Duffing equation.

duffing equation; harmonic balance method; periodic solution; saddle-node bifurcation; symmetry-breaking; chaos

1672-3813(2017)03-0103-08；

10.13306/j.1672-3813.2017.03.011