Sliding mode control of engine-variable pump-variable motor drive system①
2017-12-19ZhaoLijun赵立军WangYingWeiYuyingLiuQingheYinChengshun
Zhao Lijun (赵立军), Wang Ying, Wei Yuying, Liu Qinghe, Yin Chengshun
(*School of Automobile Engineering, Harbin Institute of Technology at Weihai, Weihai 264209, P.R.China) (**Shanghai Pal-Fin Automatic Control Technology Co., Ltd, Shanghai 201206, P.R.China)
Sliding mode control of engine-variable pump-variable motor drive system①
Zhao Lijun (赵立军)*, Wang Ying②, Wei Yuying*, Liu Qinghe*, Yin Chengshun**
(*School of Automobile Engineering, Harbin Institute of Technology at Weihai, Weihai 264209, P.R.China) (**Shanghai Pal-Fin Automatic Control Technology Co., Ltd, Shanghai 201206, P.R.China)
Engine-variable pump-variable motor drive system is a complex nonlinear system. In order to improve system response speed and stability, a sliding-mode variable-structure control based on a feedback linearization theory is analyzed in this research. A standardized system model is established and linearized by the feedback linearization theory, and the input dimension is reduced through the relationship between variables which has simplified the linearization process. Then the sliding-mode controller using an exponential reaching law is designed and the Lyapunov stability of this algorithm is verified. The simulation results show that the sliding-mode variable-structure controller based on the feedback linearization theory can improve system response speed, reduce overshoot and achieve stronger robustness, so the vehicle speed control requirements can be satisfied well.
feedback linearization, sliding mode control, exponential approach law, robustness
0 Introduction
The hydraulic driving system has been widely used in the area of the loading machinery, due to the advantages of convenient arrangements and high power density. The technique has been improved rapidly[1,2], especially in recent years. However, for the engine-variable pump-variable motor drive system, most of researches have been focusing on the control of single or bivariate variables. Even for the bivariate variables system, it is the variety of the single variable drive system. As for the bivariate variables control system in which the variable motor is controlled by the variable pump, it is equal to the method that the variable pump controls the constant motor or the constant pump controls the variable pump[3,4]. In the process of the flow controlling, only one regulating mechanism works, which leads to great loss of excess flow and low speed of the system. The advantages of the system, such as the fast response and the strong ability with load are limited.
The engine-variable pump-variable motor drive system is a three inputs single output nonlinear system. There have been many researches aiming at the nonlinear system both at home and abroad: The Takagi-Seguno (T-S) fuzzy model is adopted by Golea and Schulte[5-7]to estimate the state of system and the dynamic changes, which can achieve asymptotic tracking of the reference model and the estimation of asymptotically stable state. But the parameters’ convergence speed is slow and the results are not ideal. For the parameters’ uncertainty and disturbance of MIMO system, Cai[8]carried out tracking control and proposed a continuous robust adaptive controller based on adaptive control law and dynamic robust control mechanism. For a class of nonlinear MIMO systems, Li[9]proposed the hybrid indirect and direct adaptive fuzzy output tracking control and designed H-infinity control and variable structure control to suppress the influence of the external disturbance and eliminate the fuzzy approximation error; Chang[10]also made comprehensive use of the nonlinear H-infinity tracking control algorithm, a variable structure method and the adaptive control technology to construct a hybrid adaptive robust H-infinity tracking controller, which can be applied to a wider range of class of nonlinear MIMO system with highly uncertain factors.
In view of the research above, this article chooses the needs of response speed and anti-interference ability of the vehicle as the start point, which aims at improving the system’s response speed and stability. The feedback linearization of differential geometry theories helping build the sliding-mode variable structure controller is applied for the research.
1 System model
1.1 Model’s construction
The tandem engine-variable pump-variable motor drive system is chosen as the study object. The configuration of the system is shown in Fig.1.

1-engine 2-variable pump 3- slippage pump 4-oil filter 5- fuel tank 6- overflow valve 7、8- check valve 9、10- safety valve 11-variable motor 12-clutch 13- main reducing gear 14- hub reduction gear
Fig.1 Configuration of the drive system
The overall model which has been established in Ref.[11] is chosen as the research foundation of the sliding- mode control rate. An electric proportional displacement control method is adopted to control the variable pump and variable motor. For convenient calculation, the displacement control model can be simplified as follows:
(1)
where Vpand Vmare the displacements of the variable pump and motor respectively(m3), Vmmaxand Vmkare the maximum and controlled displacement of motor(m3), tpand tmare the time constant(s), kpand kmare the proportionality coefficient(m3/(rad·mA)), and ipand imare the controlled electric current(mA).
Taking the leakage of the motor into account, the flow continuity equation of variable pump and variable motor, and the torque balance equation of variable motor are as follows:
(2)
(3)
where p is the system pressure(MPa), Ctpand Ctmare the total leakage coefficient of pump and motor(m5/(N·s), βeis the hydraulic oil elastic modulus(Pa); ωpand ωmare the rotational speed of the pump and motor(rad/s), V0is the total volume of high pressure chamber of the variable pump(m3), Jmis the rotational inertia of vehicle(kg·m2), Cvis the damping coefficient(N·m/(rad/s)) and TLis the load torque(N·m).
Combining the above three equations, following equation is got:
(4)
1.2 Model standardization
Taking the state variables: x1=Vp, x2=Vmk, x3=p, x4=ωm, Eq. (4) can be simplified as follows:
(5)

From the above equation, it can be seen that both the third and the fourth equations contain multiplied items of state variables, which is the essential nonlinearity. Besides, it is a three inputs (ip, im, ωp)-single output ( ωm) system.
Eq. (5) can be written as follows for the following convenient calculation:
(6)
2 Feedback linearization
2.1 Feedback linearization design theory
The feedback linearization (mainly focusing on the feedback linearization method based on the differential geometry theory) is a method that transforms coordinate appropriately and back feeds the state of system to realize exact linearization of state or input/output, by which the complex nonlinear problem can be converted into comprehensive problem of a linear system. It is a kind of global linearization method, which can not only simplify the design of controller, but also help the controller to ensure the global stability[12,13]. The research is carried based on the single input-single output system to pave the way for the system which is studied in this paper. As for the following single input-single output system[14,15]is got:
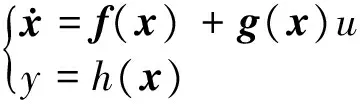
(7)
where, x∈Rnis the state victor, u∈R1is the input of the system, y∈R1is the output of the system.
Calculating the derivative of y: if u(input) does not appear before the γ-1 time derivation but appears at the γ time, and the higher order derivative of u appears with the increasing of the derivation order, then γ is the relative degree of system. It represents the number of the integrator. That is
(8)
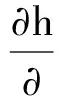
If γ=n, then the precise feedback linearization of the system can be realized. In this case, the appropriate coordinate transformation z=Φ(x) is chosen to convert the system to the form of the following integrator in series:

(9)


The feedback linearization control input of the original system is as follows:

(10)
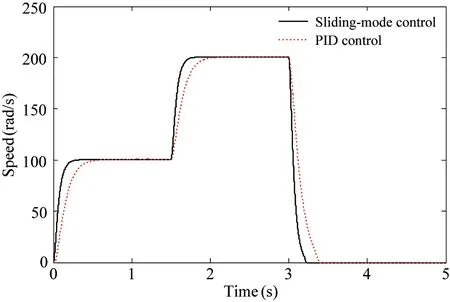
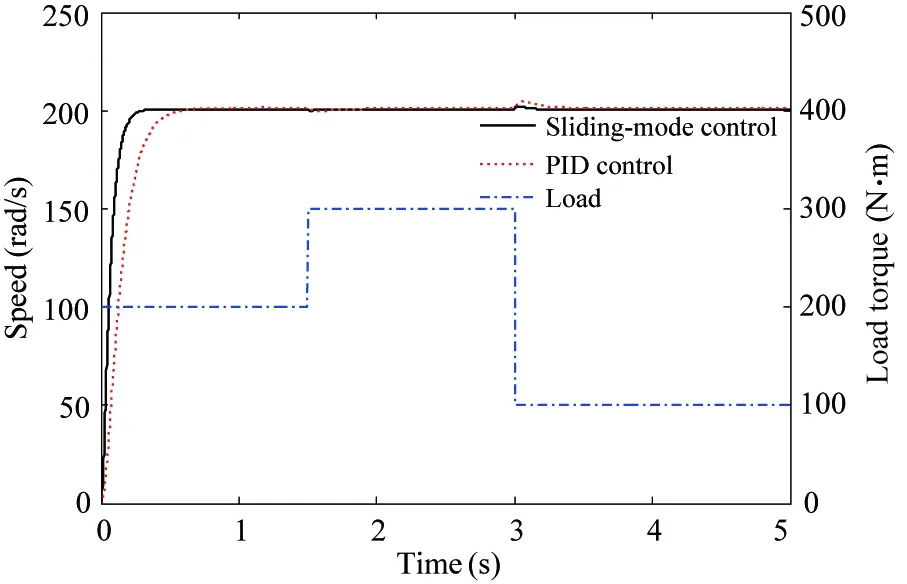
If γ (11) Calculating the derivative of the output y=x4=h(x) to look for the relative degree of the system: (12) =-a8x3f2(x)+(a7-a8x2)f3(x)-a9f4(x)-a8b2x3im=F(x)+G(x)im (13) The relative degree of system: γ=2 (14) The output of the system is (15) (16) The best working speed of engine mapped by the power can be got while the dynamic process of engine is not considered that the engine desired through the control relationship between engine and variable pump introduced in Ref. [11]. And the power that the engine desired is determined by the load. The best speed is chosen as the input of engine to achieve the match between the engine and the load. Sliding-mode variable structure control is essentially a kind of special nonlinear control method. The response time is short and it is not sensitive to parameter variations and disturbance because of its unfixed system structure. Considering the vehicle operation requirements of response speed and anti-interference ability, this paper selects the sliding mode variable structure control algorithm for control system. Also, the chattering problem aroused by the sliding mode control switch characteristics are weakened due to the compressibility of oil and damping effects caused by the hydraulic pipeline’s elastic. First, the switch function is chosen to ensure that the dynamic sliding mode can be stable asymptotically and has good dynamic quality: (17) Calculating the derivative of the Eq. (17), the following is got: (18) In order to restrain the approach trajectory of movement point in state space and weaken the chattering of sliding mode surface, Gao put forward the concept of reaching law. In this paper, a sliding mode controller is designed using the exponential reaching law. For the moving point in the index approach, approximating the switching surface is a progressive process, so it is difficult to ensure the point reaching in time. In order to ensure the reaching speed not zero but ε when s is zero, which can help it reach the destination in limited time, a constant reaching item should be added, which is shown as follows: (19) where, sgn(·)is the signal function,ε>0,q>0. According to Eqs (18) and (19), the sliding-mode controller is deduced: (20) The constructed Lyapunov function is shown as follows: (21) Calculating the derivative of the Eq.(21) and combining Eq.(19), it has: =s(-εsgns(t)-qs(t)) =-εs-qs2<0 (22) Take one 2t load of wheel loader for the parameter matching platform (the vehicle’s basic parameters are shown in Table 1), the selected motor with reduction ratio can meet the loader torque requirements in limited conditions. The drive system simulation is carried out with the help of Matlab/Simulink. The response time of oil pump and hydraulic valve are ignored in the process of the simulation. The simulation parameters are as follows: c1=20, c2=1, ε=30, q=50. Table 1 Basic parameters of the whole vehicle PID control is a common method in the classical control theory. The method and theory are simple and easy to be implemented. The mainstream position is still occupied by the PID control method in the engineering application, as well as all kinds of mechanical control. In theory, the sliding-mode variable structure controller designed in this paper is better than PID controller with its fast response speed and anti-interference ability, which can ensure that the system recovers a stable state with the parameter perturbation and external disturbance. The sliding-mode controller is more applicable for the time-varying load and the complex road conditions in terms of the engineering vehicles. In the following part, the control effect of the sliding-mode controller and conventional PID controller will be compared by simulation and analysis. The critical ratio method is adopted for the PID controller’s parameter setting. When the load is 300 N·m, the sliding-mode variable structure control method is adopted to analyze the expected speed of different motors and the speed saltation. Compared with traditional PID control method, the system response speed can be got, as shown in Fig.2 and Fig.3. From Fig.2 it can be seen that, with the control of the sliding-mode variable structure: when the motor speed is 100 rad/s, the regulating time of system is 0.305s and the overshoot is 0.39%; When the expect motor speed is 200rad/s, the regulating time of system is 0.306s and the overshoot is 0.42%, which indicates that the proposed design of variable structure control in this paper is a good implementation of variable pump controlling the variable motor and expected motor speed tracking. And they have basically the same performance. Besides, the control method keeps the same performance for different speeds, which means that the controller has stronger robustness for different motor speed. Fig.2 System response under different expect motor speed Fig.3 System response under expect motor speed saltation Compared with the traditional PID control method, the response and the adjust time of the system speed up 47.31% and 47.51%, and the overshoot amount of the system is reduced by 54.65% and 44.74%, which indicates that the sliding mode controller can improve the system response speed, reduce the overshoot of the system and realize the desired results. As can be seen from Fig.3, when the system running to 1.5s, the motor’s speed increases suddenly to 200rad/s, the speed of the sliding mode variable structure control restores stability within 0.24s. But the speed under the PID control restores stability after 0.52s; when the system running to 3s, the motor’s speed drops suddenly to 0rad/s, the speed of the sliding mode variable structure control restores stability within 0.25s. However, the speed under the PID control method restores stability after 0.528; the results show that: compared with PID control, the sliding mode variable structure control system has stronger anti-jamming ability, it can help the system recover to a stable state quickly under disturbances. When the motor expected speed is 200 rad/s, simulation and analysis of the load saltation are carried out. Set that: when the system running to 1.5s, load torque increases from 200N·m to 300N·m, then drops to 100N·m at the time of 3s. The results are shown in Fig.4. (a) System response under load saltation (b) Enlarged drawing of system response under load saltation at 1.5s (c) Enlarged drawing of system response under load saltation at 3.0 s Fig.4 System response under load saltation As can be seen from Fig. 4 (a), speed of system converges to the expected speed within 0.307s under the sliding-mode variable structure control, which is faster than PID controller. What’s more, obvious speed fluctuation does not appear with the variable load condition after converging to the expected speed. From Fig. 4 (b) and (c), put it in perspection, when the system running to 1.5s, the motor’s speed suddenly increases from 200N·m to 300rad/s, the speed of the sliding mode variable structure control restores stability within 0.22s. But the speed under the PID control restore stability after 0.48s; when the system running to 3s, the motor’s speed drops suddenly to 100N·m, the speed of the sliding-mode variable structure control restores stability within 0.24s. However, the speed under the PID control restores stability after 0.65s. Besides, the speed has relatively large fluctuations under the PID control system when the load changes suddenly, which means that the sliding mode controller is more sensitive to disturbance caused by error signal, and it can inhibit the speed fluctuation caused by load mutation well. The results of the analysis above show that both two control methods can achieve variable pump’s control to variable motor, as well as tracking the expected motor speed. But from the overall point of view, the sliding mode variable structure control method is obviously better than that of PID control in terms of response time and resistance to disturbance, and the former has strong robust performance under variable load conditions. In order to observe tracking effect of vehicle running speed and the performance of the controller in load mutation cases of the sliding-mode controller designed in this chapter, typical condition of acceleration and deceleration is selected to carry out the simulation. The simulation conditions and the load are shown in Fig.5. System response results are shown in Fig.6 and Fig.7, respectively. From the system status presented in Fig.5~Fig.7, it can be seen that: when the load increases, the hydraulic system pressure increases, too. The motor displacement will be increased to maintain the system pressure, namely the motor speed will be reduced, and the variable pump’s displacement will be increased to adapt to the changes of the status of the motor. The speed of engine will also increase to output more power to adapt to the vehicle load operation requirements; when the load decreases, the pressure of the hydraulic system is reduced, and the motor’s displacement will be reduced with the speed increases. The displacement of the variable pump and the engine speed will be reduced to adapt to the demand of vehicle under low load, which shows that the controller can realize the supply and demand relations between vehicle and load. The working conditions and the system response results are as follows. Besides, the tracking effect of the expected motor speed is pretty well from Fig.7. The tracking error is controlled within ±3rad/s. Put it in perspective, Fig.5 Simulation condition and motor load Fig.6 Simulation results of system states Fig.7(b) shows the system response when the vehicle is starting. The response time can be controlled within 0.5s, and the system has good tracking effect after 0.5s. Fig.7(c) shows the system response when the vehicle running from even speed to accelerating condition. The vehicle restores stable state after 0.3s fluctuations. Fig.7(d) shows the system response when the vehicle running from accelerating condition to even speed. The vehicle restores stable state after 0.2s fluctuations. Fig.7(e) shows the system response when the vehicle starts decelerating. The vehicle restores stable state after 0.2s fluctuations. Considering all the above system response of various circumstances comprehensively, it is concluded that: the design of sliding-mode variable structure controller based on the feedback linearization theory in this paper has the advantages of fast response speed and small steady-state error. And the vehicle running speedcontrol performance can also be satisfied well. Fig.7 Motor speed tracking results and tracking errors (1) Based on the nonlinear engine-variable pump-variable motor drive system, the system is linearized by the feedback linearization theory. And the sliding-mode variable structure controller is designed based on the exponential reaching law. Besides, the Lyapunov stability of the system has been proved critically. (2) Simulation results show that the sliding-mode variable structure controller based on the feedback linearization theory can improve the response speed, reduce system overshoot and it has stronger robustness compared with PID controller. And the vehicle running speed control performance can also be satisfied well. [ 1] Rydberg K E. Hydrostatic drives in heavy mobile machinery-new concepts and development trends. Sae Technical Paper 981989, 1998. doi: https://doi.org/10.4271/981989 [ 2] Hong I T, Fitch E C. Hydraulic system modeling and simulation-compendiums and prospects. In: Proceeding of the 4th International Symposium on Fluid Power Transmission and Control, Wuhan, China, 2003. 30-137 [ 3] Yan W. Modeling and control for variable-pump controlling variable-motor. Control Theory & Applications, 2012, 29(1): 007 [ 4] Ma P F. Dynamics Research of Full Hydraulic Bulldozer Drive System: [Ph.D dissertation]. Xi’an: School of Construction Machinery, Chang’an University,2006. 44-62 (In Chinese) [ 5] Golea N, Golea A, Benmahammed K. Stable indirect fuzzy adaptive control. Fuzzy Sets & Systems, 2003, 137(3):353-366 [ 6] Schulte H. LMI-based observer design on a power-split continuously variable transmission for off-road vehicles. In: Proceedings of the IEEE International Conference on Control Applications, Yokohama, Japan, 2010. 713-718 [ 7] Schulte H, Gerland P. Observer design using T-S fuzzy systems for pressure estimation in hydrostatic transmissions. In: Proceedings of the International Conference on Intelligent Systems Design and Applications, Pisa, Italy, 2009. 779-784 [ 8] Cai Z, De Queiroz M S, Dawson D M. Robust adaptive asymptotic tracking of nonlinear systems with additive disturbance. IEEE Transactions on Automatic Control, 2006, 51(3):524-529 [ 9] Li H X, Tong S. A hybrid adaptive fuzzy control for a class of nonlinear MIMO systems. IEEE Transactions on Fuzzy Systems, 2003, 11(1):24-34 [10] Chang Y C. An adaptive H∞ tracking control for a class of nonlinear multiple-input multiple-output (MIMO) systems. IEEE Transactions on Automatic Control, 2001, 46(9):1432-1437 [11] Zhao L J, Wei Y Y, Liu Q H, et al. Hierarchical control of engine-variable pump-variable motor drive system. Journal of Beijing University of Aeronautics and Astronautics, 2015, 41(8): 1416-1421 (In Chinese) [12] Le J Y, Xie. Sliding-mode variable-structure control of CCM buck converter based on exact feedback linearization. Journal of South China University of Technology, 2012, 40(2): 130-135, 160 (In Chinese) [13] Abbas H A, Belkheiri M, Zegnini B. Feedback linearization control for highly uncertain nonlinear systems augmented by single-hidden-layer neural networks. Journal of Engineering Science & Technology Review, 2015, 8(2):215-224 (In Chinese) [14] Belkhiri M, Ait Abbas H, Zegnini B. Feedback linearization control of nonlinear uncertain systems using single hidden layer neural networks.In: Proceedings of the 11th IEEE International Multi-Conference on Systems, Signals & Devices, Barcelona, Spain, 2014. 1-6 [15] Wang L. Feedback-linearization control of direct-driven permanent magnet synchronous generator wind turbines. Transactions of China Electrotechnical Society, 2011, 26(7): 1-6, 20 10.3772/j.issn.1006-6748.2017.04.003 ①Supported by the National Natural Science Foundation of China (No. 51275126) and the China Aerospace Science and Technology Corporation-Harbin Institute of Technology Joint Technical Innovation Center Fund Project(CASC-HIT15-1A04). ②To whom correspondence should be addressed. E-mail: 2324013645@qq.com on Oct. 14, 2016* his Ph.D degree in Automotive Engineering in Harbin Institute of Technology in 2011. He also received his B.E and M.E. degrees from Harbin Institute of Technology in 1997 and 2003 respectively. His research interests include the technology of special vehicle and new energy vehicle technology.
2.2 Feedback linearization of the system



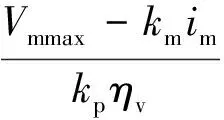
3 Design of variable structure control algorithm
3.1 Switch function and reaching law design



3.2 Stability validation of controller



4 Simulation and results analysis

4.1 Simulation and analysis of sliding-mode controller’s effect

4.2 Simulation and analysis of load robustness


4.3 Simulation and analysis of the vehicle running state



5 Conclusions
杂志排行
High Technology Letters的其它文章
- Temperature field analysis of two rotating and squeezing steel-rubber rollers①
- Operation of the main steam inlet and outlet interface pipe of a nuclear power station①
- Studies on China graphene research based on the analysis of National Science and Technology Reports①
- First order sensitivity analysis of magnetorheological fluid damper based on the output damping force①
- Research on a toolpath generation method of NC milling based on space-filling curve①
- Novel differential evolution algorithm with spatial evolution rules①
