刘 新

（四川信息职业技术学院 基础教育部， 四川 广元 628017）

非奇异M-矩阵及其逆矩阵Hadamard积最小特征值的新估计

刘 新

（四川信息职业技术学院 基础教育部， 四川 广元 628017）

设A是非奇异矩阵，利用圆盘定理和逆矩阵元素的估计式，给出AοA-1的最小特征值的一些新下界估计式.通过理论分析与数值算例，说明新估计式改进了现有的一些结果.

矩阵； Hadamard积； 最小特征值； 圆盘定理

1 引言

2 预备知识

定义1[1,2]设则矩阵A可表示为A=λI-Q，其中Q≥0, 当λ≥ρ（Q）时，则称A为M_矩阵.

定 义2[1,2]设∈Mn，A0.B表示为A和B的对应元素作乘积得到的n阶方阵，即而 A0.B称为矩阵A与矩阵B的Hadamard积 .

定义3[1,2]设那么矩阵A的最小特征值可记为(其中σ(A)表示A的谱).

关 于 τ（AοA-1） 的 研 究，Fiedler和Markham首先在文献[2]中得出结论：若A和B

2007年，李厚彪等[3]改进了上述结果，得出：

李耀堂等人[4]改进李厚彪等人的结论，得到如下估计结果：

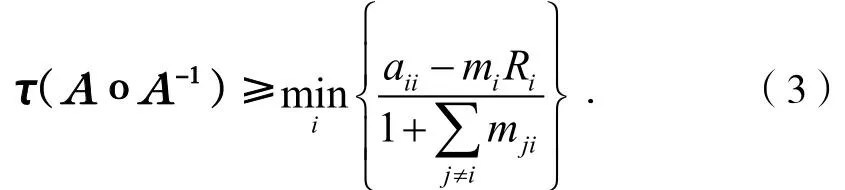
2011年，李耀堂，刘新等人[5]又改进了上述结果：

2013年，杨晓英等人在文献[6]中给出了如下一个估计式：

2012年，文献[7]中得出如下结论：

3、记号与引理

我们先给出一些记号,记[2-6]:

引理1[5]设A=（aij）∈Mn是行严格对角占优M矩阵， A-1=（βij），则

引理2[5]设A=（aij）∈Mn是行严格对角占优M矩阵, A-1=（βij）是双随机矩阵， 则

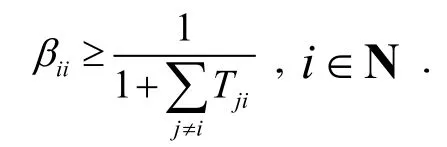
引理 3[8]设为正实数，则矩阵A的所有特征值都位于下列范围之中

4 、τ（AοA-1）的估计

定理1 设A=（aij）∈Mn是不可约M矩阵,是双随机矩阵，则

证明: 由于A-1是双随机矩阵, 由文献[4，定理3.2]可知，0＜mj≤1，i∈N.

令 λ=τ（AοA-1）, 由 引 理3知, 存 在i0（1 ≤ i0≤ n）, 使得

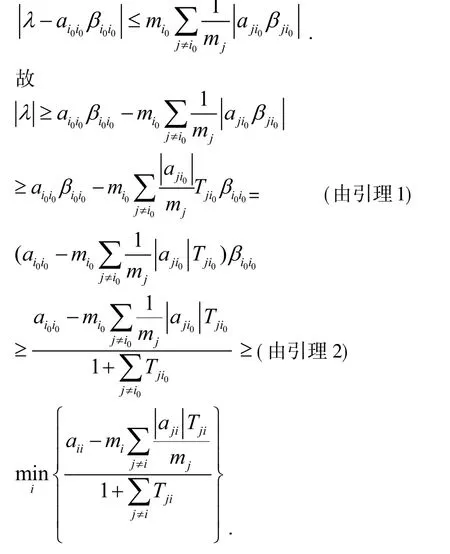
注：若A是可约矩阵，记G=（gij）为 n×n阶置换矩阵，其中其余元素都为零.对于足够小的正数ε，矩阵A-εG的所有顺序主子式均为正.所以当ε＞0足够小时，A-εG就是不可约M矩阵.用A-εG代替A，再令ε→0，则由连续性知结论仍然成立.

定理2 设A=（aij）∈ Mn为 M矩阵, A-1=（βij）为双随机矩阵，则

且

证明: 由文献[5]中定理3.6的证明过程，可知

注: 由定理2的结论可知，定理1的结果优于（3）式和（5）式.

由文献[3，定理2.3]，文献[1，定理4.6.5]和定理1，可得如下结果

5 算例分析

本例子引自文献[3-6]，设

下面利用已有的估计式和本文的结论对τ（AοA-1）进行估计运算：

由本文定理1得：τ（AοA-1）≥0.9262；

事实上，τ（AοA-1）≥.09756.

由上述估计结果知, 定理1很好地改进了文献[2-7]的结果.

[1]陈景良, 陈向晖.特殊矩阵[M].北京：清华大学出版社, 2000: 276-278, 296, 440-441.

[2]Fiedler M, Markham T.An inequality for the Hadamard product of an M-matrix and inverse M-matrix[J].Linear Algebra and Applications, 1988, 101(3): 1-8.

[3]Li Houbiao, Huang Tingzhu, Shen Shuqian, et al.Lower bounds for the minimum eigenvalue of Hadamard product of an M-matrix and its inverse[J].Linear Algebra and Applications, 2007, 420(1): 235-247.

[4]Li Yaotang, Chen Fubin, Wang Defeng.New lower bounds on eigenvalue of the Hadamard product of an M-matrix and its inverse[J].LinearAlgebra and Applications, 2009, 430(4):1423-1431.

[5]Li Yaotang, Liu Xin, Yang Xiaoying et al.Some new lower bounds for the minimum eigenvalue of the Hadamard product of an M-matrix and its inverse[J].Electronic Journal of Linear Algebra, 2011, 22(6): 630-643.

[6]杨晓英, 韩惠丽, 刘新.M-矩阵与其逆矩阵的Hadamard积最小特征值下界的估计[J].西南大学学报(自然科学版), 2013,35(6): 34-38.

[7]刘新, 杨晓英.M-矩阵与其逆矩阵的Hadamard积最小特征值的新下界[J].四川理工学院学报(自然科学版), 2012,25(2): 84-87.

[8]Vargar S.Minimal Gerschgorin sets[J].Pacific Journal of Mathematics, 1965, 15(2): 719-729.

[9]赵建兴，桑彩丽.非奇异M-矩阵的Hadamard积的最小特征值的下界序列[J].西南师范大学学报(自然科学版), 2016,41(8): 1-5.

New Estimate for the Smallest Eigenvalue of Hadamard Product of Nonsingular M-matrices

LIU Xin

( Department of Basic Education, Sichuan Information Technology College, Guangyuan 628017, China )

If A is a nonsingular M-matrix.Some new lower bounds for the minimum eigenvalue of AοA-1are given by using Disk theorem and estimation formula for the elements of inverse matrix.Theoretical analysis and numerical example show that the new bounds improve several results in the literature.

M-matrix; Hadamard product; minimum eigenvalue; Disk theorem

O151.21

A

2095-7408（2017）05-0006-03

2017-07-10

四川省教育厅自然科学基金项目(NO.15ZB0465).

刘新(1983— )，男，山东济宁人，讲师，硕士，主要从事矩阵理论与应用研究.