湖北省广水市第一高级中学432700 聂文喜

对一道高考题的探究

湖北省广水市第一高级中学432700 聂文喜

1.问题再现

题1(2017年高考全国卷III理21)已知函数f(x)=x-1-alnx.

(1)若f(x)≥0恒成立,求a的值;

(2)设m为整数,且对于任意的正整数求m的最小值.

本题以函数与不等式为载体,以不等式恒成立及数列不等式证明为切入点,主要考查学生数学基本知识、数学方法、数学思想的掌握情况,考查分析问题和解决问题的综合能力.本题入口较宽,解法多样,由于不同程度的学生可以根据自已的实际情况,灵活选择问题的解决方法,而思维量的多少,方法的繁简,运算量的大小等方面的因素又引发解题时间的差异及结果的正确与否,因此,它有相当好的区分度,可以很好地甄别出考生能力的差异,从而达到精确区分考生的目的.本文尝试从不同视角寻求突破.

2.解法探究

解法1(视角1f(x)≥0恒成立等价于f(x)min≥0.)

①当a≤0时,对所有的x＞0,f′(x)＞0,所以f(x)在(0,+∞)单调递增,又f(1)=0,所以当0＜x＜1时,f(x)＜0,不符合题意,舍去.

②当a＞0时,令f′(x)＜0,得0＜x＜a,所以f(x)在单调递减,令f′(x)＞0得x＞a,所以f(x)在(a,+∞)单调递增,所以f(x)min=f(a)=a-1-alna,于是对一切x＞0,f(x)≥0恒成立,当且仅当

令g(t)=t-1-lnt,易见,当t=1时,g(t)取得最大值g(1)=0,当且仅当a=1,①成立.综上所述,a=1.

解法2(视角2利用函数最值定义)易发现f(1)=0,所以f(x)≥0恒成立等价于f(x)的最小值为f(1),

①当a≤0时,类似解法1的讨论得到矛盾,不符合题意.

②当a＞0时,令f′(x)＜0,得0＜x＜a,所以f(x)在单调递减,令f′(x)＞0得x＞a,所以f(x)在(a,+∞)单调递增,所以f(x)min=f(a),又f(x)的最小值为f(1),所以a=1.

解法3(视角3分离参数法)f(x)=x-1-alnx≥0⇔alnx≤x-1,

①当0＜x＜1时,x＜1),则,令x＜1),则在(0,1)单调递减,又h(1)=0,所以0＜x＜1,h(x)＞0,从而g′(x)＞0,g(x)在(0,1)单调递增.所以g(x)在(0,1)上没有最大值,且g(1)没有意义,我们考察极限值

解法4(视角4数形结合法)f(x)=x-1-alnx≥0⇔alnx≤x-1,

令f1(x)=alnx,f2(x)=x-1,则问题等价于在区间(0,+∞)上,对数函数的图象恒在一次函数的图象下方.如图1,当直线y=ax与曲线y=ln(x+1)相切时(切点为(

图1

点评f(x,a)＞g(x,a)对x∈A恒成立⇔函数y1=f(x,a)的图像恒在函数y=g(x,a)的上方.

解法 5(视角 5先充分条件再必要条件)易发现,f(1)=0,我们自然想到,若函数f(x)在(0,1)单调递减,在(1,+∞)单调递增,那么f(x)≥0一定成立;

若函数f(x)在(0,1)单调递减,则即可,分离参数得a≥x对0＜x＜1恒成立,所以a≥1;

若函数f(x)在(1,+∞)单调递增,则即可,分离参数得a≤x对x≥1恒成立,所以a≤1;所以a=1.

下面只须说明a/=0时,f(x)≥0不恒成立.当a/=0时,f(a)=a-1-alna,令g(t)=t-1-lnt,t/=1,则g′(t)=-lnt,所以g(t)在(0,1)单调递增,在(1,+∞)单调递减,g(t)＜g(1)=0,故当a/=1时,f(a)＜0,不符合题意.综上,a=1.

点评 因为f(1)=0,所以函数f(x)在(0,1)单调递减,在(1,+∞)单调递增是f(x)≥0的充分条件,解法5先利用充分条件求出参数a的值,再证明所求的值满足必要性.

解法6(思路 6先必要条件再充分条件)f(x)=x-1-alnx≥0⇔alnx≤x-1,

所以a≥1.②当x＞1时,所以

所以a≤1.故a=1.

下面只须证明当a=1时,不等式a(x-1)≥lnx成立,只须证明x-1≥lnx,只须证明lnx-x+1≤1.

令g(x)=lnx-x+1,则所以f(x)在 (0,1)单调递增,在(1,+∞)单调递减,g(x)≤g(1)=0,故a=1符合题意.

解法7(视角7利用函数最值与函数极值的关系)易发现f(1)=0,所以f(x)≥0恒成立等价于f(x)的最小值为f(1),由函数最值与函数极值的关系得f(1)也是函数f(x)的极小值,所以f′(x)=1-a=0,a=1.余下只须证明当a=1时,不等式a(x-1)≥lnx成立.下同解法6.

点评 “f(1)是函数f(x)的极小值”是“f(1)是函数f(x)的最小值”的必要不充分条件,解法7先利用必要条件“f(1)是函数f(x)的极小值”求出参数a的值,再证明所求a的值满足充分性.

(2)令n=3,得

所以m的最小值为3,第(2)问等价于证明不等式

证法1(视角1 数学归纳法)与正整数有关的命题,我们不妨用数学归纳法去证,若直接使用数学归纳法,从k到k+1,右边常量不变,但左边变大,显然是行不通的,于是可考虑证明原不等式的加强命题,由于不等式左边与2n有关,因此可尝试把原不等式加强为

取n=1,得解得t≤3,取t=3,将原不等式加强为

于是可用数学归纳法证得加强命题成立.

①当n=1时,,命题成立;

②假设n=k时命题成立,即

则当n=k+1时,

故当n=k+1时命题也成立.从而原不等式成立.

证法2(视角2比商法)若直接利用比商法证明原不等式行不通,可用比商法证明加强不等式

故数列{an}递减,所以an≤a1=1,故原不等式成立.

点评 数列积式不等式a1a2...an＜(或＞)f(n),一般可构造新数列后通过判断数列{cn}的单调性来证明不等式.

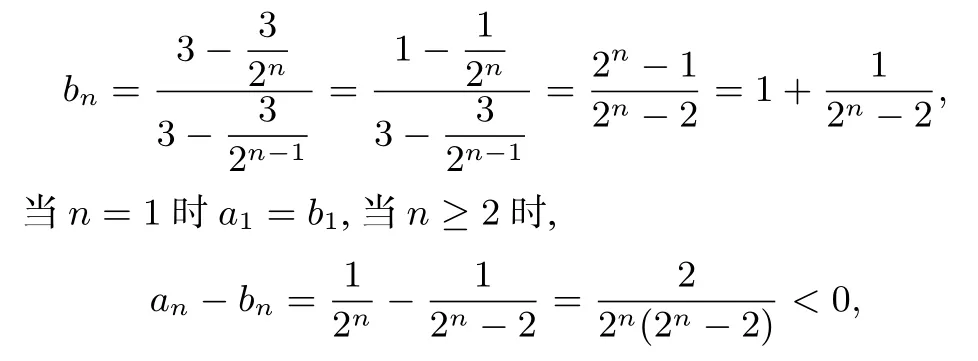
即an＜bn,故a1a2···an≤b1b2···bn,从而原不等式成立.

点评 对于a1a2...an＜(或＞)f(n)型不等式,令

若能证明ak＜(或＞)bk(k=1,2,...,n),则欲证的不等式成立,这种思路朴素,可操作性强,对于“积式”不等式,往往行之有效.

证法4(利用糖水不等式放缩)当n≥2时,

所以当n≥2时,

证法5(视角5倒数变换)不等式等价于由贝努利不等式“若x＞-1,n∈N+,则(1+x)n≥1+nx”的推广：“若实数xi＞-1(i=1,2,...,n)并且它们同正或负,则(1+x1)(1+x2)...(1+xn)≥1+x1+x2+···+xn,”得当n≥2时,

证法6(视角6构造对称式)令

则当n≥2时,

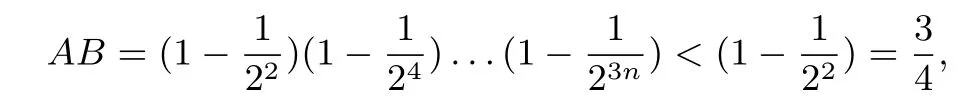
再次贝努利不等式的推广形式得

故原不等式成立.

点评 “积式a1a2...an＞(或＜)Tn不等式”,两边取对数后可转化为“和式lna1+lna2+···+lnan＞(或＜)lnTn不等式”.

证法8(视角8利用均值不等式)因为

所以由均值不等式得

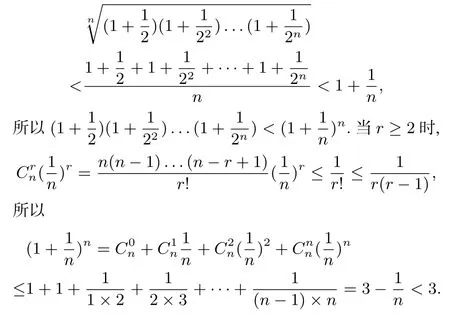
3 题源探寻

笔者在研究上述高考试题时,感觉似曾相识,发现它是2011年“北约”自主招生题与2012年第八届北方数学奥林匹克试题第6题的拓展与延伸.

题2(2011年“北约”自主招生题)已知函数f(x)=

(1)求数列{xn}的通项公式;

题3(2012年第八届北方数学奥林匹克试题第6题)设n是正整数,证明

我们先看题1第(2)问的命制过程：我们来考察题2第

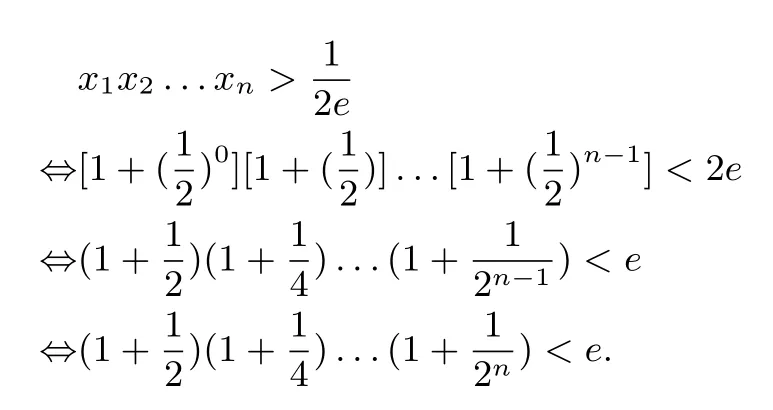
这就是题1第(2)问中不等式

的命制背景,所以m的最小值为3.

由此可见,成题改编是高考命题的一种常见方法,也是一条命题的捷径,这就提示人们在高三备考的过程中要深入细致地研究往年高考试题、自主招生试题及竞赛试题,对各试题我们既要从它们不同的外表下寻求其共性,又要针对某一个试题找出它的个性,对于一道试题我们不能只看到一道试题,还要思考它还能怎么考,这样既发散了思维,又使我们的备考有更好的针对性,提高了备考的效率.

4 问题推广

利用证法7的思路可将原命题推广为：

结论1设a＞1,且n是正整数,证明

结论2 设xk＞-1(k=1,2,...,n),且x1,x2,...,xn不同时为0,证明：

利用贝努利不等式的推广式可将原命题推广为：

结论3设a＞1,且n为正整数,证明

5 推广结论应用

题4(2006年高考江西卷理22)已知数列{an}满足

(1)求数列{an}的通项公式;

(2)证明：对于一切正整数n,a1·a2·····an＜2·n!.

(2)证明：据(1)得,

为证a1·a2·····an＜2·n!,只需证n∈N+时有