余文利,余建军,方建文

1(衢州职业技术学院 信息工程学院,衢州 324000)2(衢州学院 电气与信息工程学院,衢州 324000)

基于改进高斯核度量和KPCA的数据聚类新方法①

余文利1,余建军1,方建文2

1(衢州职业技术学院 信息工程学院,衢州 324000)2(衢州学院 电气与信息工程学院,衢州 324000)

大多数超椭球聚类(hyper-ellipsoidal clustering,HEC)算法都使用马氏距离作为距离度量,已经证明在该条件下划分聚类的代价函数是常量,导致HEC无法实现椭球聚类.本文说明了使用改进高斯核的HEC算法可以解释为寻找体积和密度都紧凑的椭球分簇,并提出了一种实用HEC算法-K-HEC,该算法能够有效地处理椭球形、不同大小和不同密度的分簇.为实现更复杂形状数据集的聚类,使用定义在核特征空间的椭球来改进K-HEC算法的能力,提出了EK-HEC算法.仿真实验证明所提出算法在聚类结果和性能上均优于K-means算法、模糊C-means算法、GMM-EM算法和基于最小体积椭球(minimum-volume ellipsoids,MVE)的马氏HEC算法,从而证明了本文算法的可行性和有效性.

数据聚类; 超椭球聚类; 最小体积椭球; 核主成分分析; 高斯核

聚类作为一种重要的数据分析手段,是机器学习、模式识别、计算机视觉和数据挖掘等领域的研究热点[1].聚类分析就是把对象按照性质上的亲疏程度分多个类或簇,使得簇内的数据具有较高的相似度,簇间的数据具有较高的相异度[2].尽管许多研究者在不断努力,但目前仍没有一种能够处理所有聚类问题的最优算法,聚类仍然是一个困难和具有挑战性的问题.

传统的聚类算法如K-means、GMM-EM、模糊C-means(FCM)等,都是基于最小化簇内样本点的欧氏距离和的通用聚类准则,基于欧氏度量的聚类算法倾向于将样本点划分到相同大小、相同密度和球形的分簇中,这些算法无法完成大而细长的分簇的划分,而现实世界的数据常常以混合高斯分布的形式呈现,如椭球形或其他复杂形状.为解决上述问题,人们提出了各种超椭球聚类算法(hyper-ellipsoidal clustering,HEC)[3-10],这些算法通常使用马氏距离作为距离度量来建立椭球分簇.现有的HEC算法主要存在以下问题:1)过高的计算复杂度,导致在马氏距离中直接计算协方差矩阵非常困难; 2)当分簇包含少量样本点时,协方差矩阵可能是奇异的.为了克服以上的不足,文献[3-5]提出基于改进马氏距离和伪协方差矩阵的HEC算法,但是这些算法的时间复杂度仍然很高.另一方面,文献[8-10]通过近似分簇体积,即找到最小体积椭球(minimum-volume ellipsoids,MVE),取代了协方差矩阵的计算,部分克服了以上的不足.以上大多数方法都是使用马氏距离作为距离度量,已经证明直接将马氏距离应用于聚类不能获得椭球聚类[7],而且划分聚类的代价函数也无法限定分簇的大小和分簇之间的关系.此外,因为这些算法在聚类时无需考虑样本集的密度,所以基于MVE的HEC算法只有等密度分簇的情况才能工作得很好.

本文的目标是实现椭球聚类并给出改进的实用HEC算法的实现,首先,提出了使用改进高斯核度量的基于MVE的K-HEC算法,该算法能够处理椭球形状、不同大小和密度的分簇.为了增强K-HEC算法的能力,通过在特征空间中映射椭球,提出了EK-HEC算法,该算法能够处理非线性和细长结构的分簇.在模拟数据集和标准评测数据集上的仿真实验表明,本文算法在聚类结果和性能上与K-means算法、模糊C-means算法、GMM-EM算法和马氏MVE-HEC算法相比有了很大的提高,从而验证了本文算法在处理椭球形或复杂形状数据集聚类时的可行性和有效性.

1 问题定义

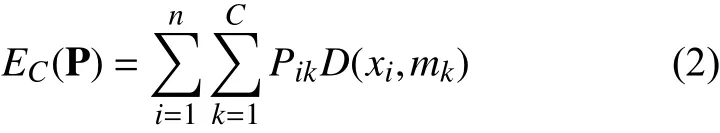
其中D(xi,mk)为输入模式与第k个分簇mk的均值向量之间的距离度量.

为了构造椭球分簇,HEC算法通常采用马氏距离.然而在该条件下,划分聚类的代价函数是常量[7].为了实现椭球聚类,本文使用式(3)的改进高斯核作为距离度量

其中mk和Qk分别是第k个分簇的均值向量和协方差矩阵.变量α∈[0,1]控制着式(3)的第1项和第2项的权重.式(3)的第1项表示马氏距离,第2项与由协方差矩阵Qk表示的第k个椭圆分簇的容积成正比.则聚类代价函数改写为

代价函数EC(P)达到最优的必要条件为通过最小化式(4)得到划分的分簇中心表示为

证毕.

定理1.如果改进高斯核式(3)作为式(2)的聚类代价函数的距离度量,则

证毕.

2 椭球和复杂形状聚类

本文提出了两种最小化分簇体积权重和的HEC算法—K-HEC算法和EK-HEC算法.其中K-HEC算法是使用改进高斯核和MVE近似的迭代HEC算法,它将样本划分到指定数量的椭球分簇中; EK-HEC算法是K-HEC算法的扩展,它通过使用定义在核特征空间的椭球来改善K-HEC算法的聚类能力,以便能处理更复杂形状样本集的聚类.

2.1 K-HEC算法

K-HEC算法开始于一个初始的聚类,最终将初始的聚类划分为C个分簇,在此过程中算法迭代查找改进的划分矩阵的分配,分簇体积的权重和不断缩小,直到分簇结果没有进一步可能的改进为止.

因此,本文使用三个近似方法来寻找MVE.首先,推导式(9)所示的Löwner-John椭球体[11]凸优化问题,该问题可以几何解释为最小化椭球体的体积.

其次,通过近似计算包含矩阵Q特征向量和的目标函数来求解式(10)所示凸优化问题[8,11].

最后,使用Khachiyan的快速近似算法[12]来寻找MVE.

算法1.K-HEC算法输入:d维空间的n个样本输出:划分矩阵P步骤1.确定分簇数C,从样本集中随机选择C个样本,设定为分簇的中心,记作mk;步骤2.首先使用样本与分簇中心mk欧氏距离来确定划分矩阵的初始分配x={xi∈Rd}n i=1■■■■■Pik=1,ifDEuc(xi,mk)＜DEuc(xi,mj),j=1,2,...,Candj≠k Pik=0,otherwise步骤3.计算新的分簇中心和属于该分簇的样本的数量mk=∑n∑ni i=1Pikxi=1Pik,nk=∑n i=1Pik步骤4.使用MVE近似算法计算伪协方差矩阵Qk;步骤5.使用式(3)的改进高斯核度量、mk和Qk确定划分矩阵P的一个新的分配{Pik=1,ifDMGK(xi,mk;Qk)＜DMGK(xi,mj;Qj)Pik=0,otherwise步骤6.如果划分矩阵P没有变化,则算法停止.否则重复步骤3到步骤5.

2.2 EK-HEC算法

大部分划分聚类算法在对非线性和细长结构数据集进行聚类时,不能取得理想的效果,为此人们提出了谱聚类算法[13]和核方法[14].为了在非线性和细长结构数据集上执行聚类,本文使用了核主成分分析(Kernel principal component analysis,KPCA).通过RBF核函数,能够有效地在与基于非线性映射的输入空间相关联的高维特征空间中计算主成分.KPCA的原理如下所示.

EK-HEC算法通过在核空间中执行K-HEC算法实现复杂形状聚类,算法的具体描述如算法2.

算法2.EK-HEC算法输入:d维空间的n个样本输出:划分矩阵P Kij=Φ(xi)·Φ(xj)=K(xi,xj);x={xi∈Rd}n i=1步骤1.计算核矩阵K,i,j = 1,2,...,n;步骤2.解式(12),找到非零的特征值;步骤3.使用非零特征值αk(k=1,2,…,p),计算样本Ф(x)在特征向量Vk上的投影;˜x=(Vk·Φ(x))=∑n i =1αkiK(xi,x)步骤4.确定分簇数C,在特征空间中随机选择C个样本,将它们设置为分簇的中心,记作 ;˜mk ˜mk步骤5.使用欧氏距离计算样本与分簇中心 的距离,确定划分矩阵P的初始分配■■■■■Pik=1,ifDEuc(˜xi,˜mk)＜DEuc(˜xi,˜mj),j=1,2,...Candj≠k Pik=0,otherwise步骤6.计算新的分簇中心和属于新分簇的样本数˜mk=∑ni=1Pik˜xi/∑n i=1Pik,nk=∑n i=1Pik ˜Qk步骤8.使用式(3)的改进高斯核度量、 和 确定划分矩阵P的新的分配步骤7.使用MVE近似算法计算伪协方差矩阵 ;˜mk ˜Qk■■■■■Pik=1,ifDEuc(˜xi,˜mk;˜Qk)＜DEuc(˜xi,˜mj;˜Qj),j=1,2,...Candj≠k Pik=0,otherwise步骤9.如果划分矩阵P没有变化,则算法终止; 否则重复步骤6至步骤8.

3 仿真实验

3.1 实验描述

为验证K-HEC算法和EK-HEC算法的有效性,在模拟数据集和基准评测数据集上进行了实验.K-HEC算法和 EK-HEC 算法是在 Matlab 上使用CVX[15]和LMI工具箱编程实现,在Intel(R)Xeon® CPU W5590@line-height:15.5pt3.33GHZ的微机Windows XP环境下运行.在性能评估时,使用误分类率(Misclassification rate,MCR)和归一化互信息(Normalized mutual information,NMI)作为评价指标,分别定义如下

其中X、Y是两个随机变量,I(X,Y)是互信息,H(X)和H(Y)是X和Y的熵.

3.2 实验结果与分析

3.2.1 模拟数据集

为了说明本文所提出算法的有效性,在实验中使用了2个模拟数据集(具体描述如表1所示).模拟数据集1用以验证K-HEC算法对于不同大小、不同密度和椭圆形分簇的聚类能力,该数据集包含一个圆形的分簇和一人细长椭圆形的分簇.K-HEC算法在模拟数据集1上使用式(9)-式(11)三种不同的MVE近似方法所提到的聚类结果是一样的,因此忽略式(9)和式(10)的方法,使用式(11)方法的K-HEC算法在数据集1上的聚类结果如图1所示.

表1 模拟数据集

图1 不同算法在模拟数据集1上的聚类结果

从图1(b)可以看出,K-means算法在模拟数据集1上不能得到正确的聚类; 从(c)可以看出,马氏HEC算法虽然将样本划分为不同大小的两个椭圆分簇,但当两个分簇距离较近时聚类结果也不准确; (d)表明本文提出的K-HEC算法通过调整α的值来控制改进高斯核的第1项和第2项的权重,从而最小化分簇体积权重和,使得聚类后分簇的紧凑性和密度达到最大.

模拟数据集2包含一个高斯分布分簇和一个香蕉形分簇,用于验证EK-HEC算法的有效性,该算法专门设计用于复杂几何形状样本集的聚类.K-means算法、HEC算法、K-HEC算法和EK-HEC算法在模拟数据集2上的聚类结果如图2(b)～(f)所示.

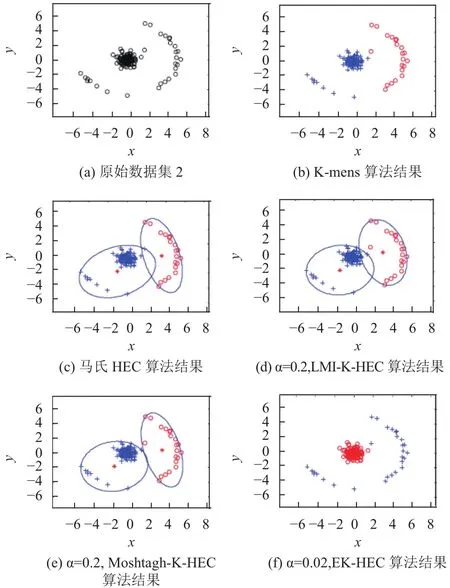
图2 不同算法在模拟数据集2上的聚类结果

从图2可以看出,K-means算法、马氏HEC算法以及K-HEC算法有相似的聚类结果.可以注意到,虽然聚类结果相似,但是由每个算法所确定的聚类的决策边界仍有很大的不同.与其他算法相比,基于Moshtagh方法的MVE近似的Moshtagh-K-HEC算法建立了清晰的决策边界,而马氏HEC算法和LMI-K-HEC算法有重叠的决策边界.EK-HEC算法按照预期找到了正确的分簇,仅有一个样本错分.图3描述了EK-HEC算法在模拟数据集2上的聚类结果,其中(a)和(b)分别描述了在算法在输入空间和特征空间的聚类结果,映射到特征空间的样本得到很好的分离,并且能够通过椭圆的决策边界实现聚类.

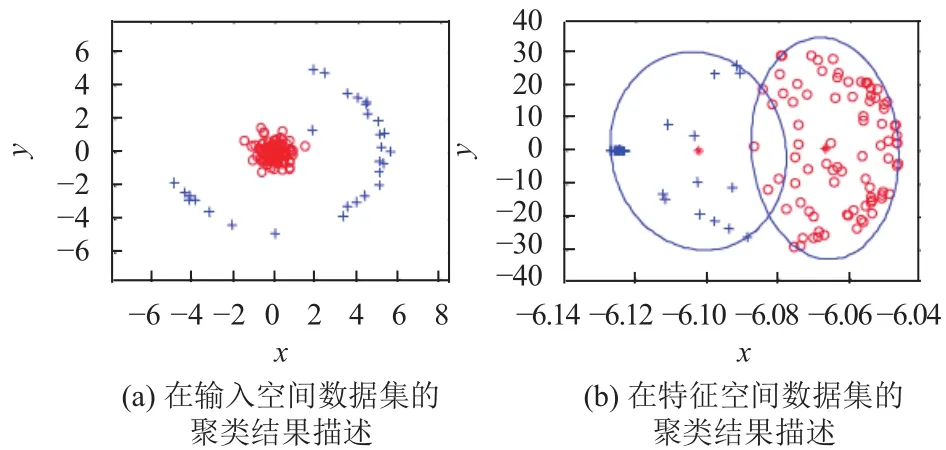
图3 EK-HEC算法在模拟数据集2上的聚类结果

3.2.2 基准评测数据集

为了评估本文提出算法的性能,在来自UCI的3个基准评测数据集(具体描述见表2)上与K-means算法、模糊C-means算法、GMM-EM算法和马氏距离MVE-HEC算法进行了比较实验.6种算法在MCR和NMI两个评判准则上的比较结果如图4所示,由图4可知,K-HEC算法在MCR和NMI两个指标上均优于K-means、模糊C-means、GMM-EM和HEC算法,EK-HEC算法与其他算法相比有更好或类似的聚类性能.

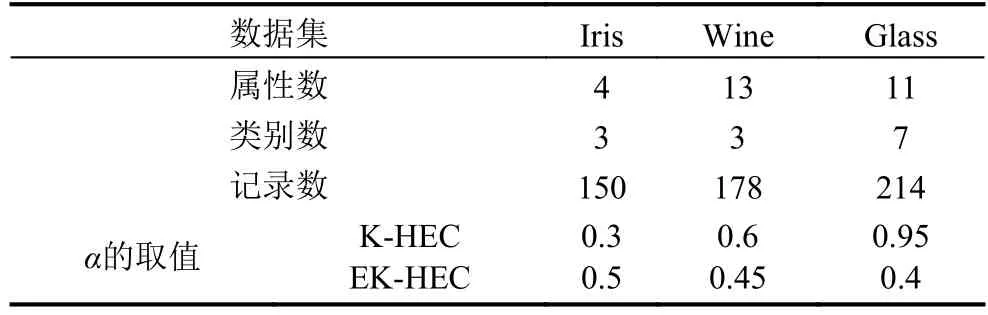
表2 来自UCI的基准评测数据集

4 结语

本文将基于MVE的HEC算法与改进的高斯核相结合,提出了K-HEC算法,通过应用定义在核空间的椭圆聚类,增强了K-HEC算法聚类能力,提出了EK-HEC算法.K-HEC算法能够处理不同大小、不同密度和椭球形壮的分簇,EK-HEC算法能够处理非线性和细长结构的复杂几何形状的分簇.在模拟数据集和UCI基准评测数据集上的仿真实验表明,K-HEC算法能够通过建立紧凑的分类边界有效地分离各分簇,EK-HEC算法在非线性和细长结构的数据集上完成了正确的聚类.本文算法无论在聚类能力和性能方面均优于K-means、模糊C-means、GMM-EM和HEC算法,从而验证了本文算法的可行性和有效性.

图4 基准评测数据集上的聚类性能比较

1Duda RO,Hart PE,Stork DG.Pattern Classification.New York:John Wiley & Sons,2012.

2Nagpal A,Jatain A,Gaur D.Review based on data clustering algorithms.Proc.of the 2013 IEEE Conference on Information & Communication Technologies (ICT).JeJu Island,Korea.2013.298–303.

3Mao JC,Jain AK.A self-organizing network for hyperellipsoidal clustering (HEC).IEEE Trans.on Neural Networks,1996,7(1):16–29.[doi:10.1109/72.478389]

4Wang S,Ma F,Shi W,et al.The hyperellipsoidal clustering using genetic algorithm.Proc.of the 1997 IEEE International Conference on Intelligent Processing Systems.Beijing,China.1997,1.592–596.

5Ichihashi H,Ohue M,Miyoshi T.Fuzzy C-means clustering algorithm with pseudo Mahalanobis distances.Proc.of the 3rd Asian Fuzzy Systems Symposium.Changwon,Korea.1998.148–152.

6Moshtaghi M,Rajasegarar S,Leckie C,et al.An efficient hyperellipsoidal clustering algorithm for resource-constrained environments.Pattern Recognition,2011,44(9):2197–2209.[doi:10.1016/j.patcog.2011.03.007]

7Wang S,Xia SW,Mao JC,et al.Comments on “a self-organizing network for hyperellipsoidal clustering (HEC)”.IEEE Trans.on Neural Networks,1997,8(6):1561–1563.[doi:10.1109/72.641479]

8Lee HS,Park JY,Park DH.Hyper-ellipsoidal clustering algorithm using linear matrix inequality.Journal of Korean Institute of Intelligent Systems,2002,12(4):300–305.[doi:10.5391/JKIIS.2002.12.4.300]

9Kumar M,Orlin JB.Scale-invariant clustering with minimum volume ellipsoids.Computer & Operations Research,2008,35(4):1017–1029.

10Shioda R,Tunçel L.Clustering via minimum volume ellipsoids.Computational Optimization and Applications,2007,37(3):247–295.[doi:10.1007/s10589-007-9024-1]

11Boyd S,Vandenberghe L.Convex optimization.Cambridge,UK:Cambridge University Press,2004.

12Todd MJ,Yildirim EA.On Khachiyan’s algorithm for the computation of minimum-volume enclosing ellipsoids.Discrete Applied Mathematics,2007,155(13):1731–1744.[doi:10.1016/j.dam.2007.02.013]

13Cao JZ,Chen P,Zheng Y,et al.A max-flow-based similarity measure for spectral clustering.ETRI Journal,2013,35(2):311–320.[doi:10.4218/etrij.13.0112.0520]

14Shawe-Taylor J,Cristianini N.Kernel methods for pattern analysis.Cambridge,UK:Cambridge University Press,2004.

15CVX Research,Inc.CVX:Matlab software for disciplined convex programming,version 2.0.http://cvxr.com/cvx.[2013-04].

Novel Data Clustering Method Based on A Modified Gaussian Kernel Metric and Kernel PCA

YU Wen-Li1,YU Jian-Jun1,FANG Jian-Wen21(College of Information Engineering,Quzhou College of Technology,Quzhou 324000,China)2(College of Electrical and Information Engineering,Quzhou University,Quzhou 324000,China)

Most hyper-ellipsoidal clustering(HEC)algorithms use the Mahalanobis distance as a distance metric.It has been proven that HEC,under this condition,cannot be realized since the cost function of partitional clustering is a constant.We demonstrate that HEC with a modified Gaussian kernel metric can be interpreted as a problem of finding condensed ellipsoidal clusters(with respect to the volumes and densities of the clusters)and propose a practical HEC algorithm named K-HEC that is able to efficiently handle clusters that are ellipsoidal in shape and that are of different size and density.We then try to refine the K-HEC algorithm by utilizing ellipsoids defined on the kernel feature space to deal with more complex-shaped clusters.Simulation experiments demonstrate the proposed methods have a significant improvement in the clustering results and performance over K-means algorithm,fuzzy C-means algorithm,GMM-EM algorithm and HEC algorithm based on minimum-volume ellipsoids using Mahalanobis distance.

data clustering; hyper-ellipsoidal clustering; minimum-volume ellipsoids; kernel PCA; Gaussian kernel

余文利,余建军,方建文.基于改进高斯核度量和KPCA的数据聚类新方法.计算机系统应用,2017,26(10):150–155.http://www.c-sa.org.cn/1003-3254/5988.html

2017-01-11; 采用时间:2017-02-15