张欣欣,刘 萍

(哈尔滨师范大学)

具有非线性捕获量的捕食-食饵模型的动力学分析

张欣欣,刘 萍

(哈尔滨师范大学)

研究了具有HollingⅡ型响应函数捕获量的捕食-食饵模型.应用比较原理和最大值原理给出了正稳态解的先验估计.应用庞加莱不等式证明了稳态方程的非常数稳态解的不存在性.

非线性捕获量; 捕食-食饵模型; 非常数稳态解; 先验估计

0 引言

物种间相互作用的研究对生物资源的开采和种群的收获等方面起着重要的作用.在过去的几十年里,提出并研究了大量的捕食-食饵模型.捕食-食饵模型最开始由美国的生态学家Lotka[1]和意大利的数学家Volterra[2]提出.其形式为:

(1)

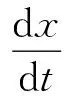
(2)

其中k是食饵的最大承载量,a是捕食者捕获食饵的接触率,m是吃的食饵变成新的捕食者的转化率.

单纯的微分方程无法全面的描述生物系统的某些性质,具有时滞、扩散、捕获率等现象的捕食-食饵模型能丰富系统的动力学行为.捕获量是研究种群动力学行为的一个重要的因素,研究具有捕获量的捕食-食饵模型对保护生态资源具有很大的意义.

近几十年来,很多学者研究了带有收获率的捕食-食饵模型.文献[3]研究了捕食者带有常数捕获量的生物模型在平衡点处发生的Bogdanov-Takens分歧与Hopf分歧.文献[4]研究了食饵带有常数收获率的捕食-食饵模型的解的不稳定性.文献[5]分析了单个种群带有成比例收获率的模型,分别研究了正解的全局渐近稳定性和周期解的存在性、唯一性与稳定性.文献[6]研究了食饵种群具有Michaelis-Menten型收获率的捕食食饵系统的分歧和稳定性.文献[7]详细地分析了捕食者带有非线性捕获量的模型的平衡点的分歧与稳定性等性质.

2015年Gupta等在文献[8]中提出在系统(2)的基础上带有非线性捕获量的模型为:

研究表明带有捕获量的捕食-食饵模型可以展示非常复杂的动力学行为.系统能发生许多类型的分歧,例如:鞍结点分歧,Hopt-Andronow分歧,跨越分歧和Bogdanov-Takens分歧.通过计算第一个Lyapunov数能得到Hopf分歧周期解的稳定性,通过数值模拟当Hopf分歧曲线和一个鞍结点相交产生极限环显示了同宿环的存在性.

对系统(3)非量纲化,令

系统(3)转化为:

因为物种要进行迁移扩散运动,进一步,系统(4)转化为系统(5),

其中Δ为拉普拉斯算子,Ω⊂Rn是具有光滑边界∂Ω的有界区域.

1 先验估计

设系统(5)相应的稳态方程为系统(6)

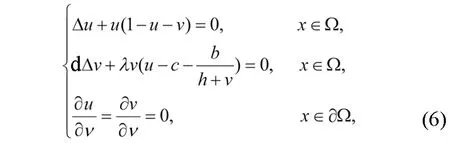
该部分将考虑系统(6)的稳态解的一些性质.首先分析系统(6)的稳态解的有界性.

定理1.1 设d,λ,c,b,h>0,Ω⊂Rn是具有光滑边界∂Ω的有界区域.假设(u,v)是系统(6)的正稳态解,则

(7)

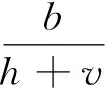
设

则有

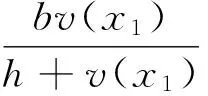
故,

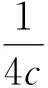
因此，

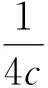
2 非常数稳态解的非存在性

该部分将证明稳态方程(6)的非常数稳态解的不存在性.

引理2.1 (庞加莱不等式)令Ω是Rn中的一个有界连通开子集,并且∂Ω是C1的,如果

定理2.2 设d,λ,c,b,h>0,Ω⊂Rn是具有光滑边界∂Ω的有界区域.存在常数

(8)

其中

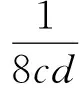
(9)

当min{1,d}>D*时,则系统(6)只有非负常数解.

证明设(u,v)是系统(6)的非负解,令

由定理1.1,有

由Green公式,有

分别对Ii(i=1,2)进行估计,有

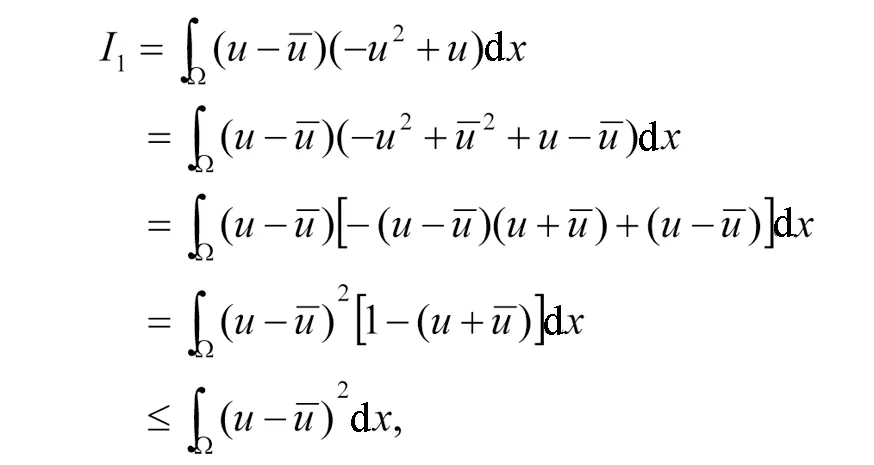
和

由上可知

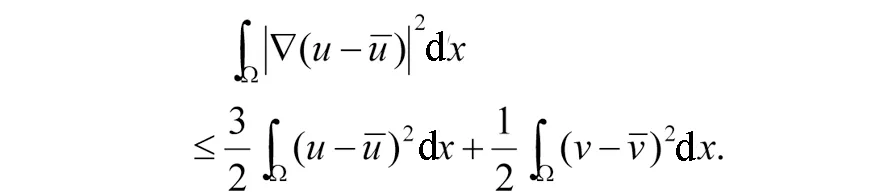
分别对Ji(i=1,2,3)进行估计,有

和

由上可知

由引理2.1,有

其中A和B由(9)式所定义.当min{1,d}>D*时,有

因此(u,v)只能是常数解.

[1] Lotka A J.Analytical Note on Certain Rhythmic Relations in Organic Systems.Proc Natl Acad Sci,1920(6):410-415.

[2] Volterra V.Variazioni e Fluttuazioni Del Numero d’ individui in Specie Animali Conviventi[J].Mem R Accad Naz dei Lincei Ser,1926(2):31-113.

[3] Xiao D,Ruan S.Bogdanov-Takens Bifurcations in Predator-Prey Systems with Constant Rate Harvesting[J].Fields Inst Commun Ser,1999(21):493-506.

[4] Martin A,Ruan S.Predator-Prey Models with Delay and Prey Harvesting[J].Math Biol,2001,43(3):247-267.

[5] 郭红建,叶凯莉.一类具有成比例收获的红松林模型的最优问题.信阳师范学院学报:自然科学版,2012,25(4):438-441.

[6] Li Y,Wang M.Dynamics of a Diffusive Predator-Prey Model with Modified Leslie-Gower Term and Michaelis-Menten Type Prey Harvesting[J].Acta Appl Math,2015,140(1):147-172.

[7] Wang X,Wang Y.Novel Dynamics of a Predator-Prey System with Harvesting of the Predator Guided by Its Population Appl Math Model,,2017:636-654.

[8] Gupta R P,Chandra P,Banerjee M.Dynamical Complexity of a Predator-Prey Model with Nonlinear Predator Harvesting.Discrete Contin.Dyn[J].Syst Ser B,2014(20):423-443.

[9] 王明新.非线性椭圆型方程[M].北京:科学出版社,2010.

Abstract:In this paper,a predator-prey model with Holling Ⅱ response function harvesting is studied.A priori estimate of positive steady state solutions are given by applying the comparison and maximum principle.Nonexistence of non-constant steady state solutions of the steady state equation is proved by applying the Poincare inequalities.

Keywords:Nonlinear harvesting; Predator-prey model; Non-constant steady state

(责任编辑：季春阳)

DynamicsAnalysisofaPredator-PreyModelwithNonlinearHarvesting

Zhang Xinxin,Liu Ping

(Harbin Normal University)

O19

A

1000-5617(2017)02-0009-04

2017-01-12