海波，姚海龙，孟丛丛

（兰州城市学院 电子与信息工程学院，兰州 730070）

使用轴承振动信号进行故障诊断是常用的故障诊断方式，振动信号的特征提取和故障识别则是滚动轴承故障诊断的重要步骤［1-3］。

在特征提取方面，近似熵（Approximate Entropy，AE）与样本熵（Sample Entropy，SE）对信号数据的长度较为敏感，且在熵值的计算过程中需对信号进行2次重构，算法较为复杂［4-7］；排列熵（Permutation Entropy，PE）虽然仅需对信号进行1次重构，但计算过程中仍需要复杂的排序运算［8-10］；基本尺度熵（Base-Scale Entropy，BSE）计算简单、效率高，且具有一定的抗干扰能力，在齿轮故障诊断中有一定的应用［11-13］；然而，上述方法只能检测时间序列信号在单一尺度上的复杂性，而多尺度熵（Multiscale Entropy，ME）能衡量时间序列信号在不同尺度下的复杂性［14-15］，其中多尺度排列熵（Multiscale Permutation Entropy，MPE）模型在滚动轴承信号特征提取中的效果较好［16-17］。

在故障识别方面，GK（Gustafson-Kessel）和GG（Gath-Geva）聚类算法比较常用，但均需要事先划分聚类数目［18-22］；CFS（Clustering by Fast Search）聚类算法［23］简单明快，其根据数据点的局部密度和截断距离对具有跳跃性的数据点进行聚类中心点的选定，不需要聚类数目的划分。

综上所述，虽然ME可获得多尺度的信息，但却存在数据维数高，无法可视化等问题，可采用主成分分析法（Principal Component Analysis，PCA）进行数据降维，从而作为CFS的输入。因此，将多尺度基本熵（Multiscale Base-scale Entropy，MBSE）与CFS聚类算法结合，尝试用于滚动轴承的故障诊断。

1 多尺度基本熵

1.1 基本尺度熵

BSE的计算步骤如下：

1）对于一个给定数据长度的时间序列u()i（1≤i≤N），数据集 Xmi（1≤i≤N-m+1）需进行如下重构

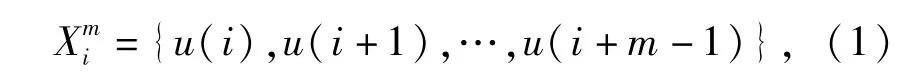
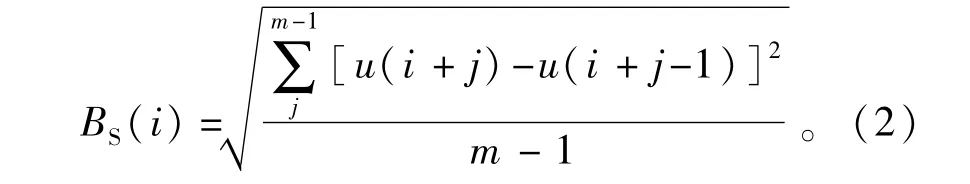
3）对得到的BS值进行符号划分，将转变为符号序列 Si（X（i））＝｛s（i），…，s（i+m-1）｝，s∈ A（1，2，3，4），转换方式为

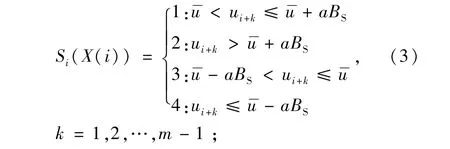
4）统计符号序列Si的概率分布情况P（π），由于Si（X（i））由m维时间序列Xmi形成，且存在4种符号，所以共有4m种不同组合状态π，则统计概率 P（π）为

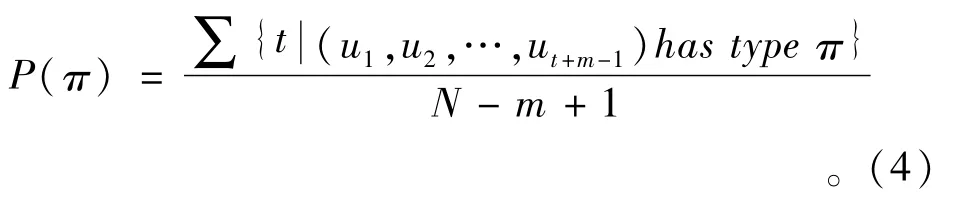
5）计算BSE，其计算式为

1.2 多尺度基本熵

BSE确定的是时间序列在单一尺度上的复杂度和无规则程度，MBSE反映的则是时间序列在不同尺度下的复杂性程度，其定义为时间序列在不同尺度下的BSE，其中多尺度通过粗粒化过程获得，具体的计算步骤如下：

1）对于原始数据Xmi，建立新的粗粒向量为

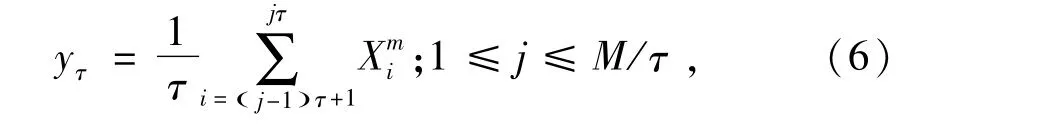
式中：τ为尺度因子（τ＝1，2，…），若 τ＝1则为原始数据；M为样本总数。对于非零原始序列Xmi，其被分为τ个每段长M／τ的粗粒序列yj（τ）。

2）分别计算τ个粗粒序列为yj（τ）的 BSE，形成MBSE。

2 主成分分析

MBSE模型提取的信号维度较高，存在数据冗余、计算效率低、无法可视化等问题，而PCA可以抽取数据的主要成分，对特征向量进行降维以作为CFS聚类算法的输入。

对于一个给定的MBSE或MPE矩阵X＝［x1，x2，…，xN］，其中N为样本数量，n为样本的维数，且满足n＜N。其计算步骤为：

3）使用奇异值方法分解协方差矩阵，则Rx＝ATΛA，ATA＝AAT＝I。A＝［A1，A2，…，An］T为矩阵X对应的特征值矩阵，其中Λ＝diag（λ1，λ2，…，λn），是矩阵A按照降序排列的对角矩阵。

4）使用累积贡献率θk确定X的主要成分个数，即

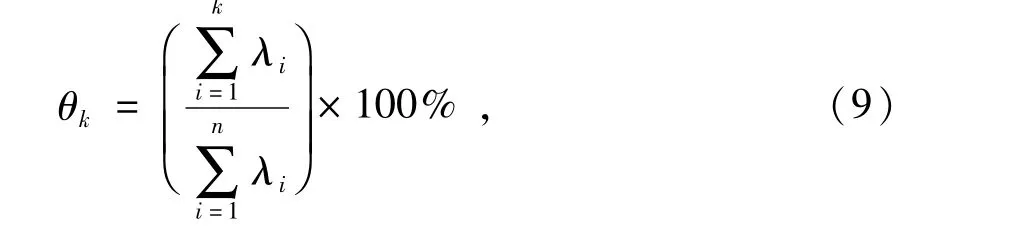
式中：θk为从第1到第k个主要成分的百分比。

3 CFS聚类算法

CFS聚类算法的核心思想在于对聚类中心的刻画上，聚类中心点的特点为：1）自身密度大，即被密度均不超过自己的近邻数据点包围；2）与其他密度更大数据点之间的距离更大。

CFS聚类的详细计算过程［23］如下：

1）设具有N个数据点的数据集合X＝｛x1，x2，…，xN｝，该集合中的任何数据点xi与xj之间的距离为

式中：当xi具有最大局部密度时，δi表示数据集合X中与数据点xi距离最大的数据点与xi之间的距离；否则δi表示在所有局部密度大于xi的数据点中与xi距离最小数据点之间的距离。

4）计算每个数据点的γ值并进行降序排列

5）根据γ确定其聚类中心，γi越大表示成为聚类中心点的可能性越大。故对γ进行降序排列，依次选取γ较大且具有跳跃性的数据点作为聚类中心点，即聚类中心点过渡到非聚类中心点时γ值具有明显的跳跃性。

6）统计每个数据点与聚类中心的距离小于截断距离dc的个数（即ρi），从而实现分类。

4 试验分析

4.1 数据来源

试验轴承为6205-2RS JEM-SKF深沟球轴承，使用电火花技术分别在轴承内圈、外圈、球上设置单点故障［24］。本试验选用的故障直径为0.177 8 mm，电动机功率为1 496W，转速为1 750 r／min，采样频率为12 kHz。在此情况下采集到正常（NR），内圈故障（IRF），外圈故障（ORF）和球故障（BF）4种状态的振动信号。

4.2 参数设置

BSE：嵌入维数 m的取值范围一般为3～7［11-13］，且要满足 4m≤ N条件（N为序列的长度）；参数 a一般取值为0.1～0.4［11-13］；根据轴承振动信号的特性，选择m＝4，a取值为0.2或0.3。

MBSE：尺度因子 τ一般设置为 20［15-17］，振动信号的长度统一取为N＝2 048。

CFS：需选取一个阶段距离参数dc，使得每个数据点的平均近邻数据点（即距离不超过dc的数据点）约占数据点总数的1%～2%。dc设置太大，会使每个数据点xi的局部密度数值ρi较大，导致区分度不高；若dc设置过小，则会导致同一个簇类被拆分成多个［23］。综合考虑，设置dc为比例k／M＝1.5%情况下的数值。

4.3 试验流程

试验流程如图1所示，主要步骤为：

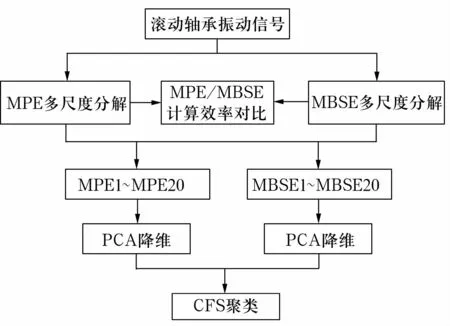
图1 试验流程Fig.1 Experimental flow chart

1）预先设置模型的参数；

2）使用MBSE模型对采集的振动信号进行多尺度分解，得到不同尺度因子下的MBSE值；

3）统计MBSE的计算总时间和平均时间，进行计算效率对比；

4）使用PCA方法进行数据降维，选择（9）式中的参数k＝2时的主要成分作为CFS聚类模型的输入；

5）与MPE模型进行对比分析。

4.4 对比分析

对采集到4种状态的实际振动信号进行编号：NR为 1～50，IRF为51～100，BF为 101～150，ORF为151～200。每种状态下振动信号某一样本的幅值如图2所示。从图中可以看出：NR和BF的信号没有明显的周期性，这是由于NR和BF振动信号的随机性较强，故两者的自相似性较低，两者难以区分；IRF和ORF信号具有较为明显的振动规律，这是由于两者的自相似性较高，特别是内圈固定、外圈转动时的振动规律更加明显，但这2种信号的振动规律相似，也难以区分。

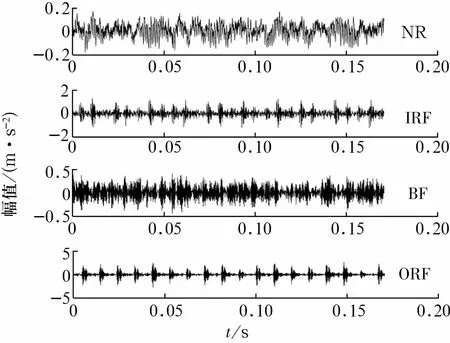
图2 轴承不同故障状态下的振动信号Fig.2 Vibration signals of rolling bearing under different faults

为准确进行故障识别，需进一步提取信号的特征向量，根据预先设置的参数，使用MPE／MBSE模型对实际振动信号进行多尺度分解，得到的不同尺度因子下的熵值，如图3所示。

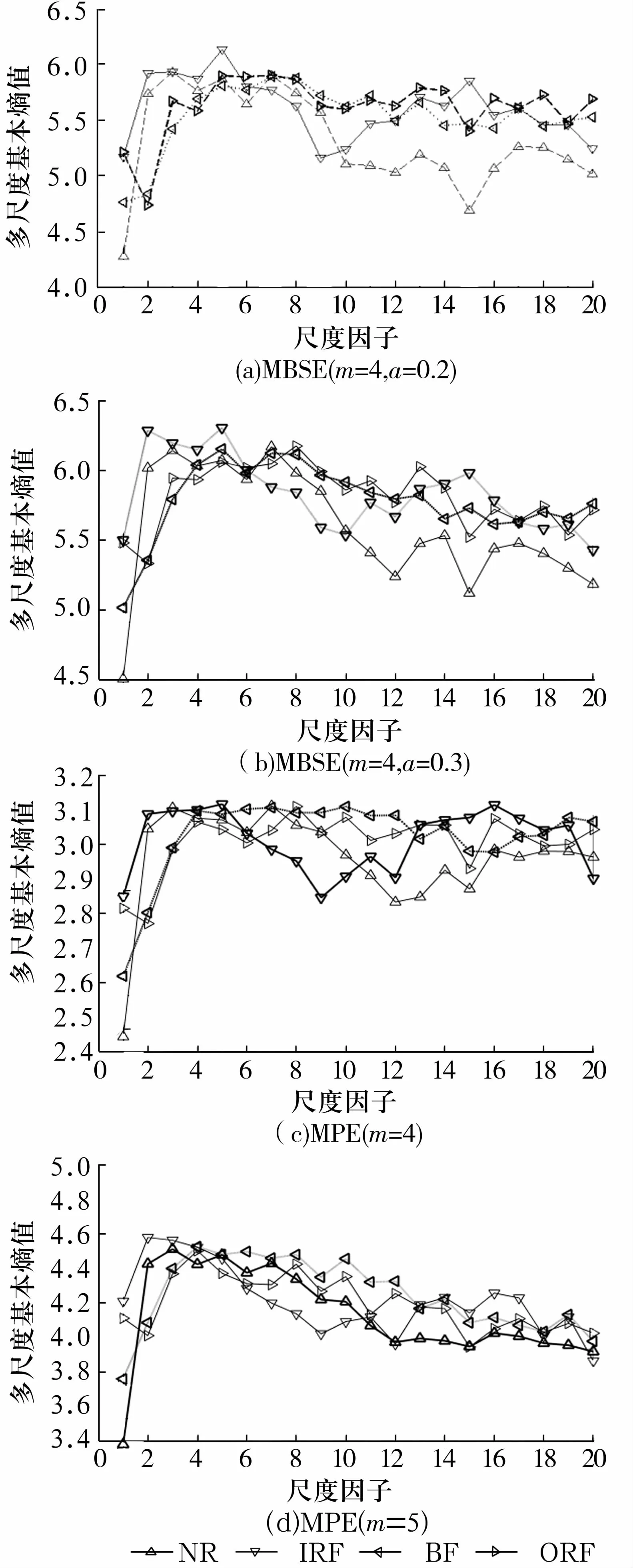
图3 多尺度分解结果Fig.3 Multi-scale decomposition results

从图3中可以看出，MBSE与MPE值整体上呈现减小的趋势，因为振动信号在分解之后，频率依此从高到低，故呈现减小趋势，表明其信息主要包含在尺度因子较小的MBSE与MPE值中。经过统计得到：MBSE模型计算用时22.219 8 s，MPE模型计算用时38.246 7 s，即MBSE模型的计算效率较高。主要原因是由于PE模型在统计每种符号序列出现的概率前需要对N-m+1个m维矢量进行升序排序［9-10］，但 BSE模型在统计概率P(π)前只需要计算相邻点数间隔的差值方均根值，不需要进行复杂的排序运算［11-13］；另外，在划分到多尺度上时，需要计算尺度从1～20情况下的PE／BSE值，会加大MPE／MBSE模型的计算时间落差。

由于上述熵值特征矩阵的维度为20，在进行故障识别时会造成数据不易可视化和信息冗余等问题。故使用PCA模型进行降维，根据（9）式计算所得的累计贡献率结果见表1，表中λ1与λ2代表原始数据经过PCA降维后第1～2个特征数值。由表可知，前2个特征数值之和约占总特征数值的80%左右，这是由于特征数值在计算过程中按降序排列，故λ1与λ2基本包含了信号的大部分信息，可选作故障特征向量。

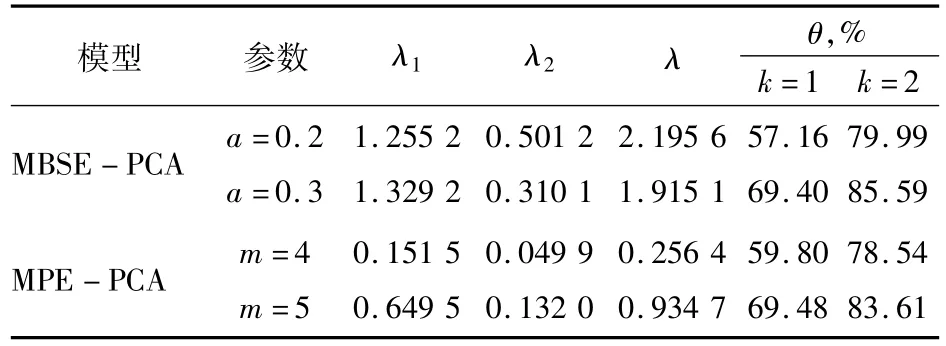
表1 累计贡献率θ随k的数值变化表Tab.1 The value of θ changes with k

随后使用CFS模型对故障特征向量进行聚类，依据（11）～（13）式计算得到200个样本的的聚类中心点的局部密度ρ、距离δ以及γ，结果如图4和图5所示。

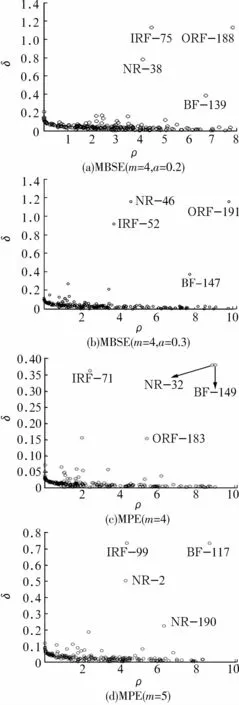
图4 局部密度ρ与距离δFig.4 Local density ρ and distance δ

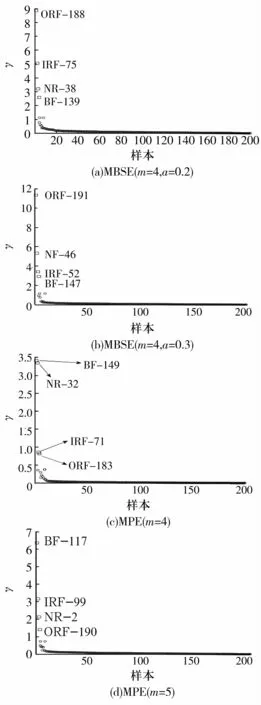
图5 样本点的γ值Fig.5 Sample point of γ

从图中可以看出：1）聚类中心点的局部密度ρ与距离δ的数值明显大于非聚类中心点；2）聚类中心点的γ整体上明显大于非聚类中心点。

其中，γ最小为0.818 4，最大为8.851 4，而非聚类中心点的γ数值几乎为0，其原因如下：

1）对于聚类中心点而言，利用（10）式计算任意样本之间的距离时，聚类中心点之间的距离最大，而（11）式为ρ的减函数，即计算所有样本的局部密度ρ时，聚类中心点之间的距离是最大。设置的阶段距离为1.5%，因此（11）式中的 -（dij／dc）2较小，局部密度数值ρ偏大，非聚类中心点的局部密度ρ与距离δ数值接近于0，与图4的结果相符。

2）利用（13）式计算γ时，由于聚类中心点的局部密度ρ与距离δ远大于非聚类中心点，故得到的γ也大于非聚类中心点。而且图中的聚类中心点具有明显的跳跃性，而非聚类中心点则无此特点，说明应该选择γ数值较大且有跳跃性这些数据点作为聚类中心点。最后的2维聚类结果如图6所示，从图中可以看出，4种故障状态得到了较好的区分，各样本点之间几乎没有重叠现象，聚类中心点被周围样本点围绕的密度较大，中心点相互之间的距离也较大。且样本点与其他中心点之间的距离比与自身中心点之间的距离大，统计数据也表明，CFS模型对试验信号的区分程度近似100%，具有较好的区分效果。

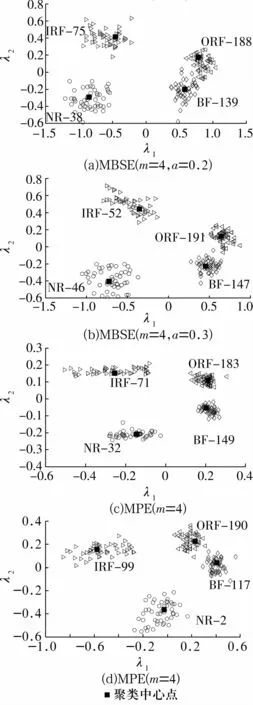
图6 2维聚类结果Fig.6 The 2D clustering results

5 结束语

提出了一种MBSE与CFS相结合的故障诊断方法，并将其应用于滚动轴承的故障诊断。与MPE模型相比，使用MBSE模型对轴承振动信号进行特征提取的计算效率更高，而通过选用不同故障尺寸的轴承样本数据进行试验，表明经过PCA降维处理后，CFS聚类算法可对不同故障类型进行有效的区分。

但也存在不足之处，如CFS聚类算法在选择聚类中心点时选择局部密度ρ与距离δ的乘积作为标准，虽然综合考虑了这2个参数，但两者的数值可能处于不同数量级，是否能通过其他方式综合考虑这2个参数，更好的选择聚类中心抉择则需要进行更深入的研究。