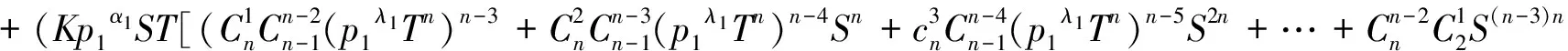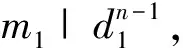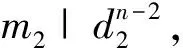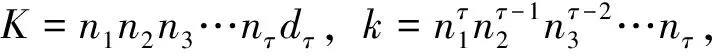李 高

(山西大同大学煤炭工程学院，山西 大同 037003)

Fermat大定理的初等证明

李 高

(山西大同大学煤炭工程学院，山西 大同 037003)

目的 探寻费尔马大定理的初等证明。方法 利用二项式定理展开式、代数方程根与系数的关系，及其初等数论的知识，采用反证的方法，用初等方法对费尔马大定理进行论证。结果 费尔马大定理对任意的正整数n>2时，不定方程xn+yn=zn没有正整数解。结论 费尔马大定理可以用初等方法直接证明其结论的正确性。避弃了烦琐的间接初等证明法，避开了高深的高等解法，在学习和应用时给出了解决问题的思维方式和思路。

不定方程;正整数解;公因子;奇素数;费尔马小定理;费尔马大定理

1 费尔马大定理

1.1 费尔马大定理[1]

对任意的正整数n>2时，不定方程

xn+yn=zn

没有正整数解。

1.2 费尔马大定理简介

1637年，法国数学家费尔马(Pierre de Fermat)在研读1621年巴黎出版的古希腊数学家丢番图“算术”一书时，在该书关于毕达哥拉斯三角形问题的页边空白处作注。注释①：方程x2+y2=z2有无限多组整数解。注释②：当n是大于2的正整数时，方程xn+yn=zn是没有正整数解的。费尔马并写道“我对此问题找到了奇妙的证明，可惜书的页边空白太窄了，写不下”。

注释①是关于勾股数的问题，早已被证明。注释②一般公认，当时不可能有正确的证明。此注释后来就称为费尔马大定理。

费尔马大定理挑战了人类近四百年。

1640年左右,费尔马运用无穷递降法已证明了n=4时，不定方程x4+y4=z4没有正整数解[2-3]。

1753年欧拉(Euler)证明了n=3时,费尔马大定理没有整数解。

1823年勒让德(Leqendre)证明了n=5时,费尔马大定理没有整数解。

1832年狄利克雷(Dirichlet)证明了n=14时,费尔马大定理没有整数解。

1839年勒贝格(Lebesgue)等证明了n=7时,费尔马大定理没有整数解。

从1621-1839年，历经数代数学家的努力，在这二百多年间只证明了费尔马大定理当n=3、4、5、7、14时的几种情形。直到1847年，凭借库木尔创立的“代数数论”这一现代工具，才证明了当n<100时的费尔马大定理，可认为是一次质的飞跃。

1900年，数学家希尔伯特在国际数学大会上把费尔马大定理证明列为23个数学难题之第十个问题。

1994年英国数学家安德鲁·怀尔斯用非初等的间接法攻克并证明了费尔马大定理。其历史性长文“模椭圆曲线和费尔马大定理”1995年5月发表在美国《数学年刊》第142卷，占满了整个全卷，共5章，130页。

2 费尔马大定理初等证明

2.1 分析

对任意1个正整数k，不定方程xn+yn=zn与xkn+ykn=zkn有无正整数解是等价的[4-6]。

若n有一个奇素数因子p， 则不定方程可变形为(xn/p)p+(yn/p)p=(zn/p)p。

而n=4时， 不定方程x4+y4=z4没有正整数解[3]， 如果n没有奇素数因子， 则p=2k,k≥2， 不定方程(xn/4)4+(yn/4)4=(zn/4)4。

因此，只需证明n为奇素数时，费尔马大定理成立即可。

2.2 证明

假设n为奇素数时，费尔马大定理成立。

令x=a,y=b,z=c为方程xn+yn=zn的1组正整数解，其中c是z的最小值，则

an+bn=cn

(1)

成立。

若(a,b)=d>1， 即d|a,d|b， 则d|c， 方程(1)变形为

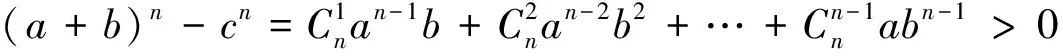
由(an-a)+(bn-b)=(cn-c)-(a+b-c)及费尔马小定理知

n|(an-a),n|(bn-b),n|(cn-c)

则

n|a+b-c

设a+b-c=mn， 由c>b>a， 则a-mn=c-b>0， 所以可设a=mn+e， 同理可设b=mn+f， 则c=mn+e+f， 其中m、e、f均为正整数。

则方程(1)变形为

(mn+e)n+(mn+f)n=(mn+e+f)n

(2)

按公式an-bn=(a-b)(an-1+an-2b+…+abn-2+bn-1)分解(2)式， 得

(mn+e)n=(mn+e+f)n-(mn+f)n=e[(mn+e+f)n-1+(mn+e+f)n-2(mn+f)+…+(mn+f)n-1]

同理得

(mn+f)n=(mn+e+f)n-(mn+e)n=f[(mn+e+f)n-1+(mn+e+f)n-2(mn+e)+…+(mn+e)n-1]

所以

e|(mn+e)n,f(mn+f)n

由于(a,b)=1， 所以(e,f)=1， 而

故

e|(mn)n,f|(mn)n

因此e、f中至多有1个含有因子n， 不妨设e含有因子n， 设e与mn的公共素数因子为n、p1、p2、…、pk，f与mn的公共素数因子为q1、q2、…、q1， 则

mn=Knα0p1α1p2α2…pkαkq1β1q2β2…q1β1，e=nλ0p1λ1p2λ2…pkλk，f=q1γ1q2γ2…q1γ1

其中αi,βj,λi,γj(i=0,1,2,…,k;j=1,2,…,l)都是正数。

则

λi≤nαi,γj≤nβj(i=0,1,2,…,k;j=1,2,…,l)

(3)

下面对(3)式中的不等式进行讨论。

情形1 在(3)式中至少有一个严格不等式成立的情形

在(3)式中，不妨设λ1

M=Knα0p2α2…pkαkq1β1q2β2…q1β1,N=nλ0p2λ2…pkλk， 则(2)式为

(Mp1α1+Np1λ1)n+(Mp1α1+f)n=(Mp1α1+Np1λ1+f)n

将上式利用二项式展开、移项、合并同类项、等式两端同除以p1λ1后，得

=0

依据整系数方程的整数根与常数项的关系，则p1|nNfn-1， 而(p1,f)=1, (p1,N)=1， 又p1与n是不同的素数， 有(p1,n)=1， 则上式矛盾， 从而假设λ1

同理可证λi

情形2 在(3)式中，如果λi=nαi,γj=nβj(i=1,2,…,k;j=1,2,…,l)

由于mn=Knα0p1α1p2α2…pkαkq1β1q2β2…q1β1， 则

e=nλ0p1λ1p2λ2…pkλk=nλ0p1nα1p2nα2…pknαk=nλ0(p1α1p2α2…pkαk)n

f=q1γ1q2γ2…q1γ1=q1nβ1q2nβ2…q1nβ1=(q1β1q2β2…q1β1)n

设p1α1p2α2…pkαk=T，q1β1q2β2…q1β1=S， 那么mn=Knα0TS,e=nλ0Tn,f=Sn，则(2)式为

(Knα0ST+nλ0Tn)n+(Knα0ST+Sn)n=(Knα0ST+nλ0Tn+Sn)n

按二项式展开、移项、整理得

+…+

+…+

+…+

等式两端同除以nλ0TnSn后，得

+…+

当α0=λ0=0时，

等式右端能被n整除， 而左端不能被n整除， 产生矛盾， 于是α0=λ0=0命题不成立。

当nα0-λ0=0时，

等式右端能被n整除， 而左端不能被n整除， 产生矛盾， 于是nα0=λ0不成立。

当nα0-λ0>1时，

等式左端能被n2整除， 而右端不能被n2整除， 产生矛盾， 于是nα0-λ0>1不成立。

同理可证则nαi-λi>1,nβj-γj>1(i=1,2,…,k;j=1,2,…,l)也不成立。

情形3 在(3)式中，假设λi=nαi,γj=nβj(i=0,1,2,…,k;j=1,2,…,l)

由于mn=Knα0p1α1p2α2…pkαkq1β1q2β2…q1β1，则

e=nλ0p1λ1p2λ2…pkλk=nnα0p1λ1p2nα2…pknαk=p1λ1(nα0p2α2…pkαk)n

f=q1γ1q2γ2…q1γ1=q1nβ1q2nβ2…q1nβ1=(q1β1q2β2…q1β1)n

设nα0p2α2…pkαk=T，q1β1q2β2…q1β1=S，那么mn=Kp1α1TS,e=p1λ1Tn,f=Sn，则(2)式为

(Kp1α1ST+p1λ1Tn)n+(Kp1α1ST+sn)n=(Kp1α1ST+p1λ1Tn+Sn)n

按二项式展开、移项、整理、等式两端同除以p1λ1TnSn后，得

+…+

+…+

等式右端能被n整除， 而左端不能被n整除， 产生矛盾， 于是nα1=λ1命题不成立。

同理可证λ1=nαi,γj=βj(i=1,2,…,k;j=1,2,…,l)命题不成立。

情形4 在(3)式中，λ0=0

把nα0并入K中，则(2)式为(KST+Tn)n+(KST+Sn)n=(KST+Tn+Sn)n

按an+bn=(a+b)(an-1-an-2b+…-abn-2+bn-1展开得

(2KST+Tn+Sn)[(KST+Tn)n-1-(KST+Tn)n-2(KST+Sn)

+…-(KST+Tn)(KST+Sn)n-2+(KST+Sn)n-1]

=(KST+Tn+Sn)n

则

2KST+Tn+Sn|(KST+Tn+Sn)n

所以2KST+Tn+Sn|(KST)n

因为(T,S)=1,[(T,S)=1,(K,S)=1,2KST+Tn+Sn>S,2KST+Tn+Sn>T)， 所以

2KST+Tn+Sn|Kn

令Kn=H(2KST+Tn+Sn)， 即

K(Kn-1-2HST)=H(Tn+Sn

(4)

则K、H必有公因子， 设(K,H)=d1， 存在2个正数n1,m1， 且(n1,m1)=1， 使得K=n1d1,H=m1d1， 则(4)式为

………………………

如此下去，由于m1≥m2≥m3≥…及mi(i=1,2,3,…)均为正数， 必进行有限步τ后mτ为1， 则(4)式为

K(kKn-τ-1-2ST)=Tn+Sn

Tn=K(kKn-τ-1-2ST)-Sn代入(KST+Tn)n+(KST+Sn)n=(KST+Tn+Sn)n得

[kKn-τ-(KST+Sn)]n+(KST+Sn)n=Kn(kKn-τ-1-ST)n

将[kKn-τ-(KST+Sn)]n展开，上式得

上式右端能被Kn整除，左端却不能，产生矛盾。

综上所述，费尔马大定理有正整数解的假设是不成立的。

[1]华罗庚.数论导引[M].北京：高等教育出版社，1957:318-319.

[2]闵嗣鹤，严士健.初等数论[M].北京：高等教育出版社，1998:34-35.

[3]潘承洞.初等数论[M].北京：北京大学出版社，2003:71-101.

[4]龚东山，刘岳巍，贾筱景.计算一类常微分方程特解的新方法[J].河北北方学院学报(自然科学版),2008,24(06):1-3.

[5]常秀芳，李高.关于伯努利方程的几种新解法[J].雁北师范学院学报,2007,23(02):89-91.

[6]李高，常秀芳.二阶变系数线性微分方程及其衍生方程[J].河北北方学院学报(自然科学版)，2011,27(05)：3-15.

[责任编辑：关金玉 英文编辑：刘彦哲]

Rudimentary Proof of Fermat’s Last Theorem

LI Gao

(School of Coal Engineering,Shanxi Datong University,Datong,Shanxi 037003,China)

Objective To explore the elementary proof of Fermat’s Last Theorem.Methods The binomial theorem expansion,the relationship between root and coefficient of algebraic equation,and the elementary number theory are adopted to prove Fermat’s Last Theorem with reduction to absurdity disproof and elementary method.Results For Fermat’s Last Theorem with any positive integern>2,indeterminate equationxn+yn=znhas no positive integer solutions.Conclusion The elementary method of Fermat’s Last Theorem can be used directly to prove the correctness of the conclusion,which abandons the cumbersome indirect elementary proof method and avoids the advanced higher solution.This provoking method gives the way of thinking and ideas to solve the problem in the study and application.

Diophantine equation;positive integer solution;common factor;odd prime;Fermat’s Little Theorem;Fermat’s Last Theorem

山西大同大学教学改革资金资助项目(XJY2013211)

李高(1965-)，男，山西天镇人, 副教授，研究方向：大学工科数学教育教学。

O 156.2

A

10.3969/j.issn.1673-1492.2017.07.001

来稿日期：2016-07-06