随机部分可积拟哈密顿系统的概率密度追踪控制*
2017-07-03朱晨烜柳扬丁云飞
朱晨烜 柳扬 丁云飞
(1.上海电机学院, 上海 200240) (2.上海航天第八设计部, 上海 201109)
随机部分可积拟哈密顿系统的概率密度追踪控制*
朱晨烜1†柳扬2丁云飞1
(1.上海电机学院, 上海 200240) (2.上海航天第八设计部, 上海 201109)
目前非线性随机系统的控制方法存在设计复杂, 计算成本高,以及缺乏稳定性或收敛性证明等缺点,针对这些问题,本文在作者前期研究的基础上发展了一种全新的针对部分可积的非线性随机系统的反馈控制, 使得受控系统输出的稳态概率密度逼近事先给定的目标概率密度, 并利用Lyapunov函数法证明受控系统的收敛性.数学仿真结果证明了这种方法的可行性和正确性.
等效非线性系统法, 随机反馈控制, Lyapunov函数法, 概率密度函数, 部分可积拟哈密顿系统
引言
物体运动、生物演化、工业过程、经济活动都不可避免会受到随机扰动,它们可以被看作是某些随机系统的输出过程.通常情况下会针对一些期望的目标设计随机系统的控制策略.因此,几十年来有关随机系统的目标追踪控制得到了广泛的发展.对于线性或线性化得到的系统,在高斯激励下输出仍为高斯过程,追踪控制目标为给定的期望和方差[1-4].而对于非高斯激励下的线性系统或任一激励下的非线性系统,其输出往往是非高斯的,仅以期望和方差作为控制目标是远远不够的.例如,以纤维的长度分布为控制对象的造纸工业以及工业锅炉中火焰的分布形态控制等等.
因此近十几年里,展开了以概率密度为控制目标的追踪控制研究,并逐渐成为随机系统控制领域的研究热点:Kreucher等提出了一种对多目标概率密度进行递归估算,从而追踪多个运动目标的方法[5];Guo和Yin在前期研究的基础上发展了一种鲁棒概率密度函数控制方法,针对具有建模误差和不确定性的时滞系统,使得系统输出的概率密度能够有效地追踪目标概率密度,并用前向的多步非线性累积成本函数来提高追踪性能[6];Yi等提出了一种基于两步神经网络的受迫的比例积分控制策略用于对目标概率密度的追踪控制[7];Pigeon等人设计了一类线性开关控制器用于一维系统的概率密度控制[8];Karny和他的合作者提出了一类系统完整概率控制设计方法[9,10].Annunziato和Brozi基于Fokker-Plank方程发展了一种多自由度随机系统以概率密度为目标的最优控制[11];Zhou等人设计了一种针对非高斯激励下的单自由度不确定随机系统的鲁棒追踪控制方法,使得系统输出概率密度与目标值的误差在给定时间内达到容许范围[12];针对多种外激共同作用下的具有分段线性刚度的单自由度系统,Yurchenko等人在动态规划与随机平均的基础上给出了系统概率密度控制的方法[13];Xing和Wu将概率密度控制方法应用到量子系统中[14];另外,将随机分布控制与迭代学习算法相结合,Yi和Sun等人给出了非高斯激励下单输出系统的最优追踪控制[15];Edward A. Buehler等人提出了一种以稳态概率密度为目标的非线性系统的模型预测控制[16];Wang和Qian应用了一种基于随机非线性系统FPK方程近似解的概率密度控制方法[17].
需要注意的是,上述控制方法多由数字优化计算得到,但这类方法对于分析闭环系统的稳定性和鲁棒性等存在很大的难度,因为数字优化过程中几乎不存在固定的闭环系统.
最理想的控制设计方法应该基于随机系统的精确解,但是就目前为止只得到了少部分的随机微分方程的精确平稳解[18-21].而如何利用现有的精确平稳解来解决控制律设计就成了关键问题.本文基于等效非线性系统法求解多自由度非线性随机近似平稳解的方法,发展了部分可积拟哈密顿系统以概率密度为目标的崭新的非线性随机最优控制方法.该法简单,能给出控制力的解析表达式,且能够证明系统最终必定逼近预定的概率密度.
1 部分可积拟哈密顿系统的等效非线性系统法
等效非线性系统法[19]是一种能保留非线性特性的求近似平稳解的解析方法.在高斯白噪声激励下多自由度耗散的哈密顿系统的等效非线性方法的基本思想是:给定一个得不到精确平稳解的非线性随机动力学系统,寻求一个既有精确平稳解的非线性随机动力学系统,又使得两系统之差在某种统计意义上最小.然后,以后者之精确平稳解作为前者之近似平稳解.

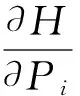
i,j=1,2,…,n;k=1,2,…,m
(1)
其中,Qi和Pi分别是广义位移和广义动量;Q=[Q1,Q2,…,Qn]T;P=[P1,P2,…,Pn]T;H=H(Q,P)是哈密顿函数;Mij(Q,P)是阻尼参数;σik(Q,P)是随机激励的强度;Bk(t) 是标准Wiener过程.
式(1)中Mij不满足存在精确平稳解的条件.其等效非线性随机动力学系统如下所示:
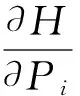
i,j=1,2,…,n;k=1,2,…,m
(2)
它具有与给定系统相同的哈密顿系统与随机激励,仅阻尼系数不同,它还具有精确平稳解.并有如下三种具有明确物理意义的等效准则:给定系统与等效系统阻尼力之差均方值最小;单位时间内给定系统与等效系统阻尼力耗能之差均方值最小;给定系统与等效系统的首次积分时间变化率期望相等.下面简要给出各种等效情况.(注意:本文中出现的大写字母表示随机过程或随机变量,小写字母表示确定的量.)
1.1 非共振情况
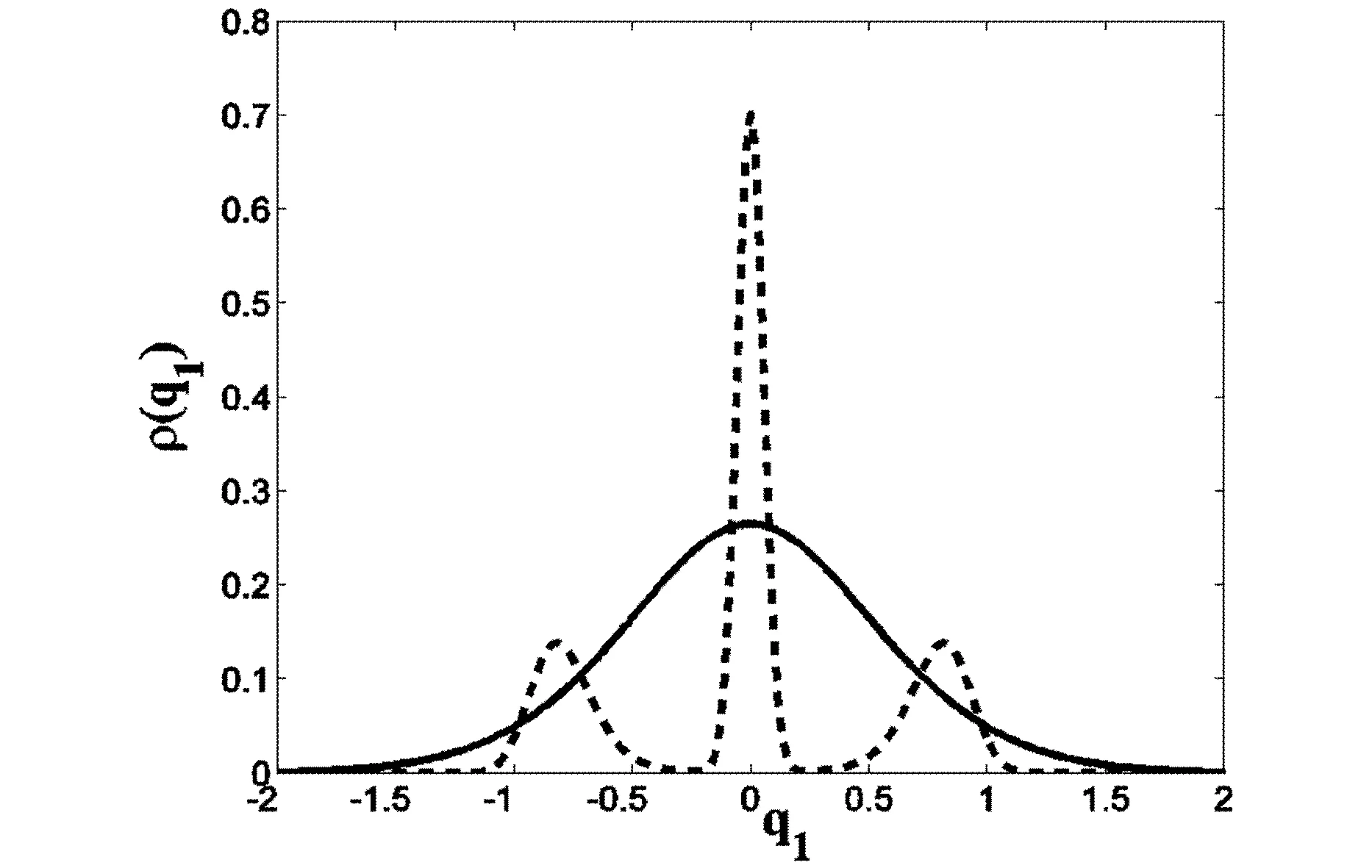
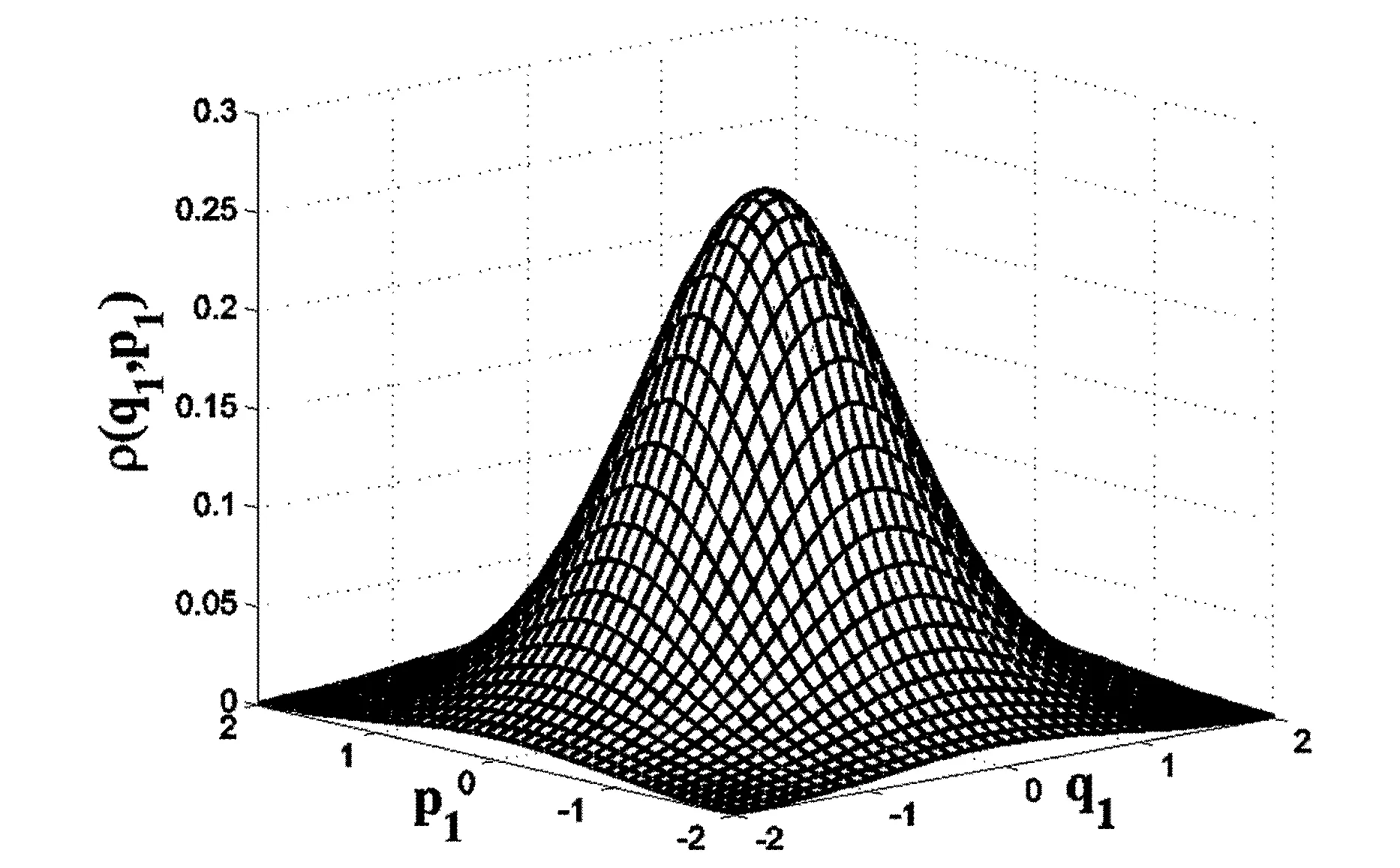
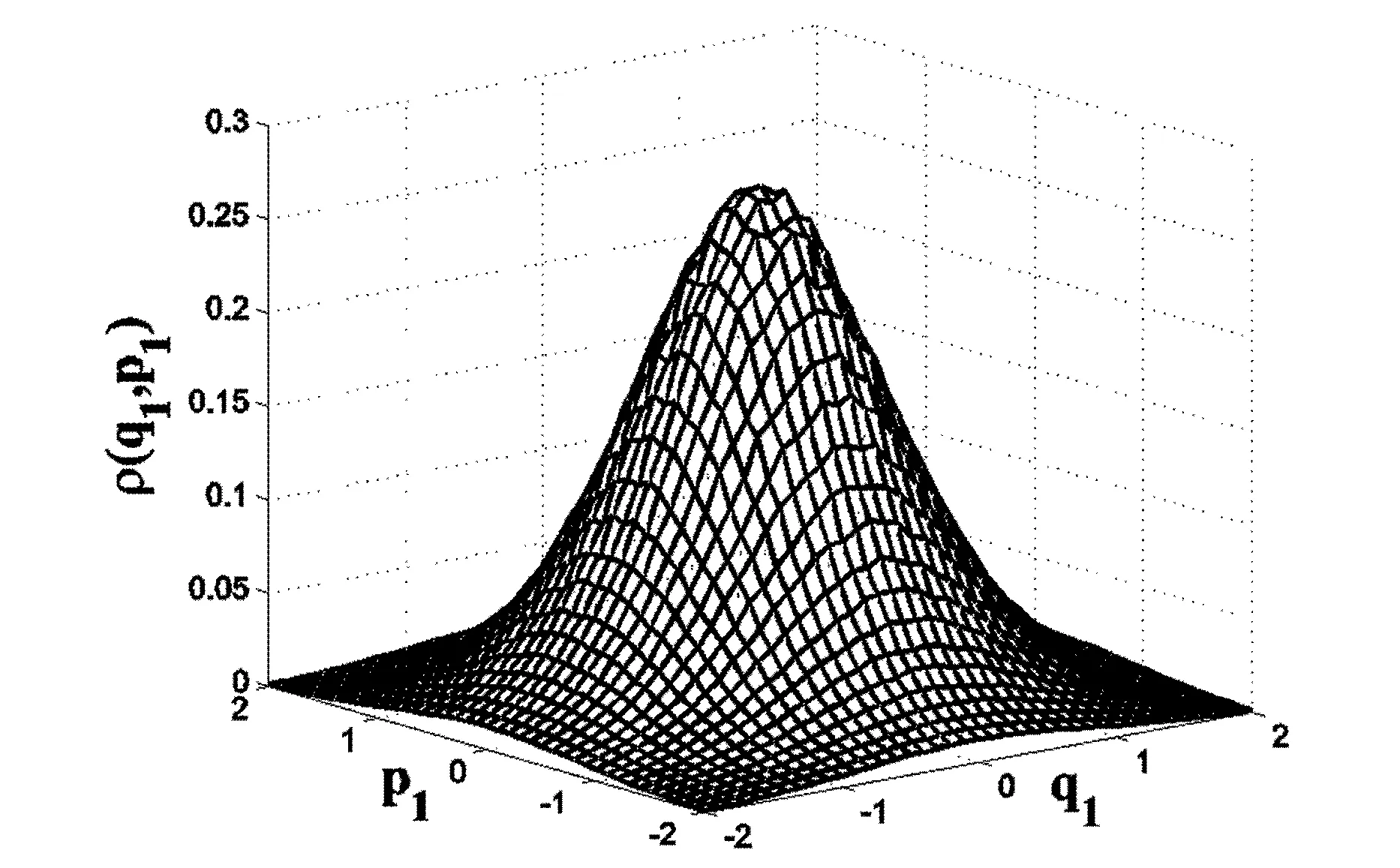
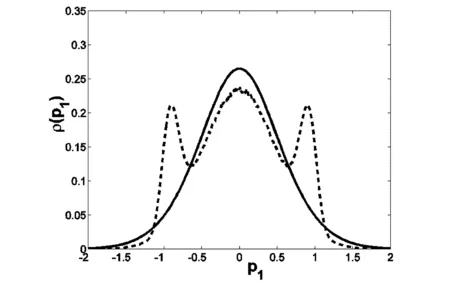
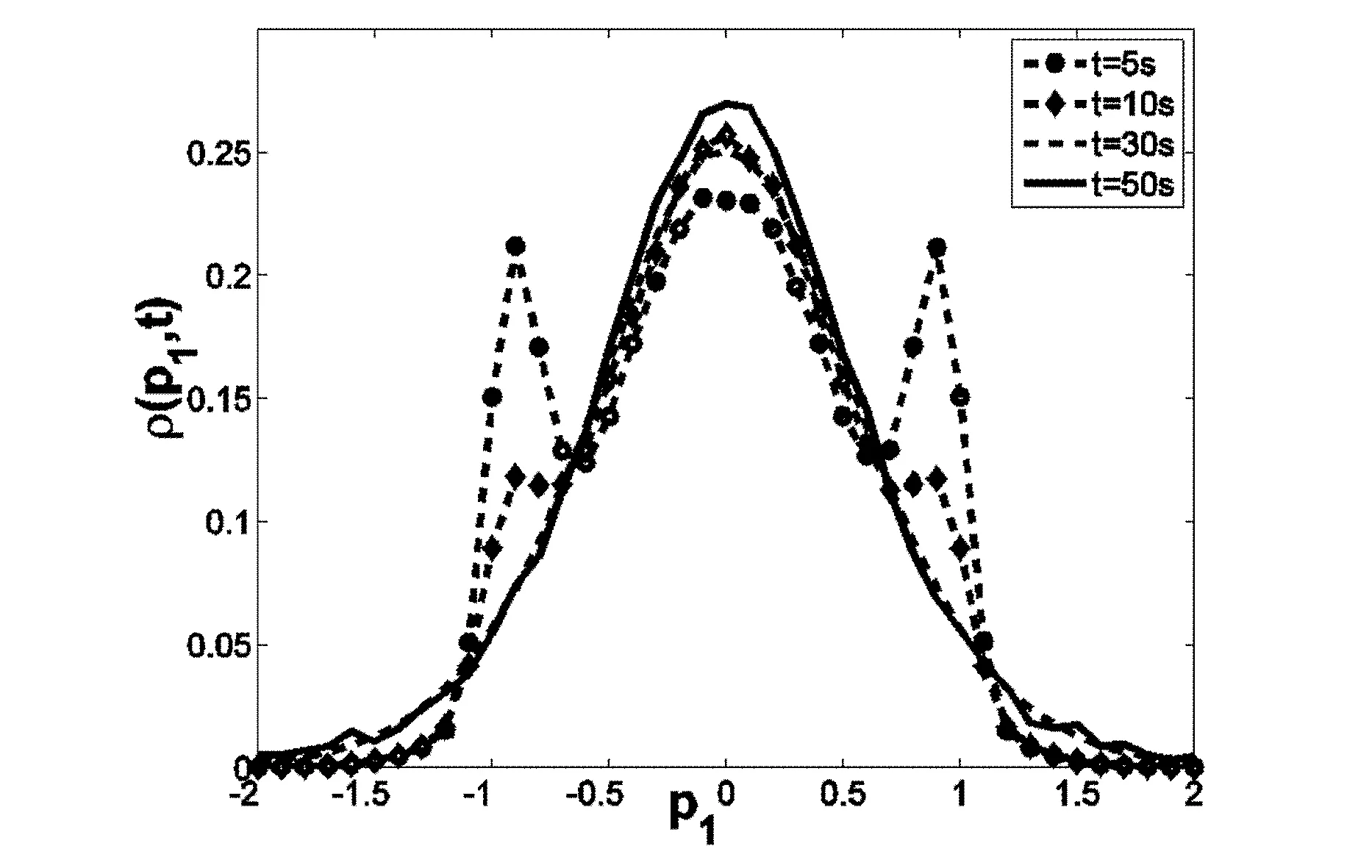
设与给定系统(1)相应的哈密顿系统为部分可积非共振, 已知r(1 s=1,2,…,r (3) 式中hs(H)=∂λ/∂Hs,等效系统与给定系统之差为: (4) 由上面提出的三种等效准则可以确定hs(H). 第一种等效准则的必要条件是: (5) 第二种等效准则的必要条件是: (6) 第三种等效准则的必要条件是: (7) 1.2 共振情况 设与给定系统(1)相应的哈密顿系统为部分可积共振,此系统存在β个内共振关系,引入角变量组合ψu,u=1,2,…,β. 此时,等效系统(2)具有如下的精确平稳解: η=1,2,…,r-1 (8) 式中,hη=∂λ∂Iη,hr=∂λ/∂Hr,hr+u=∂λ/∂ψu,等效系统与给定系统之差为: (9) 按照第一种等效准则,其必要条件如式(5);按第二种等效准则,其必要条件如式(6);按照第三种等效准则,其必要条件如式(7).其中s依次为η,r,r+u,共r+β个. 两种情况下的各种等效准则的具体求解过程可参看文献[21]. 2.1 设计过程 σik(Q,P)dBk(t) i,j=1,2,…,n;k=1,2,…,m (10) σik(Q,P)dBk(t) (11) 与上式相应的FPK方程为 (12) 假设目标概率密度为: ρ=Cexp[-φ(Q,P)] (13) (14) (15) 2.1.1 部分可积非共振 在非共振情况下, 目标概率密度满足如下形式: (16) 将式(16)代入式(12),可得到耗散控制力为: i,j=1,…,n;s=1,…,r (17) 2.1.2 部分可积共振 在共振情况下,目标概率密度满足如下形式: (18) 式中,Iη=Iη(qη,pη);Hr=Hr(qr,…,qn,pr,…,pn);ψu=ψu(q1,…,qr-1,p1,…,pr-1). 将式(18)代入式(12),可得到耗散控制力为: i,j=1,…,n;s=1,…,r-1;u=1,…,β (19) 2.2 输出过程的收敛性 引理1:对任一高斯白噪声激励系统: i=1,2,…,n (20) (21) 证明: 详见文献[22]. (22) (1)考虑非线性阻尼耦合的两个线性振子与一个两自由度非线性振子受高斯白噪声外激,其运动方程为: (23) 式中,αij为常数;ξk(t)是强度为2Dk的独立高斯白噪声. 与式(23)相应的Hamilton系统的Hamilton函数为: H=H1+H2+H3 (24) 系统(23)经转换,按存在精确平稳解的条件,其等效的受控非线性随机系统为 dQi=(∂H/∂Pi)dtdPi= -[∂H/∂Qi+(bij/2)hi(H)∂H/∂Pi+ui]dt+ σijdBi(t) bii=2Di,bij=0,i≠j,i,j=1,…,4 (25) 式中, (26) 设目标概率密度为: (27) 其中, (28) 显然,目标概率密度的指数部分是可积非共振的,由(15)式可以直接将未控哈密顿函数转化为与其相同的可积非共振形式. (29) 将式(27)与相应函数代入(17)式即可得到: (30) 按第一种等效准则,若满足条件: α13+α14=α15,α23+α24=α253(α33D3+α44D4)+α34D3+α43D4=2(α35D3+α45D4) (31) 可解得: (D3+D4) (32) 按第二种等效准则,若满足条件: α13+α14=α15,α23+α24=α255(α33D3+α44D4)+α34D3+α43D4=3(α35D3+α45D4) (33) 可解得: (34) 按第三种等效准则,若满足条件: α13+α14=α15,α23+α24=α25 3(α33D3+α44D4)+α34+α43=2(α35+α45) (35) 可解得: (36) 为了证明转移概率密度会随着时间逐渐逼近目标概率密度,引入如下李亚普诺夫函数: (37) V(q,p)的导数为: (38) 图1 未控系统的平稳概率密度(虚线)与受控系统的目标概率密度(实线)Fig. 1 PDFs of the uncontrolled system (dash) and the target value (solid) 图2 受控系统速度的概率密度随时间的变化过程Fig. 2 Evolution of ρ(q1,t) 图3 目标联合平稳概率密度(SPDF)Fig. 3 Target joint SPDF 图4 按一,三准则得到的受控系统联合概率密度Fig. 4 Joint SPDF under the first or third law 图5 按第二准则得到的受控系统联合概率密度Fig. 5 Joint SPDF under the second law (2)考虑给定系统(23)的共振情况,相应Hamilton系统存在内共振关系ω1=ω2,作用-角变量为I1,2=H1,2/ω1,2,θ1,2=arctan[p1,2/(ω1,2q1,2)], 引入角变量组合ψ=θ1-θ2.由式(9)可得给定系统与等效系统之差为: (39) 其中 M12=α16, M21=α26, (40) 按第一种准则,在条件(31)满足时,有: (α32D3+α42D4)ω2I2+(α35D3+α45D4)× (41) 按第二种准则,在条件(33)满足时,有: (α32D3+α42D4)ω2I2+(α35D3+α45D4)× (42) 按第三种准则,在条件(35)满足时,有: (α32D3+α42D4)ω2I2+(α35+α45)× (43) 李雅谱诺夫函数仍为(37)式所示,其导数同样为(38)式,因此满足收敛条件.图6为未控系统的平稳概率密度与受控系统的目标概率密度. 图7显示了受控系统转移概率密度ρ(p1,t)随时间变化的过程.可以看出随着时间的增加,转移概率密度ρ(p1,t)以阻尼力之差均方值最小(第一准则)或首次积分时间变化率期望相等(第三准则)或逼近目标概率密度ρ(p1). 从而验证控制力(29),(40)是非常有效的,不仅使系统输出逼近目标概率密度,而且满足一定意义上的误差最小.其中,ω1=ω2=1,其它参数均与例1中相同. 图6 未控系统的概率密度(虚线)与目标概率密度(实线)Fig. 6 PDFs of uncontrolled system (dash) and target value (solid) 图7 受控系统位移的概率密度随时间的变化过程Fig. 7 Evolution of ρ(p1,t) 本文发展了基于等效非线性系统方法的部分可积拟哈密顿系统输出概率密度的追踪控制,并且给出了输出过程的收敛性证明.与以往的控制方法相比,这一控制设计方法有设计过程简单,无需对瞬态转移概率密度进行实时监测,能够保证系统收敛等优点.该控制技术不但可以将非高斯输出转变为高斯输出,而且反之亦然.由于非线性随机系统在工程中的普遍存在性,这一控制技术具有非常重要的意义和广阔的应用前景.等效非线性系统法利用协方差等指标检验系统之间的“等价”能力.但对于非高斯激励的系统,方差等也不能作为衡量其接近程度的指标.因此我们今后的工作要进一步探讨非高斯激励下系统输出概率密度的追踪控制问题. 1 Aström K J, Wittenmark B. Self-tuning controllers based on pole-zero placement.IEEProceedings, 1980,127(3):120~130 2 Skelton R E, Iwasaki T, Grigoriadis K M. A unified algebraic approach to linear control design. Bristol, PA:Taylor & Francis, 1998 3 Lu J B, Skelton R R. Covariance control using closed-loop modelling for structures.EarthquakeEngineering&StructuralDynamics, 1998,27(11):1367~1383 4 Wojtkiewicz S F, Bergman L A. Moment specification algorithm for control of nonlinear systems driven by Gaussian white noise.NonlinearDynamics, 2001,24(1):17~30 5 Kreucher C, Kastella K, Alfred OH III. Multi-target tracking using the joint multi-target probability density.IEEETransactionsonAerospaceandElectronicSystems, 2005,41(4):1396~1414 6 Guo L, Yin L. Robust PDF control with guaranteed stability for non-linear stochastic systems under modeling errors.IETControlTheoryandApplications, 2009,3(5):575~582 7 Yi Y, Guo L, Wang H. Constrained PI tracking control for output probability distributions based on twostep neural networks.IEEETransactionsonCircuitsandSystemsPartI, 2009,56(7):1416~1426 8 Pigeon B, Perrier M, Srinivasan B. Shaping probability density functions using a switching linear controller.JournalofProcessControl, 2011,21(6):901~908 9 Herzallah R, Karny M. Fully probabilistic control design in an adaptive critic framework.NeuralNetworks, 2011,24(10):1128~1135 10 Karny M, Kroupa T. Axiomatization of fully probabilistic design.InformationSciences, 2012,186:105~113 11 Annunziato M, Brozi A. A Fokker-Plank control framework for multidimensional stochastic processes.JournalofComputationalandAppliedMathematics, 2013,237(1):487~507 12 Zhou J L ,Li G T, Wang H. Robust tracking controller design for non-Gaussian singular uncertainty stochastic distribution systems.Automatica, 2014,50(4):1296~1303 13 Yurchenko D, Iwankiewicz R, Alevras P. Control and dynamics of a SDOF system with piecewise linear stiffness and combined external excitations.ProbabilisticEngineeringMechanics, 2014,35(1):118~124 14 Xing Y F, Wu J. Probability density function control of quantum systems.InternationalJournalofModernPhysicsB, 2011,25(17):2289~2297 15 Yi Y, Sun C Y, Guo L. Probabilistic tracking control for non-Gaussian stochastic process using novel iterative learning algorithms.InternationalJournalofSystemsScience, 2013,44(7):1325~1332 16 Buehler E A, Paulson J A, Mesbah A. Lyapunov-based stochastic nonlinear model predictive control: Shaping the state probability density functions, In: Proceedings of the American Control Conference, Boston, To appear, 2016 17 Wang L Z, Qian F C. Technique of probability density function shape control for nonlinear stochastic systems.JournalofShanghaiJiaotongUniversity(Science), 2015,20(2):129~134 18 Caughey T K, Ma F. The steady-state response of a class of dynamical-systems to stochastic excitation.JournalofAppliedMechanics-TransactionsoftheASME, 1982,49:629~632 19 Lin Y K, Cai G Q. Exact stationary response solution for 2nd-Order nonlinear-systems under parametric and external white noise excitations.JournalofAppliedMechanicsTransactionsoftheASME, 1988,55(3):702~705 20 Zhu W Q. Exact solutions for stationary responses of several classes of nonlinear systems to parametric and (or) external white noise excitations.AppliedMathematicsandMechanics, 2012,38(2):197~205 21 Zhu W Q, Lei Y. Equivalent nonlinear system method for stochastically excited and dissipated integrable Hamiltonian systems.JournalofSound&Vibration, 2004,274(3-5):1110~1122 22 Caughey T K. Nonlinear theory of random vibrations.AdvancesinAppliedMechanics, 1971,11: 209~253 *The project supported by the National Natural Science Foundation of China under Grant(11302123), Innovation Program of Shanghai Municipal Education Commission under Grant(14YZ163) and “Chen Guang” project supported by Shanghai Municipal Education Commission and Shanghai Education Development Foundation under Grant(13CG63) † Corresponding author E-mail: zhucx@sdju.edu.cn 12 April 2016,revised 9 May 2016. TRACKING CONTROL FOR STATIONARY PROBABILITY DENSITY OF STOCHASTIC PARTIAL INTEGRABLE SYSTEM* Zhu Chenxuan1†Liu Yang2Ding Yunfei1 (1.ShanghaiDianjiUniversity,Shanghai200240,China) (2.The8thInstituteofShanghaiAcademyofSpaceflightTechnology,Shanghai200233,China) Current control methods for nonlinear stochastic system have the shortcomings such as complex design procedures, high costs, and lack of stability and convergence proof. Therefore, based on the equivalent nonlinear system method for obtaining the approximate stationary solutions of the nonlinear stochastic systems, this paper proposes an innovative design procedure for the feedback control of stochastic nonlinear system. The control aims at making the statistical information of the output steady-state probability density function (SPDF) follow those of a target SPDF. Moreover, Lyapunov function method is presented to verify the convergence of the controlled systems. Simulation results are also given to illustrate the feasibility and efficiency of this innovative design procedure. equivalent nonlinear system method, stochastic feedback control, Lyapunov function, probability density function (PDF), partial integrable system *国家自然科学基金资助项目(11302123),上海市教委科创项目(14YZ163),上海市“晨光计划”(13CG63) 10.6052/1672-6553-2016-039 2016-04-12收到第1稿,2016-05-09收到修改稿. † 通讯作者 E-mail: zhucx@sdju.edu.cn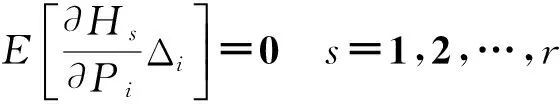
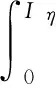
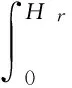

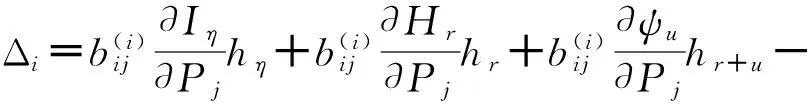
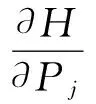
2 追踪控制设计
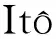
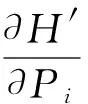
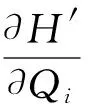
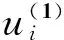
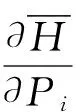

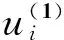
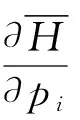
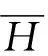
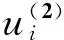




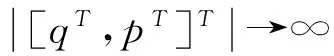
3 算例
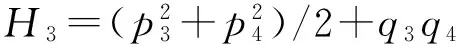


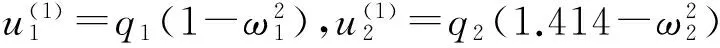
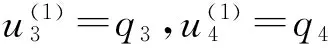

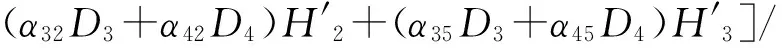
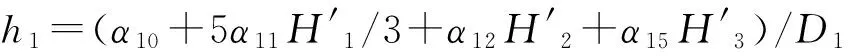
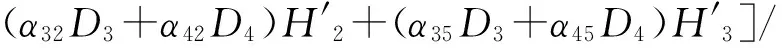
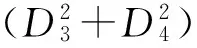

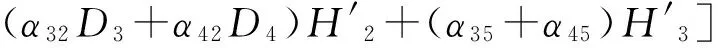



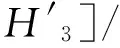



4 结论
