一种求解双障碍问题的迭代解法
2017-06-15马国春
马国春
(杭州师范大学理学院,浙江 杭州 310036)
一种求解双障碍问题的迭代解法
马国春
(杭州师范大学理学院,浙江 杭州 310036)
基于有限差分法,给出了一种求解双障碍问题的迭代方法,通过交替求解上障碍和下障碍两个子问题得到双障碍问题的近似解.迭代过程中,与上、下障碍的接触面积连续扩大并渐逼近问题的解.各子问题产生的迭代序列分别单调收敛.所构造的迭代方法全局收敛并有限步终止,数值实验显示该算法有较好的性能.
双障碍问题;有限差分法;迭代算法;非光滑牛顿法
0 前言


(1)

双障碍问题(1)可用于描述一张弹性膜在外力f作用且有两个障碍ψ和φ限制下的平衡位置u.
同时,双障碍问题现已被广泛应用于各种其他的物理问题中,诸如弹塑体的变形问题、Stefan问题、润滑问题等,更多应用可以参考文献[1-2].
众所周知,双障碍问题(1)的解可用第一类变分不等式[3-4]描述:求u∈K,使
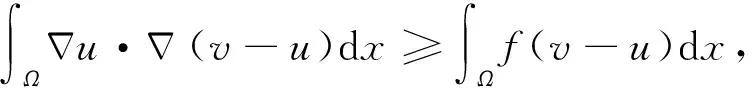
(2)
(3)
显然,Ω1(Ω2)是u与上(下)障碍相等区域.通常,Ω1和Ω2为接触区域,称Ω0为非接触区.显见,Ω=Ω0∪Ω1∪Ω2.由于此3个区域事先未知,也就是3个区域间的边界是未知的,故问题(3)亦被称为自由边界问题.(3)等价于
(4)
对于上述问题(1)~(4)或其经有限元法、有限差分方法离散后的系统求解工作,研究人员从各种角度,使用各种技术如优化技术[10-14]、并行计算技术[9,15]、多重网格或多水平集技术[4,6,12-14]、Howard算法[16]等展开过研究.本文采用有限差分法求解问题(3).对有限差分离散后的系统,该算法可以从任一初始点开始,交替求解两个上、下单障碍问题,其迭代产生的序列逼近离散系统的解,而每个上(下)单障碍子问题求解时产生的迭代序列分别都是单调下降(上升)并有限步终止,总算法全局收敛,且在n+1步迭代内终止,其中,n为所得离散系统的维度.
由于本文的子问题为单障碍问题,也有很多方法[10,17-21]可以采用.本文采用的求解方法来源于非光滑牛顿法[22]和一个特殊Jacobi选择方法[23-24]的结合.每个子问题的求解都是全局单调和有限步终止的,这就意味着本文的总算法是有限步终止的.数值实验进一步验证了该算法有较高的性能.
本文采用如下基本记号.|I|:集合I中的元素个数,Ai为矩阵A∈Rn×n中的第i个行向量,Ui为向量U∈Rn中的第i个分量.UT为一向量,其各分量是Ui,i∈T且T⊆{1,…,n}为一指标集,(A)ij表示矩阵A∈Rn×n中第i个行向量的第j个分量.AT,S是矩阵A=(aij)n×n中的|T|×|S|的子矩阵,其元素aij满足i∈T且j∈S,T,S⊆{1,…,n}为指标集.对于n×n矩阵A和B,A≥B表示(A)ij≥(B)ij,∀i,j=1,2,…,n.A≤B,A>B和A 将问题(3)经由5点差分格式离散后得到: (5) 将文[26]中对单障碍问题的结果推广,可以得到 UOSP:求U=(U1,U2,…,Un)T使得 (6) LOSP:求U=(U1,U2,…,Un)T使得 (7) 算法1(主算法) (8) 其中 (9) 这里, (10) 对于算法1,有 定理2 若U*是离散系统(5)的解,则 (11) 2)存在正整数Z (12) 成立,并且 (13) 分别为上下障碍的接触区域,也就意味着,算法1将在n+1迭代内终止. 上述定理表明,从任一初始点U(0)∈Rn出发,主算法1都是有定义的,且在有限步迭代内终止.因此,为求解离散系统(5),只剩下构造求解子问题UOSP和LOSP的算法了. (14) 由于子问题UOSP和LOSP都是单障碍问题,正如文[24]中所证明的,算法2和3在分别求解UOSP和LOSP时表现出较好的性能. 由文[24]中定理2,知 定理3 从任一初始点U0∈Rn出发,由算法2或3产生的迭代序列存在并分别单调收敛且有限步终止于式(6)和(7)各自的唯一解. 综合定理2与3,得到本文的主要结论: 定理4 从任一U(0)∈Rn为初始点出发,配以子算法2和3的主算法1总有定义,且在有限步内到达问题(5)的唯一解. (15) (16) (17) (18) (19) (20) 证明过程同定理1中1)的证明. 根据引理1和式(8)~(10),由数学归纳法,不难验证知如下引理2成立. (21) 3) 其中 (22) (23) 证明 由式(8)及引理2,知:∀k≥1, (24) (25) 进一步,根据文[24]中引理2,式(24)与(25)可分别导出 (26) (27) (28) 由上述式(27)与(28),结合文[24]中引理2,即得 (29) 式(26)与(29)可导出式(23).证毕. (30) (31) 对于k与l,若k≥Z≥l>0,据引理2,有 (32) 式(30),(31)和(32)表明U(k+2)即为系统(5)的解,也就是 U(k+2)=U*,∀k≥Z. (33) 同理可证, (34) 式(23),(33)与(34)将导出式(11)与(12)成立,从而有式(13).证毕. 定理4的证明 由定理3,也就是文[24]中的定理2,知子算法的每个迭代过程都是单调收敛且有限步终止的,再据定理2,主算法总是有定义且有限步终止,故定理成立.证毕. 数值实验1(弹塑体扭曲问题[14])Ω=(0,1)×(0,1),φ(x,y)=-dist((x,y),∂Ω),其中dist((x,y),∂Ω)表示点(x,y)与边∂Ω的距离,ψ(x,y)=0.2,S={(x,y)∈Ω||x-y|≤0.1且x≤0.3}, 表1所列为不同N下,外循环迭代步数与整个迭代过程中内循环所需要求解的线性方程组次数. 表1 不同N下的实验结果Tab. 1 Experimental results with different N 表2 迭代过程中所求线性方程组解的第1 985个分量数值Tab. 2 The value of the 1 985th component of the solutions generated during solving the linear equations in iterative processing 图1 数值解(N=64)Fig. 1 Numerical solution (N=64) 图2近似接触与非接触区(N=64)Fig. 2 Approximate contact and non-contact areas 图1为采用算法1所得近似解的三维图形.图2在坐标平面上分别以“*”和“°”标出了弹塑体与上下障碍接触区域,而“·"区为非接触区.表2则显示当N=64时,每个子算法求解线性方程组所得解第1 985个分量的值.这里,第1 985个网格点s1985的坐标正是(0.5,0.5). [1] FRIEDMAN A. Variational principles and free-boundary problems[M]. New York:Wiley,1982. [2] KINDERLEHRER D, STAMPACCHIA G. An introduction to variational inequalities and their applications[M]. New York: Academic Press Inc,1980. [3] XU X J, SHENG S M. Domain decomposition method for obstacle problem[J]. Numer Math J Chin Univ,1994,16(2):186-194. [4] ZHOU S Z, HU L H. Multigrid methods for bi-obstacle problems[J]. Hunan Ann Math,1991,11:20-30. [5] CIARLET P G. The finite element method for elliptic problems[M]. Amsterdam: North-Holland, 1978. [6] JIANG Y J, ZENG J P.L∞-error estimate for a discrete two-sided obstacle problem and multilevel projective algorithm[J]. Lobachevskii J Math,2006,24:43-53. [7] MERMRI B, CHEN X. On characterizations and regularity of the solution of bilateral obstacle problems[J]. Journal of Computational and Applied Mathematics,2003,152(1/2):333-345. [8] HUANG H C, WANG L H. The equivalence between a variational inequality and a differential form for obstacle problems[J]. Math Numer Sinica,1982,4:436-439. [9] ZENG J P, ZHOU S Z. On monotone and geometric convergence of schwarz methods for two-sided obstacle problems[J]. SIAM J Numer Anal,1998,35(2):600-616. [10] GLOWINSKI R. Numerical methods for nonlinear variational problems[M]. Berlin: Springer-Verlag,2008. [11] LI D H, ZENG J P. An iterative solution for two-sided obstacle problems[J]. J Numer Methods Comput Appl,1994,15:194-199. [12] HACKBUSCH W, MITTELMANN H D. On multi-grid methods for variational inequalities[J]. Numer Math,1983,42(1):65-76. [13] HOPPE R H W. Multigrid algorithms for variational inequalities[J]. SIAM J Numer Anal,1987,24(5):1046-1065. [15] ZHOU S Z, ZENG J P, ZHAN W P. Monotonic iterative algorithms for an implicit two-sided obstacle problem[J]. Comput Math Appl,2002,43(1/2):31-40. [16] BOKANOWSKI O, MAROSO S, ZIDANI H. Some convergence results for Howard’s algorithm[J]. SIAM J Numer Anal,2009,47(4):3001-3026. [18] HINTERMÜLLER M, ITO K, KUNISCH K. The primal-dual active set strategy as a semismooth newton method[J]. SIAM J Optim,2002,13(3):865-888. [19] TAI X C. Some new domain decomposition and multigrid methods for variational inequalities[C]//HERRERA I, KEYES D E, WIDLUND O B, et al. Fourteenth International Conference on Domain Decomposition Methods. Mexico: National Autonomous University of Mexico,2003:323-330. [20] XUE L. An algorithm for solving the obstacle problems[J]. Comput Math Appl,2004,48(10/11):1651-1657. [21] ZHANG Y M. Multilevel projection algorithm for solving obstacle problems[J]. Comput Math Appl,2001,41(12):1505-1513. [22] QI L Q, SUN J. A nonsmooth version of Newton’s method[J]. Math Program,1993,58(1):353-367. [23] HUANG Z D, MA G C. On the computation of an element of clarke generalized jacobian for a vector-valued max function[J]. Nonlinear Anal: TMA,2010,72(2):998-1009. [24] MA G C. A nonsmooth iterative algorithm for solving obstacle problems[J]. Journal of Hangzhou Normal University(Natural Science Edition),2012,11(4):295-301. [25] HACKBUSCH W. Elliptic differential equations: theory and numerical treatment[M]. Berlin: Springer-Verlag,1992. [26] CHENG X L, XUE L. On the error estimate of finite difference method for the obstacle problem[J]. Appl Math Comput,2006,183(1):416-422. max{u-ψ,min{-Δu-f,u-φ}}=0. An Iterative Algorithm for the Double Obstacles Problem MA Guochun (School of Science, Hangzhou Normal University, Hangzhou 310036, China) An iterative algorithm for solving the double obstacles problem is proposed basing on the finite difference method, which obtains the approximate solution by solving 2 subproblems including a locally upper obstacle subproblem and a locally lower obstacle subproblem alternately. In the iterative process, the solution is approximated by enlarging the contact regions of the upper and lower obstacle successively. The iterative sequences generated by each subproblem are monotonic convergent respectively. The iterative method proposed is convergent globally and stops in a finite number of iterations. Numerical experiments show that the algorithm puts up a good performance. double obstacles problem; finite difference method; iterative algorithm; nonsmooth Newton method 10.3969/j.issn.1674-232X.2017.03.016 2016-10-17 浙江省教育厅科研项目(Y201326696). 马国春(1973—),男,副教授,博士,主要从事数值优化与算法分析研究.E-mail:maguochun@163.com O241.5 MSC2010: 65K10;65N06;65F10;90C33 A 1674-232X(2017)03-0313-081 离散格式,误差估计及算法



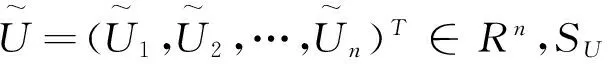
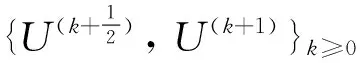




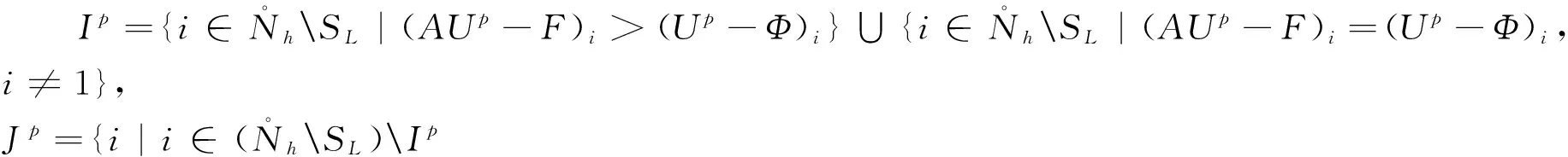
2 证明




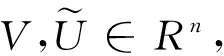




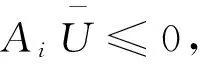
















3 数值实验






