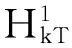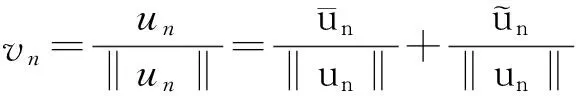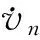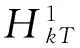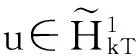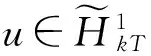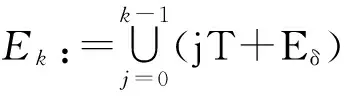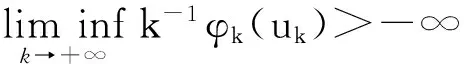一类二阶Hamilton系统次调和解的存在性
2017-06-05万树园王智勇
万树园,王智勇
(南京信息工程大学 数学与统计学院,江苏 南京 210044)
一类二阶Hamilton系统次调和解的存在性
万树园,王智勇*
(南京信息工程大学 数学与统计学院,江苏 南京 210044)
研究了一类次二次的二阶Hamilton系统次调和解的存在性.利用鞍点定理,得到了一个新的存在性结果,推广和改进了以往文献中的相关结论.
次调和解; 次二次; 临界点; 鞍点定理
1 主要结果
考虑二阶系统
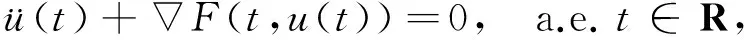
(1)
其中T>0,F:[0,T]×RN→R关于第一变量是T-周期的且满足以下假设:
(A) F(t,x)对每个x∈RN关于t是可测的,对a.e.t∈[0,T]关于x是连续可微的,且存在a∈C(R+,R+),b∈L1(0,T;R+)使得对所有x∈RN与a.e.t∈[0,T]有:
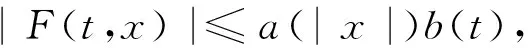
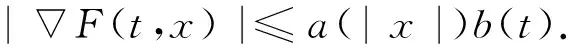
通常把kT-周期解称为次调和解.许多学者利用变分方法研究了问题(1)次调和解的存在性,并得到了一系列存在性和多解性结论,如文献[1-6].特别地,P.H.Rabinowitz[1]考虑了F(t,x)是次二次的情况并得到如下定理:
定理 A[1]若F∈C1(R×RN,R)且满足以下条件:
(F1) 存在常数1<μ<2,L1>0,使得对所有|x|≥L1,t∈[0,T]有
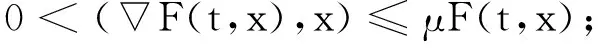
(F2) 存在常数a1,a2>0,1 定义 1.1 假设φ是这样的连续函数集合,对∀θ∈φ,存在常数M>0使得: (i) 对所有t∈R+,θ(t)>0; 最近,文献[7]通过引入控制函数θ∈φ,得到了一个新的次二次条件,并在此条件下研究了问题(1)周期解的存在性.受文献[1,3,7-9]的启发,本文利用文献[7]中新的次二次条件,考虑问题(1)的次调和解的存在性,给出本文的主要结论: 定理 1.2 若F满足假设(A)及以下条件: (H2) 当|x|→+∞时,F(t,x)≥0对a.e.t∈[0,T]一致成立; (H3) 存在子区间E⊆[0,T]满足meas(E)>0,使得对a.e.t∈E有 则问题(1)对每一个正整数k有kT-周期解uk,且满足当k→+∞时,‖uk‖∞→+∞. 注 1.3 显然定理1.2中的一系列假设都弱于定理A,因此结果显著推广了定理A.存在函数满足定理1.2但不满足文献[1,3-5,10-14]中的相关结果.例如:令 其中 设θ(|x|)=ln(2+|x|2)时,计算可知F(t,x)满足条件(H1)~(H3)但不满足(F1)与(F2). 注 1.4 因为F(t,x)关于t是T-周期的,不失一般性,可假设条件(A)中的b(t)是T-周期的. 则有 (2) 考虑能量泛函 由文献[1]易知,φk的临界点对应于问题(1)的kT-周期解. 为了证明定理1.2,需要如下结论. 引理 2.1[10]若F满足假设(A),E是[0,T]的一个可测子集,假设对a.e.t∈E有 则对∀δ>0,存在E的子集Eδ满足meas(EEδ)<δ使得 对所有的t∈Eδ一致成立. 引理 2.2[7]若F(t,x)满足假设(A)和(H1),则对所有x∈RN与a.e.t∈[0,T]有 其中 注 2.3 由θ的性质(ii),可知当|x|→+∞时,有G(|x|)→0;又依据1/θ的范围,有 因此t2G(t)关于t是递增的. 定义 3.1[15]设X是Banach空间,φk∈C1(X,RN),如果存在c∈R,{un}⊆X满足 称{un}为(C)c序列.如果对任意的c∈R,(C)c序列都有收敛的子列,我们称泛函φk满足Cerami条件(简称(C)条件). 引理 3.2 若假设条件(A)、(H1)、(H2)与(H3)成立,则能量泛函φk满足(C)条件. (3) 由假设(A)和(H1),对∀x∈RN与a.e.t∈[0,T]有 (4) 其中h2(t)=(2+M)h1(t)≥0.结合(3)和(4)式,对∀n∈N有 因此,存在常数M1>0使得 (5) 由(2)、(3)式和引理2.2、注2.3,对∀n∈N有 (6) 因此,当n→+∞时,有|un(t)|→∞对t∈[0,T]一致成立.由(H2)和(H3),有当n→∞时, (I2) ∀u∈RN,当|x|→+∞时,有φk(x+ek)→-∞. 结合注2.3可得(I1)成立. (7) 由ek(t)=k(cosωt/k)x0,则 由(H2)可知存在常数M1>0使得当|x|≥M1时有F(t,x)≥0.所以对∀x∈RN和a.e.t∈[0,T],有 (8) 因此利用(H2)和(7)、(8)式及注1.4,并注意到1/θ的范围,可知对所有|x|≥G+k,有 (9) 由β的任意性有当|x|→+∞时,φk(x+ek)→-∞.因此(I2)成立. 综上可知,存在临界点uk∈E使得 对x∈RN,令 由文献[4]可知,对所有充分大的k有 (10) (11) 对∀x∈RN和充分大的k,用与(9)式类似的方法,再结合(11)式并注意到θ的范围有 (12) 所以有 由β的任意性有 因此 (13) 最后,证明当k→+∞时,‖uk‖∞→+∞.假设结论不成立,则存在一个子列使得对所有k∈N有 其中C为一个正实数.因此,由条件(A)及注1.4有 [1] RABINOWITZ P H.On subharmonic solutions of Hamiltonian systems[J].Commun Pure Appl Math,1980,33(5):609-633. [2] LI C,Ou Z Q,Tang C L.Periodic and subharmonic solutions for a class of non-autonomous Hamiltonian systems[J].Nonlinear Analysis:TMA,2012,5(4):2262-2272. [3] TANG C L,WU X P.Subharmonic solutions for nonautonomous sublinear second order Hamiltonian systems[J].J Math Anal Appl,2005,304(1):383-393. [4] JIANG Q,TANG C L.Periodic and subharmonic solutions of a class of subquadratic second-order Hamiltonian systems[J].J Math Anal Appl,2007,328(1):380-389. [5] MAWHIN J,WILLEM M.Critical Point Theory and Hamiltonian Systems[M].New York:Springer-Verlag,1989. [6] RABINOWITZ P H.Minimax methods in critical point theory with applications to differential equations[C]//CBMS Regional Conference Series in Math,65.Providence RI:Am Math Soc,1986. [7] WANG Z,XIAO J.On periodic solutions of subquadratic second order non-autonomous Hamiltonian systems[J].Appl Math Lett,2015,40:72-77. [8] MENG F,ZHANG F.Periodic solutions for some second order systems[J].Nonlinear Analysis:TMA,2008,68(11):3388-3396. [9] TANG C L,WU X P.Notes on periodic solutions of subquadratic second order systems[J].J Math Anal Appl,2003,285(1):8-16. [10] TANG C L,WU X P.Periodic solutions for second order systems with not uniformly coercive potential[J].J Math Anal Appl,2001,259(2):386-397. [11] 居加敏,王智勇.一类带阻尼项的次二次二阶Hamilton系统的周期解[J].四川师范大学学报(自然科学版),2015,38(3):329-332. [12] 张鹏.一类次线性二阶Hamiltonian系统的无穷多周期解[J].四川师范大学学报(自然科学版),2010,33(5):588-591. [13] WANG Z,ZHANG J.Periodic solutions of a class of second order non-autonomous Hamiltonian systems[J].Nonlinear Analysis:TMA,2010,72(12):4480-4487 [14] HE X,WU X.Periodic solutions for a class of nonautonomous second order Hamiltonian systems[J].J Math Anal Appl,2008,341(2):1354-1364. [15] BARTOLO P,BENCI V,FORTUNATO D.Abstract critical point theorems and applications to some nonlinear problems with “strong” resonance at infinity[J].Nonlinear Analysis:TMA,1983,7(9):981-1012. 2010 MSC:34C25 (编辑 陶志宁) Subharmonic Solutions for a Class of Second-order Hamiltonian Systems WAN Shuyuan,WANG Zhiyong (SchoolofMathematicsandStatistics,NanjingUniversityofInformationScienceTechnology,Nanjing210044,Jiangsu) In this paper,we investigate the existence of subharmonic solutions for subquadratic second-order Hamiltonian systems.By using saddle point theorem,a new existence theorem is obtained.Our theorem extends and improves known results. subharmonic solution; subquadratic; critical point; saddle point theorem 2016-02-06 国家自然科学基金(11571176) O175.12 A 1001-8395(2017)02-0172-05 10.3969/j.issn.1001-8395.2017.02.005 *通信作者简介:王智勇(1979—),男,副教授,主要从事非线性泛函分析的研究,E-mail:mathswzhy@126.com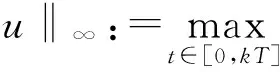
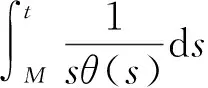
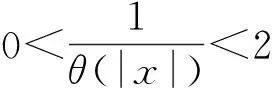
2 预备知识
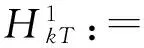
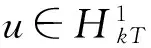
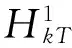
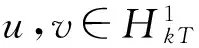
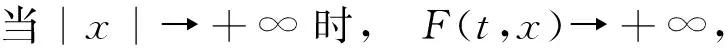
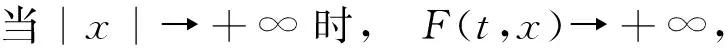
3 定理证明