The (G′/G)-expansion Method and Exact Solutions of Mixed KdV Equation

2017-05-15SHUJiZHANGJiaLIAOOu

四川师范大学学报（自然科学版） 2017年1期

SHU Ji, ZHANG Jia, LIAO Ou

(1. College of Mathematics and Software Science, Sichuan Normal University, Chengdu 610066, Sichuan;2. Department of Politics Education, Sichuan TOP IT Vocational Institute, Chengdu 611743, Sichuan)

SHU Ji1, ZHANG Jia2, LIAO Ou1

(1.CollegeofMathematicsandSoftwareScience,SichuanNormalUniversity,Chengdu610066,Sichuan;2.DepartmentofPoliticsEducation,SichuanTOPITVocationalInstitute,Chengdu611743,Sichuan)

In this paper, we discuss the travelling wave solution of the mixed (1+1)-dimensional KdV equation. By employing the (G′/G)-expansion method, we derive new exact travelling wave solutions of the equation, including hyperbolic function solutions, trigonometric function solutions and rational function solutions

nonlinear evolution equation; mixed (1+1)-dimensional KdV equation; (G′/G)-expansion method; exact travelling wave solution; solitary wave solution

1 Introduction

In the recent years, there has been growing interest in finding exact analytical solutions to nonlinear wave equations by using appropriate techniques, which can help one to well understand the mechanism of the complicated physical phenomena. The investigations of exact travelling wave solutions for nonlinear PDEs play an important role in the study of nonlinear physical phenomena. The nonlinear phenomena exists in all the fields including both the scientific and engineering fields such as fluid mechanics, plasma physics, optical fibers, biology, solid state physics, chemical kinematics, chemical physics, and so on. Many powerful methods have been established and developed to construct the travelling wave solutions of NLPDEs, such as the the tanh function method[1-4], Hirotas bilinear transformation[5-7],inverse scattering transform method[8], exp-function method[9-13],homogeneous balance method[14-15], the Jacobi elliptic function expansion method[16-18], sine-cosine method[19-20], the Backlund transform method[21]and so on. The above methods derived many types of solutions from most nonlinear evolution equations.

Every method has some restrictions in their implementations. Basically, there is no integrated method which could be utilized to handle all types of nonlinear PDEs. Another powerful and effective method has been presented by Wang et al.[22]to construct exact travelling wave solutions and is called the (G′/G)-expansion method. Afterwards, several researchers applied this basic method to obtain travelling wave solutions for different nonlinear PDEs[23-26]. In this paper, we consider the (1+1)-dimensional KdV equation

(1)

whereuis the function of (x,t),α0,α1,α2,βare nonzero constants. It has a broad background in hydrodynamics, plasma physics, gas dynamics. It is one of the equations which physicists and mathematicians are interested in [27]. Complexiton solutions to the Korteweg-de Vries equation[28], exact solutions of a KdV equation with variable coefficients[29], exact solutions of high-order KdV equations[30-32], new solitary wave for KdV-mKdV[33], soliton solutions for a generalized Hirota-Satsuma coupled KdV equation and a coupled MKdV equation[34-35], exact solutions of mixed Kdv equations[36-37]have been studied.

The aim of this paper is to construct the exact solutions of (1+1)-dimensional KdV Eq. (1). The paper is organized as follows. In Section 2, the procedure of (G′/G)-expansion method for finding the exact solutions to the nonlinear partial differential equation is introduced. In Section 3, hyperbolic function solutions, trigonometric function solutions and the rational function solutions are obtained. The conclusion is given in Section 4.

2 The (G′/G)-expansion method

Suppose the following NLPDEs in the form

(2)

whereu=u(x,t) is an unknown function,His a polynomial onu=u(x,t) and its partial derivatives, in which the highest order derivatives and nonlinear terms are involed. The essence of the (G′/G)-expansion method can be presented in the following steps:

Step 1 The travelling wave variable

(3)

reduces Eq.(2) to an ODE foru=u(ξ) in the form

(4)

whereCis a constant.

Step 2 Suppose that the solution of (4) can be expressed by a polynomial in (G′/G) as follows:

(5)

whereG=G(ξ) satisfies the second order linear differential equation in the form

(6)

whereai(i=0,1,…n) are constants to be determined later.

Step 3 Determine the positive integernin (5) by using the homogeneous balance between the highest order derivatives and nonlinear terms appearing in (4).

Step 4 Substituting (5) into (4) and using (6), collecting all terms with the same power of (G′/G) together, and then equating each coefficient of the resulted polynomial to zero, yields a set of algebraic equations forai,C,λandμ.

Step 5 Since the general solutions of (6) have been well known to us, then substitutingai(i=0,1),C,λ,μand the general solutions of (6) into (5) we have more travelling wave solutions of nonlinear partial differential (2).

3 Exact solutions of the mixed KdV equation

In this section, we apply the (G′/G)-expansion method to solve the mixed (1+1)-dimensional KdV equation.

We make the transformationu(x,t)=u(ξ),ξ=x+Ct. Then we get

(8)

where ′ denotes the derivative with respect toξ.

By integration with respect toξ, (8) becomes

(9)

whereDis the integration constant. We makeD=0.Balancingu‴ withu3givesN=1. Therefore, we can write the solution of (8) in the form

(10)

By (5) and (10) we derive

(11)

(12)

(13)

Substituting (10)-(13) into (9), setting the coefficients of (G′/G)i(i=0,1,2,3) to be zero, we obtain a system of algebraic equations fora0,a1,C,λandμas follows

(14)

(15)

(16)

(17)

We get

(18)

On solving the above algebraic equation set, we get

(19)

and

(20)

λandμare arbitrary constants. Substituting the solution set (19),(20) and the corresponding solutions of (6) into (10), we have three types of travelling wave solutions of the mixed KdV equations.

whenλ2-4μ>0, we obtain the hyperbolic function travelling wave solution

whereC1andC2are arbitrary constants of the general solutions of the second order linear ODE.

These are solitary wave solutions of the mixed KdV equation.

whenλ2-4μ=0, we obtain the rational function solutions

(25)

(26)

whereC1andC2are arbitrary constants of the general solutions of the second order linear ODE.

Whenλ2-4μ<0, we obtain the trigonometric solutions

(27)

(28)

whereC1andC2are arbitrary constants of the general solutions of the second order linear ODE.

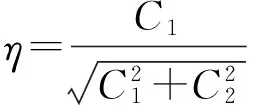
(29)

(30)

4 Conclusions

Inthispaper,the(G′/G)-expansionmethodisusedtoconductnewexacttravellingwavesolutionsofthenonlinearmixed(1+1)-dimensionalKdVequation.Asaresult,hyperbolicfunctionsolutions,trigonometricfunctionsolutionsandrationalfunctionsolutionswithparametersareobtained.Themethodisstraightforwardandconcise.Furthermore,theobtainedsolutionsimplythatthismethodisapromisingtoolbecauseitcangetmorenewtravellingwavesolutionswithfreeparameterofdistinctphysicalstructures.

[1] MALFLIET W. Solitary wave solutions of nonlinear wave equations[J]. Am J Phys,1992,60(7):650-654.

[2] PARKES E J, DUFFY B R. An automated tanh-function method for finding solitary wave solutions to nonlinear evolution equations[J]. Comput Phys Commun,1996,98(3):288-300.

[3] FAN E G. Extended tanh-function method and its applications to nonlinear equations[J]. Phys Lett,2004,A277(4/5):212-218.

[4] ABDOU M A. The extended tanh-method and its applications for solving nonlinear physical models[J]. Appl Math Comput,2007,190(1):988-996.

[5] HIROTA R. Exact envelope soliton solutions of a nonlinear wave equation[J]. J Math Phys,1973,14(7):805-810.

[6] HIROTA R, Satsuma J. Soliton solution of a coupled KdV equation[J]. Phys Lett,1981,A85(8/9):407-408.

[7] HIROTA R. Exact solutions of the KdV equation for multiple collisions of solutions[J]. Phys Rev Lett,1971,27(18):1192-1194.

[8] ABLOWITZ M J, CLARKSON P A. Nonlinear Evolution Equations and Inverse Scattering Transform[M]. Cambridge:Cambridge University Press,1991.

[9] HE J H, WU X H. Exp-function method for nonlinear wave equation[J]. Chaos Soliton Fract,2006,30(3):700-708.

[10] YUSUFOGLU E. New solitary for the MBBM equations using Exp-function method[J]. Phys Lett,2008,A372(4):442-446.

[11] ZHANG S. Application of Exp-function method to high-dimensional nonlinear evolution equation[J]. Chaos Solitions and Fractals,2008,38(1):270-276.

[12] BEKIR A. The exp-function for Ostrovsky equation[J]. Inter J Nonl Sci Num Simul,2009,10(6):735-740.

[13] BEKIR A. Application of the exp-function method for nonlinear differential-difference equations[J]. Appl Math Comput,2010,215(11):4049-4053.

[14] WANG M. Solitary wave solutions for variant Boussinesq equations[J]. Phys Lett,1995,A199(3/4):169-172.

[15] FAN E G, ZHANG H. A note on the homogeneous balance method[J]. Phys Lett,1998,A246(5):403-406.

[16] CHEN Y, WANG Q. Extended Jacobi elliptic function rational expansion method and abundant families of Jacobi elliptic function solutions to (1+1)-dimensional dispersive long wave equation[J]. Chaos,Solitons and Fractals,2005,24(3):745-757.

[17] LIU S, FU Z, LIU S, et al. Jacobi elliptic function expansion method and periodic wave solutions of nonlinear wave equations[J]. Phys Lett,2001,A289(1/2):69-74.

[18] LV D. Jacobi elliptic function solutions for two variant Boussinesq equations[J]. Chaos,Solitons and Fractals,2005,24(5):1373-1385.

[19] WANG M. Exact solutions of a compound KdV-Burgers equation[J]. Phys Lett,1996,A213(5/6):279-287.

[20] WAZWAZ A M. The tanh and the sine-cosine methods for the complex modified Kdv and the generalized Kdv equations[J]. Comput Math Appl,2005,49(7/8):1101-1112.

[21] ROGERS C, SHADWICK W F. Backlund Transformations[M]. New York:Academic Press,1982.

[22] WANG M, LI X Z, ZHANG J L. The (G′/G)-expansion method and travelling wave solutions of nonlinear evolutions in mathematical physics[J]. Phys Lett,2009,A372(4):417-423.

[23] ZHANG S, TONG J L, WANG W. A generalized (G′/G)-expansion method for the MKdV equation with variable coefficients[J]. Phys Lett,2008,A372(13):2254-2257.

[24] ZAYED E M, GEPREEL K A. Some applications of the (G′/G)-expansion method to nonlinear partial differential equations[J]. Appl Math Comput,2009,212(1):1-13.

[25] LI L, WANG M. The (G′/G)-expansion method and travelling wave solutions for a higher-order nonlinear Schrödinger equation[J]. Appl Math Comput,2009,208(2):440-445.

[26] FENG J, LI W, WAN Q. Using (G′/G)-expansion method to seek traveling wave solution of Kolmogorov-Petrovskii-Piskunov equation[J]. Appl Math Comput,2011,217(12):5860-5865.

[27] BOUNTIS T C. Singularities and Dynamical Systems[M]. New York:North-Holland,1985.

[28] MA W. Complexiton solutions to the Korteweg-de Vries equation[J]. Phys Lett,2002,A301(1/2):35-44.

[29] MA H, DENG A, WANG Y. Exact solution of a KdV equation with variable coefficients[J]. Comput Math Appl,2011,61(8):2278-2280.

[30] TRIKI H, WAZWAZ A M. Traveling wave solutions for fifth-order KdV type equations with time-dependent coefficients[J]. Commun Nonlinear Sci Numer Simulat,2014,19(3):404-408.

[31] GANJI D, ABDOLLAHZADEH M. Exact travelling solutions for the Lax’s seventh-order KdV equation by sech method and rational exp-function method[J]. Appl Math Comput,2008,206(1):438-444.

[32] GUO Z, KWAK C, KWON S. Rough solutions of the fifth-order KdV equations[J]. J Funct Anal,2013,265(11):2791-2829.

[33] TRIKI H, TAHA T R, WAZWAZ A M. Solitary wave solutions for a generalized KdV-mKdV equation with variable coefficients[J]. Math Comput Simul,2010,80(9):1867-1873.

[34] LI J, ZHANG Y. Solitary wave and chaotic behavior of traveling wave solutions for the coupled KdV equations[J]. Appl Math Comput,2011,218(5):1794-1797.

[35] FAN E G. Soliton solutions for a generalized Hirota-Satsuma coupled KdV equation and a coupled MKdV equation[J]. Phys Lett,2001,A282(1/2):18-22.

[36] 廖欧,舒级,曾群香. 一类混合KdV方程的精确孤立波解[J]. 四川师范大学学报(自然科学版),2015,38(4):493-496.

[37] 曾群香,黄欣,舒级,等. Wick-型混合随机KdV方程的精确解[J]. 四川师范大学学报(自然科学版),2015,38(1):27-33.

G′/G扩展法和混合KdV方程的精确解

舒级1, 张佳2, 廖欧1

(1. 四川师范大学数学与软件科学学院, 四川成都 610066; 2. 四川托普信息技术职业学院思政部, 四川成都 611743)

讨论一类混合1+1维KdV方程的行波解.通过运用G′/G扩展法,得到方程的一些新精确解,包括双曲函数解、三角函数解和有理函数解.

非线性发展方程; 混合1+1维KdV方程;G′/G扩展法; 精确行波解; 孤立波解

O175.29

1001-8395(2017)01-0055-06

2015-02-03

国家自然科学基金(11371267和11571245)和四川省科技厅应用基础计划基金(2016JY0204)