周后卿

(邵阳学院 理学与信息科学系，湖南 邵阳，422000)

关于Lyapunov矩阵方程的公共解

周后卿

(邵阳学院 理学与信息科学系，湖南 邵阳，422000)

设A,B是两个正则稳定的n阶实矩阵且A-B的秩为1。本文讨论了A,B的Lyapunov矩阵方程的公共解问题，给出了A,B的Lyapunov矩阵方程没有公共解的一个充分必要条件。

Lyapunov矩阵方程；公共解；充分必要条件

本文我们采用标准符号，用R表示实数集，用C表示复数集；用Mn(R)表示实数域上全体n×n阶矩阵的集合，Mn(C)表示复数域上全体n×n阶矩阵集合；用A*表示矩阵A的共轭转置矩阵，用I或In表示n×n单位矩阵，矩阵A的第(i,j)个元素记作Aij，矩阵A的秩记为rank(A)，矩阵A的迹记为tr(A)。对于矩阵P=P*∈Mn(C)，P>0(P≥0)表示P是一个正定(半正定)矩阵。对于矩阵P,Q∈Mn(C)，P>Q(P≥Q)意味P-Q>0(P-Q≥0)，也即P-Q是一个正定(半正定)矩阵；-P>0(-P≥0)意味着P<0(P≤0)。

一个矩阵A∈Mn(C)称作是稳定的，如果A的所有特征值的实部为负数，也即所有特征值都位于开的左半平面内。矩阵A是稳定的当且仅当存在一个矩阵P>0使得Lyapunov矩阵方程

AP+PA*=-Q<0，

(1)

则称P是矩阵A的Lyapunov方程的一个解。

本文在已有文献的基础上，讨论具有相同正则稳定矩阵的Lyapunov方程的公共解问题。

1 有关引理

矩阵A∈Mn(C)的惯性定义为三元整数组，记为In(A)=(i+(A),i-(A),i0(A))，这里i+(A)表示A的特征值中实部为正的个数,i-(A)表示A的特征值中实部为负的个数,i0(A)表示A的特征值中实部为零的个数。显然，对于n阶矩阵A，i+(A)+i-(A)+i0(A)=n；设A,B∈Mn(C)，用In(A)≤In(B)表示i+(A)≤i+(B),i-(A)≤i-(B)。若In(A)=(0,n,0)，则A为稳定矩阵；若In(A)=(n,0,0)，则称A为正稳定矩阵。

文献[4]证明了下列结论:设F∈{R,C}且A∈Mn(F)。则存在一个Hermitian矩阵P=P*∈Mn(F)，使得

PA+A*P<0

(2)

给定一个矩阵A，我们用Ρ(A)={P=P*∶AP+PA*<0}表示包含A的Lyapunov的所有解的集合。它的实数解集合用Ρr(A)=Ρ(A)∩Mn(R)表示。若P是关于A∈Mn(C)的Lyapunov方程的一个解，那么它也是关于A-1的Lyapunov方程的解。

为了证明本文的定理，需要下面几个引理。

引理1[5]若A,B是稳定的实矩阵且rank(A-B)=1。那么，A与B具有Lyapunov公共解的充分必要条件是矩阵AB没有一个负实特征值。

引理2[6]设矩阵A,B∈Mn(F)是正则稳定的且rank(A-B)=1，A与B没有Lyapunov公共解。那么，存在一个正整数r≤n和一个可逆矩阵T∈Mn(F)，使得

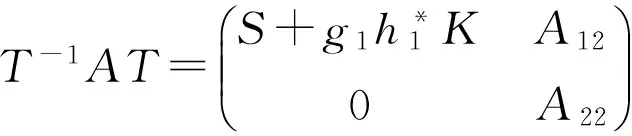
或者

这里，S∈Mr(F)是斜Hermitian矩阵(即S=-S*)，g1,h1∈Fr,g2∈Fn-r，A22,B22∈Mn-r(F)，K∈Mr(F)是一个秩为1的半正定矩阵且K≤Ir。

引理3[7]设矩阵Ai∈Mn(C)(i=1,2,…,k)，矩阵Ai没有Lyapunov公共解的充分必要条件是存在不全为零的半正定矩阵Hi(i=1,2,…,k)，使得

(3)

2 主要结论

现在开始证明本文的主要结论。

定理 设A,B是正则稳定n阶实矩阵且rank(U)=rank(A-B)=1。那么，A与B没有Lyapunov公共解的充分必要条件是矩阵AB有一个负实特征值。

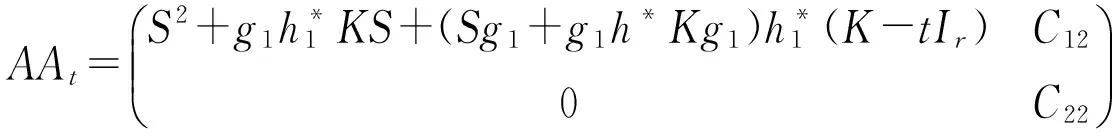
(4)

或

(5)

这里，C12∈Rr×(n-r)，C22∈Mn-r(R)。

(6)

(7)

(8)

考虑函数

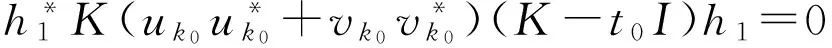
(9)

要么存在一个k0∈{1,2,…,s2}，使得对某些t0∈[0,1]，有

(10)

首先，对某些k0∈{1,2,…,s1}和t0∈[0,1]，假设(9)式成立，令

(11)

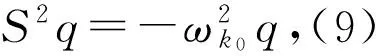
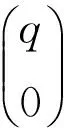
再则，对某些k0∈{1,2,…,s2}和t0∈[0,1]，假设(10)式成立，取q=wk0，则S2wk0=0

构造一个迹函数G(γ)=tr((A2+γI)-1AU)，这里γ≥0。现在我们要证明G(0)<1。

假设G(0)≥1，则

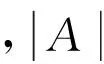
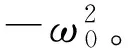
[1]Ito Y,Hattori S,Maeda H.On the decomposition of a matrix into the sum o f stable matrices [ J].Linear Algebra and its Applications,1999,(297):177-182.

[2]Wachspress E L.Trail to a Lyapunov equation solver[J].Computers & Mathematics with Applications,2008,55(8):1653-1659.

[3]Zoran Gajic and Muhammad Tahir Javed Qureshi.Lyapunov Matrix Equation in System Stability and Control[M].New York：Dover Publications,2008.

[4]Christopher King,Michael Nathanson.On the existence of a common quadratic Lyapunov function for a rank one difference[J].Linear Algebra and its Applications,2006,419:400-416

[5]Cohen N,Lewkowicz I.The Lyapunov order for real matrices[J].Linear Algebra and its Applications,2009,430(7):1849-1866.

[6]Cohen N,Lewkowicz I.Convex invertible cones and positive real analytic functions[J].Linear Algebra and its Applications,2007,425(2-3):797-813.

[7]Shorten R N,Narendra K S.On common quadratic Lyapunov functions for pairs of stable LTI systems whose system matrices are in companion form[J].IEEE Trans.Automat.Control,2003,48(4):618-621.

On common solutions for the Lyapunov matrix equations

ZHOU Houqing

(Department of Science and Information Science,Shaoyang University,Shaoyang 422000,China)

Let A and B be realn×nregularandstablematricessuchthatA-Bhasrankone.Inthispaper,wediscussedtheproblemthatAandBhaveacommonLyapunovsolution,andproposedanecessaryandsufficientconditiononthenon-existenceofacommonLyapunovsolutionforAandB.

Lyapunov matrix equation;common solution;necessary and sufficient condition

1672-7010(2017)01-0006-04

2016-07-1

湖南省教育厅科学研究项目(15C1235,16C1434);邵阳市科技局科技计划项目(2016ZD09)

周后卿(1963-),男,湖南新邵人,教授,硕士,研究方向:组合数学及其应用

O151.21 < class="emphasis_bold">文献标志码：A

A