王梅芳

[摘 要] 数学教材中有基本概念、基本定理，在解决问题中却需要在这基础上进行有效的总结，毕竟有效的总结能成为学生解决问题更好的武器，本文稱之为非教材性质. 如何运用非教材性质解决问题成为提高学生数学应试的一个新手段.

[关键词] 数学；非教材；性质；极化恒等式；向量共线；教材；仿射坐标系

众所周知，高中数学教材中有许多基本概念和基本性质、定理，是数学学习最基本的保障. 但是我们也发现，仅仅依赖这些基本公式和基本概念还是远远不够的，当下的数学应试考查了学生多方面的数学能力，这其中包括熟练运用知识解决问题. 如果从能取得更高分数的成绩、更快速的解决问题的角度来说，笔者认为除了教材中提及的基本知识之外，我们更需要一些从问题解决过程中总结下来的经验积累，这些积累可以浓缩成性质或特点，成为学生解题的“利器”.

非教材性质1：设O，A，B是不共线三点，对平面上任一点Q，有=x+y，则Q在直线AB上的充要条件是x+y=1.

此性质并非教材明确给出的概念或定理，只是在平面向量基本定理引入之后，在习题中涉及了类似的问题，我们将其提炼、总结成一条极为方便的判断共线的重要依据.从性质的使用来看，学生不善于发现性质隐藏于具体问题中的使用，另一方面也说明了来源于平面向量基本定理知识的不理解.

问题1：等差数列{an}满足=a1·+a100·且Q，A，B三点共线，则等差数列{an}前100项的和S100=________.

分析：本题改编自江西高考试题，属于非教材性质使用的第一层次，若学生能够准确领会三点共线的充要条件，本题属于难度系数较低问题，但是不少学生往往在问题中不能联系非教材性质、积累较少，导致问题的解决变得复杂.本题显然可知：a1+a100=1，所以S100=50.

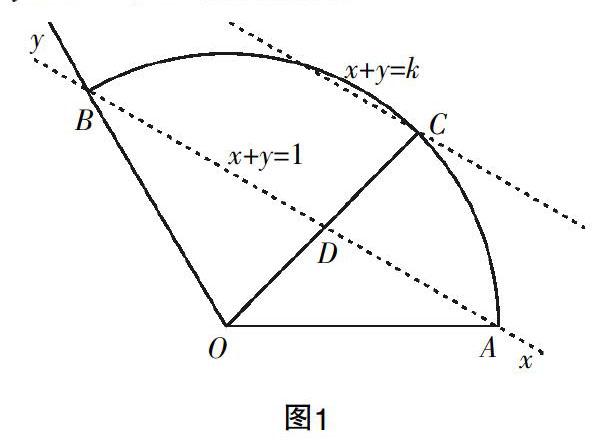
问题2：给定两个长度为1的平面向量和，它们的夹角为120°. 如图1所示，点C在以O为圆心的圆弧上变动. 若=x+y，其中x，y∈R，则x+y的最大值是________.

分析：本题是安徽省高考真题，笔者请学生尝试，大部分学生对于向量自由性的理解并不到位，均是利用直角坐标系正交分解状态下求解，这样的好处是思维简单，缺点是计算量较大，导致大部分学生最后在代数求解中无法求最大值.我们不妨换一个角度去思考问题，如图1所示，点C在圆弧上滑动，当其与点A或点B重合时，满足x+y=1，根据平面向量基本定理，我们不妨将OA记为x轴、OB记为y轴（此时根据向量自由性我们得到了一般化的仿射坐标系），在仿射坐标系里可以类似地如直角坐标系一般进行坐标化，根据比例可知，点C位于圆弧中点时，x+y有最大值，且显然最大值为2.

问题3：已知点A（1，-1），B（4，0），C（2，2），点P满足=λ+μ（1≤λ≤a，1≤μ≤b），若+=1，则点P（x，y）组成的平面区域的面积为________.

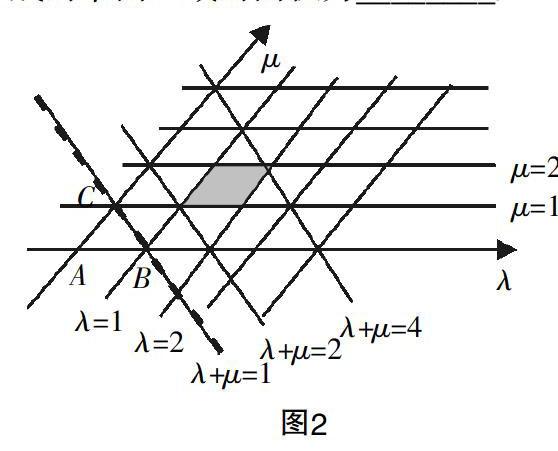
分析：考虑到+=1，我们不妨记a=2，b=2（其余同理），则1≤λ≤2，1≤μ≤2，当λ+μ=1时，由三点共线性质可知P，B，C共线，即点P位于BC上. 又由于1≤λ≤2，1≤μ≤2?2≤λ+μ≤4，因此点P所在区域由下列不等式组构成：1≤λ≤2，

1≤μ≤2，

2≤λ+μ≤4，即图2中所在阴影部分，其面积为△ABC面积的两倍.由条件易得该平行四边形的面积为8.我们发现，本题我们创造性地使用了三点共线性质，避免了直角坐标系带来的大量运算，从更为一般的仿射坐标系的角度解决了问题，性质使用的巧妙性凸显出来.

点评：我们发现，三点共线性质是依赖于平面向量基本定理存在的，其实平面向量基本定理是这一切存在的基础.不知道大家是否发现，我们在向量教学中往往对向量本质的知识关注并不多，更多的是关注了向量代数化的工具——运算，从利用坐标向量求解到空间向量解决立体几何，都是其代数化工具性的体现，但是向量是具备几何特性的，在平面向量基本定理所阐述的任意向量均可以使用基底进行唯一分解的情形下，向量的自由性得到了长足的运用，从而将一般化的仿射坐标系带来了美好的使用前景，给思维的开拓性带来了无限的可能. 本文列举了三个问题，每一问题都是层层递进式的设计，将知识的使用提炼到了更高的高度，从而获得了非教材性质的总结和积累.

非教材性质2：向量极化恒等式：a·b=.

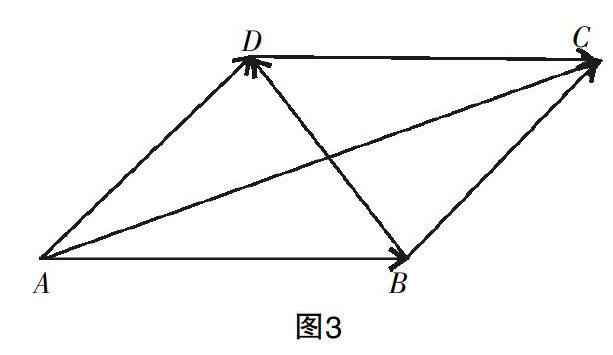
极化恒等式是向量数量积与向量和差之间的本质反映，但是教材中没有将这一重要的关系式作为数量积与向量和与差关系的性质进行总结. 笔者以为，能够为问题带来快捷的解决方式的重要特性都应该进行总结.那么极化恒等式到底在问题解决中如何使用？其揭示了什么？如图3所示，平行四边形ABCD中：=，=，=+，所以

2. 将①②相减即可得到向量极化恒等式，其沟通了向量内积运算与线性运算，成为非教材性质中重要的补充环节.

问题4：P是棱长为2的正方体上一动点，AB是正方体内切球的任意一条直径，则· 的取值范围是________.

分析：本题是研究向量数量积问题.从学生思维层面，第一选择是数量积的概念，但是我们很快发现·=

·

·cosθ，其中夹角θ很难在动态变换中找到其取值范围；第二选择是向量问题坐标化，这里高三的学生可以试一试，毕竟空间向量三维坐标运算是一种手段，但是不难发现运算量较大并不适合在考场中使用；因此第三选择极化恒等式成为问题解决的首选，考虑到·===2-1，我们发现只要解决

的取值范围即可，即研究正方体表面动点到正方体中心的距离最值，对于学生而言比较容易，显然1≤

≤，因此·∈[0，2]. 这里我们将数量积问题通过向量和与差转换为中线所在弦长以及对边所在长度问题，可见极化恒等式巧妙地绕开了向量内部的转换，揭示了问题处理的本质.

问题5：如图5，设△ABC中，P0是边AB上一定点，满足P0B=AB，且对于边AB上任一点P，恒有·≥·，则△ABC的形状是________.

分析：若直接使用第一思维数量积概念，我们不难发现向量的夹角难以计算；若采用直角坐标系进行运算，则明显由于三角形形状的任意性而必须构造特殊三角形才能为之；考虑到数量积与向量和与差之间的关系，取线段BC中点M，则4·=（+）2-（-）2=4

2-

2，要满足题意·最小，只需

最小即可，且最小位置恰为P0处. 很明显当且仅当MP⊥AB时满足题意，又M点为线段BC中点，所以AC=BC时成立，即原三角形为等腰三角形. 本题从极化恒等式的角度巧妙地化简了数量积问题，让学生开拓了解决数量积问题的非教材性质的使用. 通过两个问题的使用，我们发现非教材性质2在解决数量积与向量和与差之间关系有着极为重要的功效.

数学教学中还有一些非教材的性质，如数列中的等差数列通项公式与求和公式的函数观点下的表述；抽象函数关于轴对称g（a+x）=g（b-x）、中心对称g（a+x）+g（b-x）=c、周期性g（x+a）=g（x-b）等等三种表述式之间的研究、总结；立体几何中如何利用空间向量辨别二面角求解中的锐角或钝角；排列组合中插空法、捆绑法、隔板法等使用. 从本文所举的向量中非教材性质使用来看，教师教学要善于归纳、善于总结，对于教而言，没有很好的分门别类的梳理，教不可能成体系的进行；学生学习更需要这种系统化的指导，仅仅依赖教材的概念和公式，依赖学生自我发现在现阶段学生的能力和教学时间内是不可能做到的（所有非教材性质通过自主建构发现仅仅是理想主义）. 有了非教材性质，我们在解决问题的时候大大提高了知识使用的广阔性，对知识的理解也大大向前迈进.

总之，从专业化角度而言教师需要不断更新自己的知识体系，不断总结非教材性质，如文中仿射坐标系的引入、极化恒等式的总结给予教师自身对于数学知识的理解有了更高的层次.这些小小的性质使用为学生问题的解决带来了更为快捷、高效的手段，让知识真正在学生头脑中开枝散叶，为其解决难题树立更强的信心.