郑鹏飞, 刘 青, 赵菊娣, 林大钧, 安 琦

(1. 华东理工大学 机械与动力工程学院, 上海 200237; 2. 义乌工商职业技术学院, 浙江 义乌 322000)

一种任意曲线曲率中心、半径及Frenet标架的图解算法

郑鹏飞1, 2, 刘 青2, 赵菊娣1, 林大钧1, 安 琦1

(1. 华东理工大学 机械与动力工程学院, 上海 200237;
2. 义乌工商职业技术学院, 浙江 义乌 322000)

通过分析现有曲线曲率中心、曲率半径的求解方法, 与微分几何中Frenet标架的定义及求解方法, 提出了一种基于离散点分段构建平面曲线逼近空间任意曲线的方法， 并以此建立以两中垂面与密切平面求交的方式求解曲线曲率中心和Frenet标架的图解及解析模型. 所给出的求解任意曲线曲率中心、曲率半径及Frenet标架的图解算法简便可行, 试验证明，该算法稳定可靠, 适应性广.

曲率中心; 曲率半径; Frenet标架; 图解

在机械设计中, 经常涉及到复杂曲线的曲率半径和曲率中心的计算, 很多研究者提出了相应的计算方法[1-3], 如切线向量解法[4]、解析法[5-6]、施密特正交法[7]、图解法[8]、公式改进法[9]、复矢量法[10]、坐标变换法[11]等. 另外, 曲线曲率与Frenet标架在工程中有广泛的应用, 如车辆运行路线仿真、桥梁设计[12-16]等. 因此, 研究曲线曲率半径、曲率中心、Frenet标架问题在微分几何和工程应用领域均有重大现实意义. 虽然这些问题曾被广泛研究并应用, 但大多数研究局限于平面曲线, 或是将微分几何中已有的计算公式加以应用解决. 对于离散曲线或未知曲线方程情况下的曲率半径、曲率中心及Frenet标架求解问题的研究甚少. 本文针对这一问题, 提出了一种任意离散空间曲线曲率及Frenet标架求解算法.

1 曲线曲率及Frenet标架

设曲线C的方程为γ(s), 其中s为曲线的弧长参数, 则

(1)

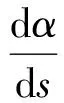
在正则曲线上曲率κ(s)不为零的点有一个完全确定的右手单位正交标架{r(s);α(s),β(s),γ(s)}, 它与表示曲线的笛卡尔直角坐标系的选取无关, 也不受曲线作保持定向的允许参数变换的影响, 称为曲线在该点的Frenet标架[17].

Frenet标架的3根轴分别称为曲线的切线、主法线和副法线; 3个坐标面分别称为曲线的法平面(以α为法向量的平面)、从切平面(以β为法向量的平面)和密切平面(以γ为法向量的平面), 它们的方程分别为

法平面: (X-r(s))·α(s)=0

(2)

从切平面: (X-r(s))·β(s)=0

(3)

密切平面: (X-r(s))·γ(s)=0

(4)

将曲线C的方程换成自然参数, 则曲线C方程为r=r(t), 对应的曲率及Frenet标架可表示为

(5)

(6)

(7)

(8)

2 曲线曲率及Frenet标架图解算法

Frenet标架由3个相互垂直的平面(法平面、从切平面、密切平面)组成, 3个平面的交线分别为主法线、副法线和切线, 其中主法线位于密切平面内. 根据密切平面的定义, 可以在曲线某点P1附近取两个点P2和P3, 分别连接直线P1P3、P1P2, 可得过直线P1P3中点A, 且以直线P1P3为法线的中垂面n1, 同理求得中垂面n2. 最后求得3个平面n1、n2、P1P2P3的交点P0, 即为曲线在P1点的曲率中心点. 如图1所示, 点P1和P0间的距离值即为曲率半径. 曲率半径的精度取决于P1附近点与P1的逼近程度, 即点P2和P3越逼近点P1, 曲率中心点的精度越高. 这一图解过程对于平面曲线, 其结果是显然的. 对于空间曲线, 这一图解模型同样适用, 因为空间三维曲线可看成离散的多段平面曲线依次连接而成. 换言之, 可将空间曲线离散化, 用一系列点将曲线离散表示, 这样具有避开求解复杂偏导数方程组的优点, 即适用于曲线方程未知的情况.

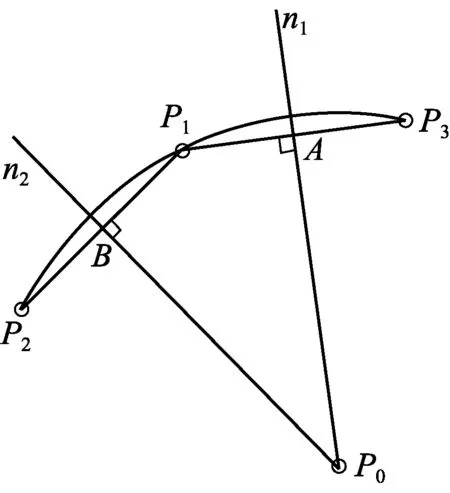
图1 曲率中心图解模型Fig.1 Graphical model of the curvature center

据此建立其数学模型, 已知点P1(x1, y1, z2), P2(x2, y2, z2)和P3(x3, y3, z3), 其平面的三点式方程为

(9)

平面n1的方程为

(10)

其中:A1=x3-x1=V2,B1=y3-y1=V4,C1=z3-z1=V6.

同理, 平面n2的方程为

(11)

其中:A2=x2-x1=V1,B2=y2-y1=V3,C2=z2-z1=V5.

为了简便起见, 令

联立式(9)～(11), 可得曲率中心点P0的坐标为

(12)

因此, 曲线C在点P1处的曲率半径R1=d(P0,P1), 曲率k1=1/d(P0,P1).

显然, 求得的曲率半径P0P1即为曲线在该点处的主法线. 副法线的向量即为平面P1P2P3的法向量γ, 而该向量在上述过程中已求得. 因此, 副法线即为过P0点, 并以γ为向量的直线. 同样, 切线即为过P0点, 并以主法线、副法线所在平面的法向量为向量的直线, 该直线较易得到, 在此不再赘述.

根据上述数学模型, 将其应用于求解离散空间曲线的曲率半径、曲率中心以及Frenet标架中， 可分为以下两类加以简述.

(1) 无显式曲线. 曲线用离散点表示, 可将该离散点组按就近原则将其排序, 使其满足连续化条件. 按其顺序, 依次取3点坐标, 即可根据上述模型计算出该离散曲线的Frenet标架.

(2) 显式曲线. 将曲线均匀分段, 并获取分段坐标值, 然后依次取点计算Frenet标架.

3 算例验证

为了进一步验证本图解算法的有效性和适用性, 本文通过3个实例加以验证. 利用AutoCAD软件中的vlax-curve-getFirstDeriv、vlax-curve-getSecondDeriv函数获得曲线的一次、二次偏导数, 再根据式(5)～(8)求解出曲线的曲率与Frenet标架, 以此作为验证的参照.

3.1 平面圆弧曲线

如图2(a)所示为一平面圆弧曲线, 测量该圆弧的半径可知为16.705 mm, 现将曲线均分为10段, 在每个分段点计算其Frenet标架与曲率半径. 图2(b)为利用本文算法与微分几何法求得的Frenet标架对比图, 本文算法计算出的曲率中心即为该圆弧圆心, 曲率半径也是16.705 mm, 精确率为100%. 图2(c)是图2(b)的局部放大图. 从图2(c)中可以看出, 本文算法标架与微分几何法标架完全吻合, 证明了本文算法对于求解平面曲线的Frenet标架、曲率中心、曲率半径是有效的.

(a) 任意圆弧线 (b) 本文算法与微分几何法所得标架图 (c) 标架放大图图2 平面曲线的Frenet标架求解过程Fig.2 Computing the Frenet frame of planar curve

3.2 圆锥面上测地线

图3(a)为点云圆锥面模型上的一条测地线, 图3(b)为用本文算法与微分几何法计算结果的叠加对比图. 由图3(b)可知, 本文算法同样适用于空间曲线的Frenet标架求解问题. 将图3(b)局部放大得到图3(c), 可见本文算法所得结果的精度很高.

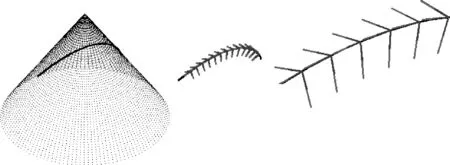
(a)圆锥面上一测地线 (b)本文算法与微分几何法所得标架图 (c) 标架放大图图3 圆锥面上测地线的Frenet标架求解过程Fig.3 Computing the Frenet frame of geodesic curve on conical surface

3.3 空间变径螺旋线

图4(a)为一变直径的空间螺旋线, 图4(b)为两种计算方法的运行对比结果. 从局部放大图4(c)可见, 本文算法与微分几何法计算结果有细小偏差. 分析该误差产生的原因可知, 由于在曲线上的取点密度(分段数)不同, 会造成Frenet标架计算误差, 因为曲线上三点取值间隔越大, 就会违反本文算法中三点共面, 用分段平面曲线逼近空间三维曲线的理论基础, 造成图4(c)中的偏移误差. 换言之, 取点间距越大, 误差越大, 间距越小, 精度越高. 因此, 利用本文算法计算Frenet标架、曲线曲率、曲率半径、曲率中心点坐标时, 需将取点间距设置成较小数值.

(a) 空间变径螺旋线 (b) 本文算法与微分几何法所得标架图 (c) 标架放大图图4 空间变径螺旋线的Frenet标架求解过程Fig.4 The solution process of Frenet frame on space variable helix

最后, 调整取点间距后, 针对平面曲线、空间测地线和空间变径螺旋线进行了多次重复试验, 试验结果表明本文算法对空间任意曲线的精度可达到99.9%, 可满足各种工程应用的需求, 具有实际应用价值.

3.4 曲线在Frenet标架上的投影

Frenet标架是用于描述欧几里得空间中的粒子在连续可微曲线上的运动, 它反映了曲线的切向、法向、副法方向之间的关系. 因此, 在获取曲面各点处的Frenet标架之后, 可将该曲线向Frenet标架的基本三平面作正投影, 得到3条平面曲线, 以此来描述原曲线某些特性. 据此, 本文中添加了该功能, 求得曲线上某点处基本三面形的平面方程, 然后将原曲线向这3个平面投影. 本文采用离散化的投影机理, 即将该曲线离散成坐标点, 将所有坐标点投影到平面上, 得到一系列相应的投影点, 最后将这一系列投影点光滑连接成曲线, 该曲线即为原曲线的正投影线. 离散化处理具有降维的优点, 能使问题简单化, 且能处理一些原本比较复杂的问题, 如本文中所提的曲线形式或方程未知及隐式曲线的曲率问题等. 图5为圆锥面测地线上9点分别向其基本三面形投影所得结果.

图5 圆锥面上测地线基本三面形投影图Fig.5 The basic three planes projection of the geodesic on conical surface

4 结 语

本文提出了一种完整的适用于平面、空间任意曲线曲率问题的求解模型, 并利用离散方法进行降维来处理曲线信息不确定的问题， 提出了图解方式解决图形问题, 避免求解复杂微分方程组的困境. 应用所建的算法, 对压力容器壁厚计算中涉及的曲面主曲率半径、轧辊机辊子疲劳强度计算涉及的曲面主曲率半径的求解都取得了直观、快速、准确的结果. 将曲线投影到Frenet标架上, 为直观地研究曲线特性提供了方法.

今后的研究工作将在以下几方面开展: 带噪声的离散曲线或隐性复杂曲线的Frenet标架求解; Frenet标架的机械工程领域的具体应用; 利用曲线曲率或Frenet进行给定条件的曲线、曲面设计等.

[1] REINOSO J F, MOMCAYO M, PASADAS M, et al. The Frenet frame beyond classical differential geometry: Application to cartographic generalization of roads [J]. Mathematics and Computers in Simulation, 2009, 79(12): 3556-3566.

[2] KULAHCI M, BEKTAS M, ERGUT M. On harmonic curvatures of a Frenet curve in Lorentzian space [J]. Chaos, Solitons and Fractals, 2009, 41(4): 1668-1675.

[3] ENCHEVA R P, GEORGIEV G H. Similar frenet curves [J]. Results in Mathematics, 2009(55): 359-372.

[4] 杨老记. 空间曲线的切线向量求法[J]. 邢台职业技术学院学报, 2003, 20(5): 26-28.

[5] 张学东. 空间曲线的曲率计算方法[J]. 塔里木农垦大学学报, 2002, 14(2): 10.

[6] 闫焱. 空间曲线的主法向量方向的探讨[J]. 陕西师范大学继续教育学报, 2005, 22(3): 104-105.

[7] 包图雅, 张陆. 曲线上的Frenet标架[J]. 湖北民族学院学报(自然科学版), 2015, 33(3): 245-247.

[8] 徐进. 任意复杂曲面曲线零件曲率半径的图解法[J]. 现代机械, 2003(4): 12-13.

[9] 冯书香, 潘虹. 微分几何中Frenet公式的新想法[J]. 牡丹江师范学院学报(自然科学版), 2012(1): 5-6.

[10] 王允地, 王良文. 用复矢量法建立机械设计中曲线曲率半径和曲率中心的统一计算式[J]. 陕西科技大学学报, 2009, 27(2): 108-115.

[11] 李崇虎. 用坐标变换法求曲线的曲率半径[J]. 西南师范大学学报(自然科学版), 2006, 31(1): 180-183.

[12] 周啟, 张昭. 带式输送机曲线段曲率半径的计算研究[J]. 矿山机械, 2013, 41(5): 70-72.

[13] 潘登, 郑应平. 路径约束条件下车辆行为的时空演化模型[J]. 物理学报, 2015, 64(7): 078902, 1-6.

[14] 付朝晖, 郁玮, 崔思明. 一种基于 Frenet 标架的声线计算新方法[J]. 声学与电子工程, 2013(3): 26-29.

[15] 刘立民. 曲率半径对曲线矮塔斜拉桥的影响分析[J]. 公路交通科技(应用技术版), 2015(5): 153-155.

[16] 黄新艺, 陈彦江, 李岩，等. 曲率半径对曲线箱梁桥车辆荷载作用下冲击效应的影响[J]. 振动与冲击, 2010, 29(1): 38-41.

[17] 梅向明, 黄敬之. 微分几何[M]. 4版. 北京：高等教育出版社, 2008: 13-50.

A Graphical Algorithm for Computing the Center, Radius of Curvature and Frenet Frame on Any Curves

ZHENGPeng-fei1, 2,LIUQing2,ZHAOJu-di1,LINDa-jun1,AnQi1

(1. School of Mechanical and Power Engineering, East China University of Science and Technology, Shanghai 200237, China; 2. Yiwu Industrial & Commercial College, Yiwu 322000, China)

A method of approximating space curve based on planar curves constructed by discrete points is proposed through analyzing the existing methods of computing the curvature center and curvature radius of curves and the definition and solving method of Frenet frame in differential geometry. A graphical model and mathematical model for computing the curvature center of the curve and Frenet frame are constructed by computing the intersection of two vertical planes and osculating plane. The graphical computing algorithm for computing the curvature center of curves and Frenet frame presented is simple and feasible. It is proved that this algorithm is stable and reliable, and the adaptability of this algorithm is extensive.

curvature center; curvature radius; Frenet frame; graphics

2015-12-20

浙江省教育厅科研资助项目(Y201432394)

郑鹏飞(1984—)，男，浙江兰溪人，讲师，博士研究生，研究方向为CAD&CAGD、反求工程.E-mail：pfzheng@126.com

TP 391

A