王新奇

(西安文理学院 学报编辑部，西安 710065)

不可约非负矩阵研究

王新奇

(西安文理学院 学报编辑部，西安 710065)

介绍非负矩阵与不可约非负矩阵的概念，探讨不可约非负矩阵的结构，并得到了一些很有用的结果，这些结果是一般矩阵所不具备的.

正矩阵；非负矩阵；不可约非负矩阵

非负矩阵是在计算机科学、经济数学、概率论以及系统稳定性分析等领域经常会遇到的一类特殊矩阵，这些矩阵的元素都是非负的.关于不可约非负矩阵的结构也有一些很有用的结果，这是一般矩阵所不具备的.

1 正矩阵与非负矩阵

定义1 设A=(aij),B=(bij)∈Rm×n，如果对所有的i,j都有aij≥bij,则记为A≥B.如果对所有的i,j都有aij>bij,则记为A>B.特别的，如果A≥0,则称A为非负矩阵.如果A>0,则称A为正矩阵.

定理1(正矩阵的Perron定理) 设A∈Rn×n为正矩阵，并且ρ(A)为其谱半径，则

(1) ρ(A)为A的正特征值，它对应着一个正的特征向量；

(3) ρ(A)为A的单特征值.

注 正矩阵只是不可约非负矩阵的一种特殊情形，正矩阵的Perron定理不能全部照搬到非负矩阵上.

2 不可约非负矩阵

对于任意非负矩阵，有以下引理.

引理1[1]设A是n阶非负矩阵，则谱半径ρ(A)是A的特征值，并且存在非负向量x≥0,x≠0使得Ax=ρ(A)x.

证明 设∀t>0,可以令At=(aij+t)>0,用x(t)代表At的Perron向量，满足

由子列极限定理可知t→0时{x(t)}一定有收敛子列，即可得出结论.

一个方阵P，如果它的每一行和每一列都只有一个元素为1，其余的元素都为零，则矩阵P称为一个置换矩阵.显然P可通过交换单位矩阵I的行或列而得到，这种矩阵是正交阵(P-1=PT).交换矩阵的两行(或两列)，可用左乘(或右乘)一个适当的置换矩阵P来实现.

定义2[2]n阶矩阵A称为可约的，如果满足下列条件之一：

(1)n=1并且A=0；

(2)n≥2,存在n阶置换矩阵P，使得

其中，B是k阶矩阵，1≤k≤n-1,左下角是(n-k)×k的零阵.否则就称A为不可约的.

推论1 (1)正矩阵是不可约的；(2)不可约矩阵都是非零矩阵；(3)A为不可约，当且仅当AT为不可约.

注 只要通过一系列交换矩阵的行与列，可在指定的左下角位置得到一个(n-k)×k的零子块，则A为可约的.由定义2可知，如果A为可约，则其至少有(n-1)个0元.

定义3 一个n阶矩阵A，如果可以将下标集{1,2,…,n)}划分为非空不交集合I1和I2，使得当i∈I1,j∈I2时，aij=0，则称其为可约的.否则，A称为不可约的.

3 主要结果

利用定义判别矩阵是否可约是困难的，下面给出一个非负矩阵是否可约的判定条件.

引理2[3]n阶非负矩阵A为不可约的充要条件是(I+A)n-1>0.由此可知，A为不可约的，当且仅当AT为不可约.

证明 充分性.当(I+A)n-1>0.时，如果A为可约矩阵，则存在置换矩阵P，使得

有

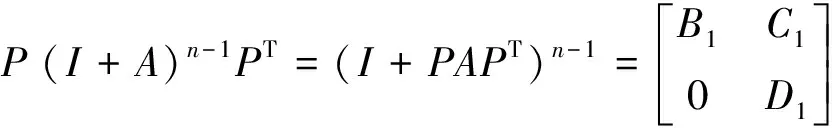
于是P(I+A)n-1PT有零元，从而(I+A)n-1有零元，与条件相矛盾.

必要性.由于A是不可约矩阵，只需证明对任意非零向量x≥0,x≠0都有(I+A)n-1x>0即可.先证明在条件x≥0,x≠0下，x中零元个数一定大于y=(I+A)x中零元个数.假若相反，因为y-x=Ax≥0,y≥x,所以如果y的第i个坐标为0，则x的第i个坐标也为0，这样y的0元个数不会多于x的0元个数，即x与y有相同的0元个数.

所以不失一般性(利用行置换)，有

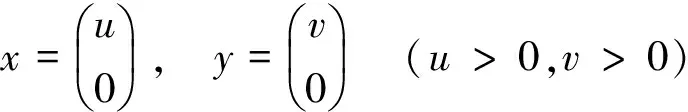
这里的向量u,v有相同的维数.再令

则y=(I+A)x变为

由此可得A21u=0,又因为u>0,故有A21=0,这与A不可约是相矛盾的.因而x与y不可能有相同的0元个数.从而也就证明了x的0元个数多于y的0元个数，即(I+A)x的正坐标个数多于x的正坐标个数.

上述结果表明：x每用I+A左乘一次，其正坐标的个数都会增加，因此(I+A)2x的正坐标个数多于(I+A)x的正坐标个数.由此可知(I+A)2x至少比x多两个正坐标，(I+A)n-1x至少比x多n-1个正坐标，但x≠0,x至少有一个正坐标，所以(I+A)n-1x至少有n个正坐标，即(I+A)n-1x>0.

证明 充分性可由反证法与可约定义得到.下面证明必要性.

设A是不可约矩阵，可知(I+A)n-1>0.

设B=(I+A)n-1A,则B>0,有

B=An+an-1An-1+…+a1A

其中ai>0(i=1,2,…,n-1),所以对任意的i,j∈[n]，有

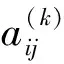
下面引入不可约矩阵的Frobenius定理.

定理2 (Frobenius定理)设A是n阶不可约非负矩阵，则

(1)谱半径ρ(A)>0是A的特征值；

(2) ρ(A)有一个正特征向量x>0;

(3) ρ(A)的代数重数等于1，即ρ(A)是A的单特征值.

因此，不可约非负n阶矩阵总有正特征值ρ(A)(是极大模特征值)，它是特征方程的单根.

证明 这里只对(2)与(3)进行证明.

(2)设A≥0,由引理1可知，谱半径ρ(A)是A的特征值.并且存在非负向量x≥0,x≠0使得Ax=ρ(A)x.

另外，由引理2可知，[1+ρ(A)]n-1x=(I+A)n-1x>0,从而x>0.

(3)如果ρ(A)是A的重特征值，则1+ρ(A)=ρ(I+A)是I+A的重特征值，于是也就有[ρ(I+A)]n-1=ρ[(I+A)n-1]是(I+A)n-1的重特征值，这与(I+A)n-1>0相矛盾.

注 可以证明Frobenius定理有以下推论.

推论3 设不可约矩阵A=An×n≥0,λ1=ρ(A).若A有k个模等于ρ(A)的不同特征值：

{λ1,λ2,…,λk},λ1=ρ(A)

则这些数恰为方程xk=[ρ(A)]k的k个根，并且它们都是A的单特征根.

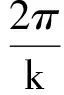
[1] 许以超.线性代数与矩阵论[M].2版.北京：高等教育出版社，2008.

[2] 王永茂.矩阵分析[M].北京：机械工业出版社，2005.

[3] 曾祥金，张亮.矩阵分析简明教程[M].北京：科学出版社，2010.

[责任编辑 马云彤]

Research on the Irreducible Non-negative Matrix

WANG Xin-qi

(Editorial Department of Journal, Xi’an University, Xi’an 710065, China)

This paper introduces the concept of non-negative matrix and irreducible non-negative matrices, discuss the structure of irreducible non-negative matrices, and obtained some useful results, these results are not available in the general matrix.

positive matrix; non-negative matrix; irreducible non-negative matrix

1008-5564(2016)06-0004-03

2016-06-30

国家自然科学基金项目(11371290)

王新奇(1963—)，男，河南洛阳人，西安文理学院学报编辑部主编、副教授、副编审，硕士，主要从事数值代数研究.

O151.21

A