孙冬梅，黄东卫

(天津工业大学 理学院，天津 300387)



一类捕食与被捕食模型的动力学稳定性分析

孙冬梅，黄东卫

(天津工业大学 理学院，天津 300387)

针对一种被捕食者与两种捕食者的密度之间相互关系,建立了描述者间动力学演化行为的数学模型,利用Routh-Hurwitz判别法，分析了模型中各种群演化过程性态的稳定性. 并选取模型中被捕食者密度的增长率为关键参数，得到了该动力系统发生Hopf分岔的条件,对系统进行数值模拟，计算出其Lyapunov指数谱，以及发生Hopf分岔时的参数阈值, 结果表明被捕食者密度参数对系统性态变化起到了关键的控制作用，有助于认识此类系统产生分岔及混沌现象的演化机理.

动力学模型；Routh-Hurwitz判别法；Hopf分岔；Lyapunov指数谱

环境问题是近些年来很重要的问题，影响人类以及生物种群的存在和发展人与生物种群之间的关系问题也是被广泛关注的，所以为了人与自然和谐相处，研究种群成为许多学者感兴趣的课题之一[1].迄今为止，许多科学家做了大量调查并发表了许多论文[2-4].捕食食饵模型是很重要的模型之一，捕食模型主要对生态系统中的捕食者与食饵的关系进行了分析研究，保持各生物种群的稳定，以免使得物种被灭绝，从而使得生态系统达到持久稳定状态，保持生物种群的多样性.所以，研究食饵捕食者之间的相互作用关系具有很重要的意义[5-6].

1 多种群捕食与被捕食模型建立

通过相关的文献资料[7-10]，分析多种群捕食者与被捕食者的生态动力学模型，根据各种群的食物链的反馈机制(如图1所示)捕食者——两种被捕食者，被捕食者被两种捕食者捕食，存在外物补充，两种捕食者存在种内竞争和种间竞争，并且靠捕食被捕食者繁殖.建立反应各生态要素的多参数模型,选取主要影响参数作为控制变量，对捕食者与被捕食者之间的机理进行分析和讨论.

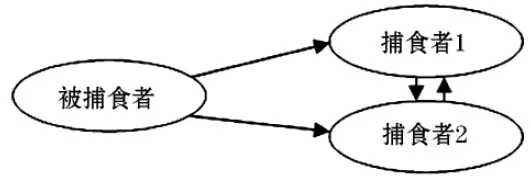
图1 营养关系图

根据捕食者与被捕食者之间的关系形成一个简单生态系统，通过利用多种群生态学原理[11]，建立捕食者与两种被捕食者的动力学模型的表达式为

其中:xi=xi(t),x1表示被捕食者随时间变化的密度，x2,x3分别表示两种捕食者随时间变化的密度；a10为被捕食者內禀增长率，a20和a30分别为两种捕食者內禀增长率；b1和b2共同决定被捕食者密度增长的半饱和参数；a12、a13分别为被两种捕食者捕食的相对减少比例；a21、a31分别为两种捕食者捕食后的转换的增长比例；c1、c2分别为两种捕食者种内竞争减少的比例，d1、d2分别为两种捕食者相互竞争减少的比例.

2 分析系统模型的运动稳定性

根据方程的一些基本特征,考虑食物链模型中各元素的物理意义以及在实际情况中的相互作用和影响.考虑Lyapunov运动稳定性的判定条件及其相关稳定理论去判断上述方程的稳定性.

先求方程的平衡点，令上述方程组的左端为零，即

解上述方程组得平衡点Q(x1*,x2*,x3*).通过坐标平移，可令

则方程可化为

则可得式(1)的Jacobi矩阵K为

对于平衡态Q1(x1,0,0)，此时仅有被捕食者存在，此时可得Jacobi矩阵为

对于平衡态Q1(x1,x2,0)，这时只存在被捕食者和其中一种捕食者，此时的Jacobi矩阵为

此时如果运用特征值判断系统稳定性，由于不确定量太多，不容易进行判断，所以直接运用Routh-Hurwitz判别法去判定系统的稳定性.由Routh-Hurwitz判别法可得三阶方程稳定的条件为:若已知系统特征方程为a3l3+a2l2+a1l+a0=0，则当所有系数均为正数时系统稳定，且要求

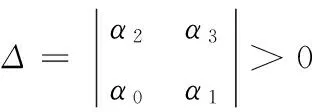
对于平衡态Q1(x1,x2,0)可求得此时系统的特征方程式为

λ3+α2λ2+α1λ1+α0=0

其中:

根据Routh-Hurwitz判别法可知，不等式条件(R)成立时，系统将在平衡态点Q2(x1,x2,0)稳定.

随着参数取值的变化，平衡态Q2(x1,x2,0)出现跨临界分叉和超临界分岔现象.

3 数值模拟

对于平衡态Q3(x1,x2,x3)，此时被捕食者和两种捕食者都存在，此时Jacobi矩阵和特征方程太过繁琐，将采取将参数赋值的方法进行分析说明，这里我们将a10作为控制变量对方程平衡态的稳定性进行研究，取参数a20=0.013 25，a30=0.018，a21=0.4，a12=0.5，a31=0.3，a13=0.4，b1=2，b2=3，c1=0.08，c2=0.02，d1=0.02，d2=0.01.此时各变量的初始值如下：

x(0)=0.8 ，y(0)=0.3，z(0)=0.2；

将各参数代入系统方程，并进行数值模拟，可以发现：当a10在0.01～0.264 6之间变化时，系统的相图将由极限环逐步变化为点之后再呈现极限环状态，此时主要出现两种形态.当在0.264 7～0.264 8之间取值时系统开始出现不稳定状态，此时为系统的分界点.当a10取值大于0.264 8时，系统将呈现发散状态，此时将不存在混沌吸引子，需要人为控制或改变其他控制变量，从而使系统再次达到平衡状态[13].下面主要就三种情况进行详细分析.

以a10为控制变量计算系统的Lyapunov指数(如图2)，由图2可以看出系统的最大Lyapunov指数随着a10的改变而改变，所以，系统的稳定性也

随着a10的改变而改变；当a10<0.28时，系统的最大Lyapunov指数小于零，所以此时系统是稳定的；当a10≥0.28时，系统的最大Lyapunov指数大于零，此时系统处于不稳定状态，系统的Lyapunov指数大幅度增加，系统出现不稳定状态.

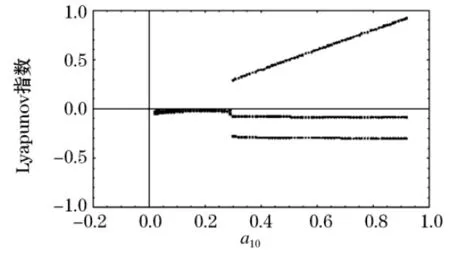
图2 系统关于a10变化时的Lyapunov指数图

当a10=0.22时，通过数值模拟可得系统的相图和各因素的时间历程图见图3.

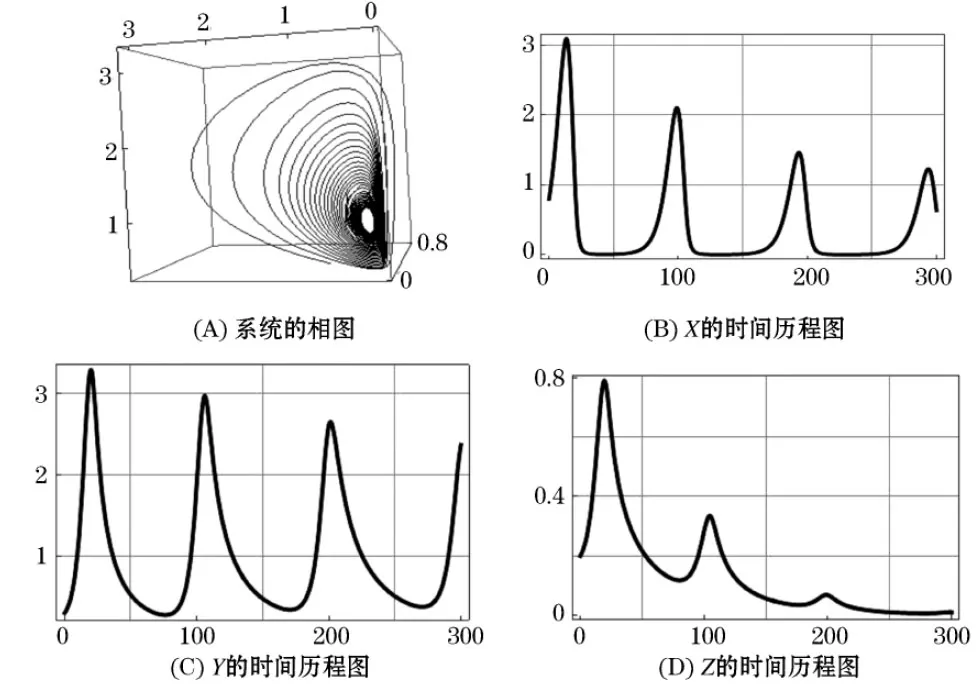
图3 a10=0.22时系统的相图及时间历程图

图3中(A)为系统的相图，(B)为X的时间历程图，(C)为Y的时间历程图，(D)为Z的时间历程图；通过数值模拟结果，主要表明随着时间的发展被捕食者与两种捕食者随时间发生周期性变化，由图像可以看出，此时一种捕食者竞争不过另一种捕食者而灭绝，而没有灭绝的捕食者与被捕食者呈现周期增长，随时间增长系统会达一种平衡状态，呈现出极限环.此时系统是相对稳定的.

当a10=0.145 1时，通过数值模拟得到系统的相图和各因素的时间历程图见图4.

同样由模拟结果可以表明:其中一种捕食者竞争不过另一种捕食者而灭绝，但随着时间的变化，另一种捕食者与被捕食者最后达到了一种稳定的状态，种群的数量变化波动很小，这种状态是相比较稳定的一种状态，此时如果改变其他参数也可以使得灭绝的捕食者被灭绝的时间延长甚至使得三种群的数量最后也都达到一种稳定状态.

图4 a10=0.145 1时系统的相图及时间历程图

当a10>0.264 7时，此时得到的结果没有意义，系统不再出现极限环或平衡态，此时可以改变其他参变量进行人为干预，也可达到一种平衡态，且在较长时间内各物种的变化有一定波动，不会出现灭绝.不妨取a10=0.27，重新定义参数：a21=0.5，a31=0.575，c1=0.0182，a10=0.27，a20=0.02.其余参数不变.通过数值模拟得到系统重新定义参数之前的相图和各因素的时间历程图分别如图5.

图5 a10=0.27时系统的相图及时间历程图

通过图5可以看到，系统是不稳定的，此时被捕食者的在初始时刻的种群密度较小，两种捕食者的种群密度也极不稳定，但一定时间后，被捕食者的种群密度剧增，其中一种捕食者灭绝，另一种捕食者剧增，这种情况极其不稳定，所以此时需要进行人为干预才可以使得系统重新达到一种理想的稳定状态.

通过人为干预重新改变参数后可得到如下的相图和各因素的时间历程图，见图6.

图6 a10=0.27时系统的相图及时间历程图

通过图6可以看出，参变量发生变化后，此时系统重新达到了一种平衡态，在较长时间内，被捕食者和捕食者均波动生长，被捕食者种群密度的增大或减小，直接影响两种捕食者种群密度的增大或减小，各物种不会出现剧增或灭绝状态，这种情况是相对稳定的.

从上面的分析中可以看出，系统的稳定性随a10的不断变化而变化.当a10<0.264 7时，系统是相对稳定的；当a10>0.264 7时，系统是不稳定的，此时要达到稳定状态则需要人为干预，从而使系统再次达到一种平衡态.所以，控制被捕食者的种群密度是维持物种种群平衡的重要因素.因此我们可以得到预防和控制某物种爆发或急剧减少的一种方法:及时检测被捕食者的种群密度，当被捕食者的增长率超过0.27之后，应该及时采取人为干预，改变其他因素，从而改变其他参变量，使得各物种重新处于稳定状态.

4 结 语

本文利用现代动力学理论和系统运动稳定性理论对一类捕食者与被捕食者模型的稳定性作了深入的分析和讨论.结果表明，对于此类多种群的生态动力学系统，当参数变化达到某些阈值时，系统会发生Hopf分岔现象.其他很多文章也对生态系统做了一些分析[14-16]，结合本文可得出系统对应的各种稳定状态是有条件的，参数和实际发生条件是比较一致的.研究结果有助于更好的理解各种捕食者与被捕食者种群动力学行为以及建立更有效的捕食与被捕食模型，具有一定的借鉴意义.但本文也有一些不足，缺乏一定的精确的数据来源.现实中在研究种群竞争时，可以在准确数据来源的基础上更加深入的研究，通过数学的方法使得种群维持在一种稳定状态，并及时给出理论上的分析与建议供相关机构参考.

[1] CUI J, SUN Y. Permanence of predator-prey system with infinite delay [J]. Electronic Journal of Differential Equations I, 2004(81): 1-12.

[2] 黄运金, 张朝阳. 无穷时滞Lotka-Volterra竞争系统的持久性[J]. 福建农林大学学报:自然科学版, 2010, 39(2): 222-224．

[3] 陈兰荪. 数学生态学模型与研究方法[M]. 北京: 科学出版社, 1988. 129-132．

[4] 陈兰荪, 陈 健.非线性生物动力系统[M]. 北京: 科学出版社, 1993.165-170.

[5] 王洪礼, 冯剑丰, 沈 菲, 等. 赤潮藻类非线性动力学模型的分岔及稳定性研究[J]. 应用数学和力学, 2005, 26(6): 671-676.

[6] 马知恩. 种群生态学的数学建模与研究[M]. 合肥: 安徽教育出版社, 1996. 16-159.

[7] 岳宗敏, 胡志兴. 一类具功能反应的食饵-捕食两种群模型的极限环的唯一性[J]. 生物数学学报, 2005, 20(2): 169-172.

[8] YANG W, LI X, BAI Z. Permanence of periodic Holling type-IV predator-prey system with stage structure for prey[J]. Mathematical and Computer Modelling, 2008, 48: 677-684.

[9] LU C, DING X, LIU M. The numerical simulation of periodic solutions for a predator-prey system[J]. Computers and Math with Applications, 2010, 59: 868-879.

[10] YAN X P, ZHANG C C. Hopf bifurcation in a delayed Lokta-Volterra predator-prey system[J]. Nonlinear Analysis Real World Applications, 2008, 9(1): 114-127.

[11] LV J, WANG K. Asymptotic properties of a stochastic predator-prey system with Holiing II functional response[J]. Commun Nonlinear SciNumer Somulat, 2011, 16: 4037-4048.

[12] WANG L L, LI W T. Periodic solutions and permanence for a delayed nonauton-omous ratio-dependent predator-prey model with Holling type functional response[J]. Comput Appl Math, 2004, 162: 341-357.

[13] FENG W. Dynamics in 3-species predator-prey models with time delays[J]. Discrete and Continuous Dynamical Systems, 2007, supplement: 364-372.

[14] TOAHA S, HASSAN M A. Stability analysis of predator-prey population model with time delay and constant rate of harvesting[J]. Journal of Mathematics, 2008, 40: 37-48.

[15] GE Z H, HE Y N. Diffusion effect and stability analysis of a predator-prey system described by a delayed reaction-diffusion equations [J]. J Math Anal Appl, 2008, 339: 1432-1450.

[16] CUI R H, SHI J P, WU B Y. StrogAllee effect in a diffusive predator-prey system with a protection zone[J]. J Diff Equns, 2014, 256: 108-129.

Stability analysis of dynamical model of two predators and one prey

SUN Dong-mei, HUANG Dong-wei

(School of Science, Tianjin Polytechnic University, Tianjin 300387, China)

In this paper, the interrelation between the density of two predators and one prey was investigated, and a mathematical model was established to describe dynamical behaviors between the three. The stability state of system was analyzed and judged by Routh-Hurwitz criterion. And chose the increase rate of the density of prey growth as the key parameter, could get the conditions for Hopf bifurcation occurrence in the system. And calculated the Lyapunov exponent spectrum, and presented simulation results of the system, and obtained the threshold parameter of Hopf bifurcation occurrence. The results showed that the density of prey played a vital role in the change of system state，which would be helpful to understand and identify the evolutionary mechanism of bifurcation and chaos phenomena of the system.

dynamical model; Routh-Hurwitz criterion; Hopf bifurcation; Lyapunov exponent spectrum

2016-05-25.

国家自然科学基金项目(11501410).

孙冬梅(1991-)，女，硕士，研究方向：非线性动力系统理论及应用.

黄东卫(1966-)，男，博士，教授，硕士生导师，研究方向：非线性动力系统理论及应用.

O175

A

1672-0946(2016)06-0697-06