江俊勤，沈华嘉

（广东第二师范学院 物理系，广东 广州 510303）

有限深多势阱中电子能态的数值研究

江俊勤，沈华嘉

（广东第二师范学院 物理系，广东 广州 510303）

研究处于N个有限深对称势阱中的电子态.从薛定谔方程出发，在N=1、2、3和4的情况下，用Mathematica数值求解由标准条件决定的线性方程组，精确计算出电子的能级和波函数.直观地展示电子能级分裂成能带的机理.

数值分析；有限深多势阱；定态薛定谔方程；能级和波函数；能带

计算一维有限深势阱中电子的能级和波函数，是量子力学教学中一个重要的问题.这个问题的经典解法是：先分区间求出薛定谔方程的解析解，然后利用波函数的标准条件确定电子的能级和波函数.经典解法的优点是物理概念清晰、计算过程简明易懂.然而，即使在单势阱的情况下，决定能级个数和大小的是颇为复杂的超越方程，所以教科书［1-3］最后只能定性地讨论能级的取值范围.要得到足够精度的能级并确定具体的波函数，需要进一步利用电子计算机进行有效的数值计算.对于N个势阱情况，更需要一种有效的数值计算方法.

在保留经典解法优点的前提下，本文发展了一种基于通用软件 Mathematica的有效计算电子能态的数值方法.在N=1、2、3和4的情况下进行具体的计算，并研究能级结构随N变化的规律.

1 电子能级的计算

1.1 单势阱

考虑单个电子被如图1所示的势阱束缚着（电子能量E＜U0，U0＞0）：左右两边的势垒为无限宽但有限高，高度为U0，即势能函数可写为

现有资料多数把坐标原点建在势阱底部中间，并分奇宇称和偶宇称两种情形进行计算［1-3］.笔者认为：既然问题的解答最终需要通过计算机软件做数值计算，就不必事先由人工区分奇偶宇称了，波函数是否奇偶宇称还是用数值计算的结果来说明吧.研究表明，取如图1所示的坐标系更为方便（对于多个势阱情况更有优势）.

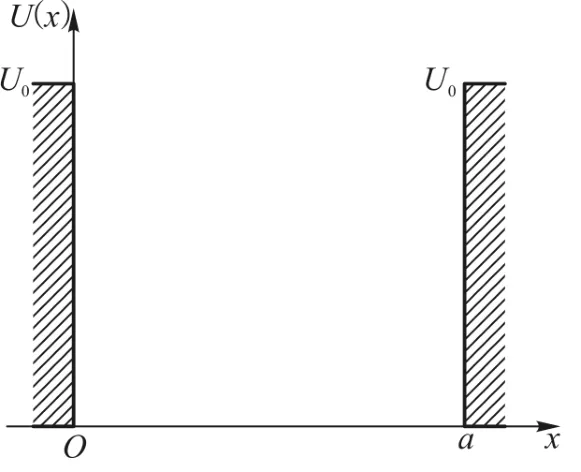
图1 单势阱示意图

势阱的定态薛定谔方程只需分3个区间求解：

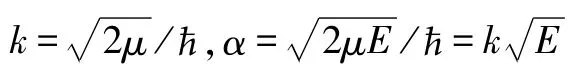
当0＜x＜a时，令（μ为电子质量，ħ为约化普朗克常量），则定态薛定谔方程可化为

上式的通解为

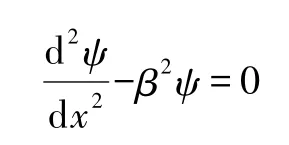
上式满足ψ（±∞）为有限值要求的解为

根据波函数（及其一阶导数）的连续性要求，在x=0处，要求ψ（0-）=ψ（0+）和ψ′（0-）=ψ′（0+），即

这就是取如图1所示坐标系的好处之一，x=0处的边界条件可以提前单独处理，这样，当 0＜x＜a时波函数可写成

在x=a处，要求 ψ（a-）=ψ（a+）且 ψ′（a-）= ψ′（a+），即

图2 单个势阱中f（E）的曲线图

图3 双势阱示意图

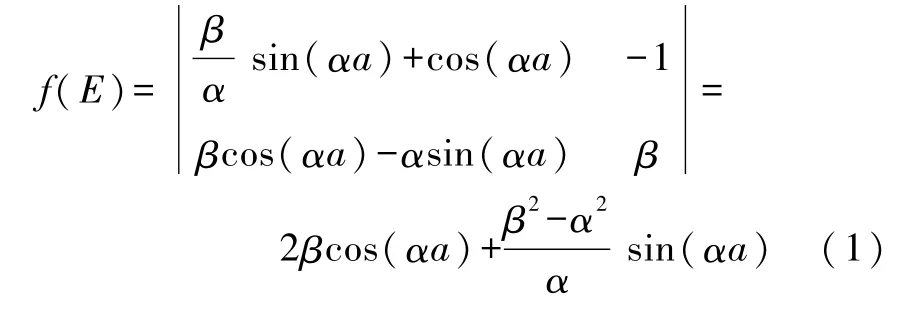
f（E）=0的全部实数根就是所求的本征能量（体系的能级）.然而，想求出足够精度的本征能量，必须进行有效的数值计算，借助 Mathematica的找根命令 FindRoot（用牛顿法）可完美解决，为此可先用命令 Plot画出 f（E）的曲线图，确定各个区间内的初值（包括个数，避免遗漏）.若取a=10 Å和U0=5 eV，则 f（E）的曲线如图 2所示，共有4个能级，它们的大概值分别是 0.3、1.2、2.3和4.1，以此为初值，容易求得高精度的能级（单位为eV，下同；默认精度为16位有效数字，取6位已足够精确），分别为：0.271 803、1.077 39、2.379 20和4.059 33.

1.2 双势阱

以势阱左下角为原点的另一个优势是便于推广到双势阱的情况.设单个电子被如图3所示的双势阱束缚着（电子能量 E＜U0）.3个阱壁（势垒）的高度都为U0，左右两边的阱壁无限宽，中间势垒的宽度为w=a2-a1.定态薛定谔要分5个区间求解.根据单个势阱的求解经验，容易求得满足 ψ（±∞）为有限值的波函数：

各未知系数和能量由 x=0、a1、a2、a3处定态波函数（及其导数）的连续性确定.

先由x=0处连续性要求得A1=βA／α和A2=A，再由 x=a1、a2、a33处连续的要求，得

式（3）是6元齐次线性方程组，有非零解（有非平庸解）的充要条件是系数行列式为零，约去公因子exp（-βa3），得到确定能量本征值的条件：

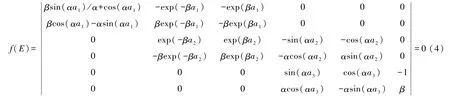
行列式f（E）的计算对于Mathematica来说是很容易的，直接输入即可.与单势阱的处理方法一样，先画曲线图确定能级个数及大概位置（初值），再找根命令FindRoot求出高精度能级.

本文的计算方法适合于任意势阱（不限于对称势阱）.先考虑非对称双势阱，取 a1=10 Å、a2=12 Å、a3=27 Å（两势阱的宽度分别为10 Å和15 Å、中间势垒宽度是2 Å）以及U0=5 eV，则f（E）的曲线如图4所示，能级共有10个，它们的大概值分别为0.13、0.27、0.51、1.1、1.3、2.1、2.5、3.2、4.1和4.6，以此为初值，容易求得高精度的能级，分别为：0.133 609、0.271 090、0.533 465、1.067 72、1.202 45、2.091 01、2.393 94、3.246 42、4.073 09和4.615 08.

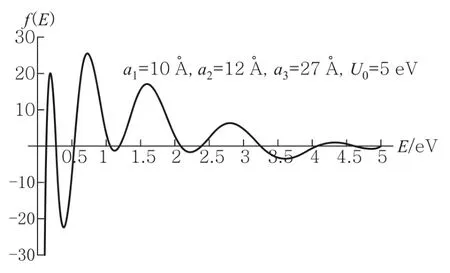
图4 双个势阱中f（E）的曲线图

我们更感兴趣的是对称多势阱，取a1=10 Å、a2=15 Å、a3=25 Å和 U0=5 eV，即两个势阱的宽度都是10 Å，而中间势垒宽度是5 Å，则能级一共有8个，分别为：0.271 504、0.272 100、1.075 65、1.079 13、2.371 58、2.386 91、4.025 56和4.099 41.

这8个能级有两两成对的趋势.增大中间势垒的宽度，这种趋势更加明显，若取 a1=10 Å、a2= 30 Å、a3=40 Å和 U0=5 eV，则 8个能级分别为：0.271 803、0.271 803、1.077 39、1.077 39、2.379 20、2.379 20、4.059 31和4.059 35.

可见，当中间势垒的宽度（即两个势阱的距离）增大为w=a2-a1=20 Å（为势阱宽度的两倍）时，双势阱的能级与两个独立单势阱的情况几乎完全一样，只有最高的能级有很微小的差别.

相反，若减少中间势垒的宽度（即缩小势阱的距离），则能级分裂增大，当取 a1=10 Å、a2=12 Å、a3=22 Å（即w=2 Å）和 U0=5 eV时，能级分别为：0.262 728、0.279 664、1.039 20、1.112 31、2.290 04、2.473 76、3.928 55和4.280 98.

1.3 多势阱

单势阱和双势阱的计算方法不难推广到多势阱的情况.每增多一个势阱，定态薛定谔的求解区间增加两个：波函数增加两段、确定能级的齐次线性方程组增加4个未知量.

对于3势阱，波函数分为7段：

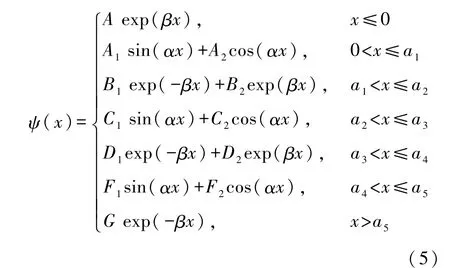
由x=0、a1、a2、a3、a4、a5处定态波函数（及其导数）的连续性可确定各未知系数和能量：

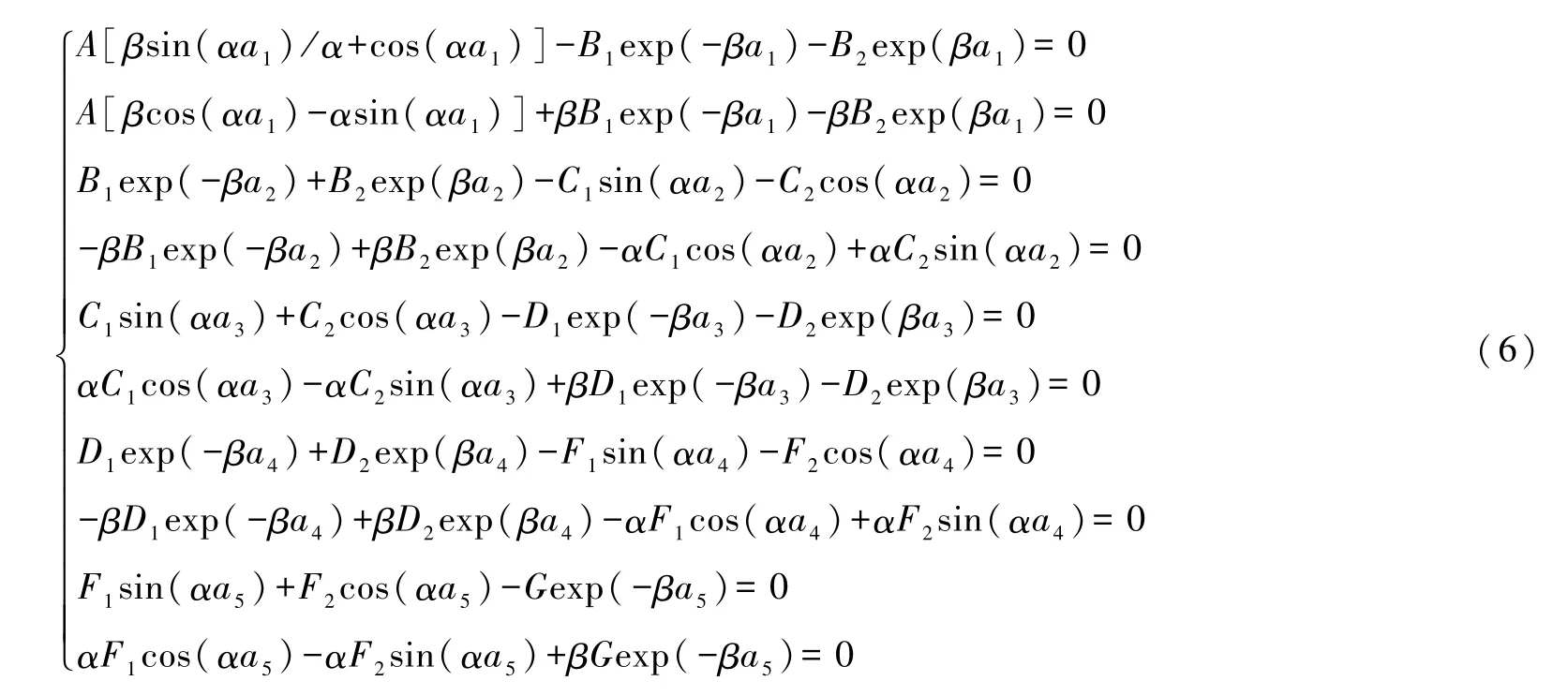
式（6）是十元齐次线性方程组，其系数行列式（10阶）f（E）等于零是确定能量本征值的条件，处理方法与求解双势阱的情况完全一样.取a1=10 Å、a2=15 Å、a3=25 Å、a4=30 Å、a5=40 Å（即每个势阱的宽度都是 10 Å，而中间势垒宽度都是 5 Å）和U0=5 eV，容易求得所有能级（共 12个），分别为：0.271 38、0.271 802、0.272 223、1.074 93、1.077 39、1.079 85、2.368 46、2.37 9 19、2.390 13、4.012 23、4.061 24和4.117 22.它们每3个成1组.

对于四势阱，波函数分为9段，确定能级和波函数系数的是14元齐次线性方程组，由14阶系数行列式f（E）等于零（有非零解的条件）可求得所有能级.仍然取每个势阱的宽度都是10 Å、中间势垒宽度都是 5 Å （即 a1=10 Å、a2=15 Å、a3=25 Å、a4=30 Å、a5=40 Å、a6=45 Å、a7=55 Å）和 U0= 5 eV，则共有 16个能级，分别为：0.271 319、0.271 617、0.271 986、0.272 284、1.074 57、1.076 31、1.078 46、1.080 21、2.366 92、2.374 47、2.383 95、2.391 73、4.005 74、4.039 42、4.085 07和 4.126 19.它们每4个成1组.

为了便于比较，现将1个至4个对称势阱的能级绘制在一幅图上，如图5所示，由于势阱之间距离比较近（5 Å），N个完全一样的势阱组合在一起时，电子的波函数发生了重叠（特别是高能级的电子态），电子感受到了各个势阱的影响，原来的每一个能级分裂成N个相近的新能级，N越大能级间隙越小，形成了能带.

2 本征波函数的计算

图5 1至4个对称势阱中电子的能级图

以3势阱（N=3）为例.把能级 E、电子质量μ、电量e、约化普朗克常量ħ和U0值代入式（6），就可以确定各个系数与A之间的关系（A由归一化条件给出）.事实上，第一和第二两个系数已经提前确定A1=βA／α和A2=A；由式（6）的前两个方程可以唯一确定B1和B2，由第三和第四个方程唯一确定C1和C2，由第五和第六个方程唯一确定D1和 D2，由第七和第八个方程唯一确定F1和F2，最后由式（6）的第九个（或者第十个）方程唯一确定G；把各个系数代入式（5）就可以计算波函数并绘图，当然所有的计算全部交给Mathematica去完成.限于篇幅，本文只给出前3个和第12个（即最后一个）波函数，分别如图6-图9所示.

图6 对称三势阱中电子基态的波函数

图7 对称三势阱中电子第一激发态的波函数

图9 对称三势阱中电子最高激发态的波函数

波函数是以势阱中心轴（x=20 Å）为对称轴的奇偶函数，这是数值计算的自然结果，无需在计算前先分类.随着能级的变化，奇偶性轮流出现，基态为偶函数，能量最高的态为奇函数.

3 结论与讨论

本文研究处于N个有限深对称势阱中的电子态，保留了经典解法的优点，从薛定谔方程出发，发展了一种基于通用软件 Mathematica的数值方法---通过数值求解由标准条件决定的线性方程组，计算出电子的能级和波函数.并在N=1、2、3和4的情况下进行具体的计算，结果表明：本方法不但物理概念清晰、过程简明易懂，而且计算精度高、速度快，方便于任意多势阱的计算（不限于对称势阱）.同时，本文结果能直观地展示电子能级分裂成能带的机理，这对于能带结构的教学也是有意义的.

关于有限深对称势阱中的电子能级问题，也可以使用其他算法，例如：节点法、近似的初值计算法［4］，但这些方法过于“专门”，脱离了传统教科书的经典解法，不太适合在教学中使用.

［1］ 曾谨言.量子力学教程［M］.北京：科学出版社，2003：34-36.

［2］ 朱栋培.量子力学基础［M］.安徽：中国科学技术大学出版社，2012：41-46.

［3］ 苏汝铿.量子力学［M］.上海：复旦大学出版社，1997：37-40.

［4］ 董建.Mathematica与大学物理计算［M］.2版.清华大学出版社，2013：309-318.

Numerical study of electronic states in finite multiple potential wells

JIANG Jun-qin，SHEN Hua-jia
（Department of Physics，Guangdong University of Education，Guangzhou，Guangdong 510303，China）

The electronic states in the symmetric N-potential wells are studied.Based on the Schrödinger equation，the linear equations determined by the standard conditions in the case of N=1，2，3 and 4 are solved，the energy level and wave function are accurately calculated by using Mathematica.The mechanism of the energy level splitting into energy band is exhibited.

numerical analysis；finite multiple potential wells；Schrödinger equation；energy level and wave function；energy bands

O 413.1

A

1000-0712（2016）11-0013-05

2015-11-23；

2016-03-01

广东省高等学校物理专业综合改革试点项目资助

江俊勤（1962-），男，广东揭阳人，广东第二师范学院物理系教授，主要从事量子力学教学和格点规范场论的研究工作.