潘 理,郑 红,刘显明,杨 勃

(1.湖南理工学院信息与通信工程学院,湖南岳阳 414006;2.华东理工大学信息科学与工程学院,上海 200237;3.江西省电力公司信息通信分公司,江西南昌 330077)



基于Petri网局部性的极大冲突集枚举算法

潘 理1,郑 红2,刘显明3,杨 勃1

(1.湖南理工学院信息与通信工程学院,湖南岳阳 414006;2.华东理工大学信息科学与工程学院,上海 200237;3.江西省电力公司信息通信分公司,江西南昌 330077)

冲突是Petri网研究的重要主题.目前Petri网冲突研究主要集中于冲突建模和冲突消解策略,而对冲突问题本身的计算复杂性却很少关注.提出Petri网的冲突集问题,并证明冲突集问题是NP(Non-deterministic Polynomial)完全的.提出极大冲突集动态枚举算法,该算法基于当前标识的所有极大冲突集,利用Petri网实施局部性,仅计算下一标识中受局部性影响的极大冲突集,从而避免重新枚举所有极大冲突集.该算法时间复杂度为O(m2n),m是当前标识的极大冲突集数目,n是变迁数.最后证明自由选择网、非对称选择网的极大冲突集枚举算法复杂度可降至O(n2).极大冲突集枚举算法研究将为Petri网冲突问题的算法求解提供理论参考.

Petri网;冲突集问题;NP(Non-deterministic Polynomial)完全性;极大冲突集枚举算法

电子学报URL:http://www.ejournal.org.cn DOI:10.3969/j.issn.0372-2112.2016.08.013

1 引言

冲突是Petri网理论的重要概念.冲突的本质是资源竞争[1].当多个冲突变迁竞争有限资源,若其中一个获得资源,其它与之冲突的变迁就会丧失使能.若变迁集合中的任意两个变迁都是冲突的,称这个集合为冲突集.现有Petri网冲突研究主要集中于冲突处理策略和冲突问题建模.经典Petri网采用不确定选择策略处理变迁冲突[2];优先级Petri网通过设置优先级来解决冲突[3];时间Petri网则利用时间竞争来处理变迁之间的冲突[4];谓词/变迁网通过谓词来控制冲突变迁的实施[5];随机Petri网则引入某种实施概率分布来处理变迁间的冲突[6,7].在建模方面,近期Zeng等利用Petri网方法探讨应急响应过程中资源冲突侦测和消解[8];Tian等利用时间Petri网的时间约束特性处理实时系统的冲突问题[9];Popescu等利用Petri网方法解决面向服务制造系统调度过程中的资源冲突[10].

上述研究注重冲突问题建模及冲突消解策略,而对冲突问题本身的计算复杂性却很少关注.现实系统中的冲突情况往往非常复杂,枚举系统的极大冲突集,对于全面了解系统冲突、寻求冲突消解方案是非常重要的.因此,对冲突集问题复杂度进行界定,并提出基于Petri网特征的枚举算法,将为Petri网冲突问题的计算求解提供一种探索途径.目前已有大量文献研究Petri网的死锁问题、活性问题、可达性问题、合法实施序列问题、合成问题、步问题等,得出了一系列有价值的计算复杂性结论[11-16].但这些结论并没涉及冲突集问题.本文尝试以冲突集问题为研究对象,通过从已知NP完全问题归约到冲突集问题,证明冲突集问题的NP完全性;然后利用Petri网实施的局部性特征,提出动态枚举算法,降低极大冲突集枚举的计算成本,为冲突集问题的复杂性研究提供有益参考.

2 冲突集问题

2.1 基本定义

用N表示自然数集{0,1,2,…},用Z+表示正整数集.

定义1[1]一个Petri网是一个四元组Σ=(P,T,F,M0),其中:

(1)P是库所集;(2)T是变迁集,且P∩T=∅;(3)F⊆(P×T)∪(T×P)是流关系;(4)M0:P→N是初始标识.

标识M可表示为一个|P|元向量,第i个元素表示库所pi中的令牌数.流关系F可表示为特征函数的形式,即F:(P×T)∪(T×P)→{0,1}.用·p={t|(t,p)∈F}和p·={t|(p,t)∈F}表示库所p的输入变迁集和输出变迁集;类似的,用·t和t·表示变迁t的输入库所集和输出库所集.

定义2[1]一个变迁t∈T在标识M是使能的,当且仅当∀p∈P,F(p,t)≤M(p).用En(M)表示标识M下所有使能变迁的集合.

定义3[1]如果tf在标识M是使能的,那么tf可以实施并产生一个新的后继标识M′,且∀p∈P,M′(p)=M(p)-F(p,tf)+F(tf,p).

定义4[1]给定t1,t2∈En(M),若∀p∈P,使F(p,t1)+F(p,t2)>M(p),则称变迁t1和t2在标识M是(有效)冲突的,用t1Mt2表示.

定义5 给定一个变迁集U⊆T,如果∀t1,t2∈U,有t1Mt2,则U是标识M的一个冲突集.若不存在其它冲突集U′,使U⊂U′,则称U是M的极大冲突集.用MCS(M)表示在标识M下的所有极大冲突集的集合.

2.2 冲突集问题

定义6[17]复杂类P表示用确定型图灵机在多项式时间内可解决的判定问题集,NP表示用非确定型图灵机在多项式时间内可解决的判定问题集.

定义7[17]若判定问题A属于NP,且所有其它NP问题都能多项式时间多一归约到A,则称A是NP完全的.

引理1[17]对于判定问题A,若存在NP完全问题B,使B多项式时间多一归约到A,则A是NP困难的.若A是NP困难的且A∈NP,则A是NP完全的.

定义8 (冲突集问题,CS)给定Petri网Σ=(P,T,F,M0),标识M∈RS(M0)和正整数k≤|T|,问在标识M是否包含变迁数至少为k的冲突集?

接下来,通过从已知NP完全问题(团问题)归约到冲突集问题,来证明冲突集问题的NP完全性.

设G=(V,E)是简单无向图,这里V是顶点集,E是边集.给定一个顶点子集A⊆V,用G(A)表示由A诱导的子图.

定义9[18]给定图G=(V,E),如果∀u,w∈V,有(u,w)∈E,则称G是完全的.若G(Q)是完全图,则称Q是G的一个团.

定义10[18](团问题,CLIQUE)给定简单无向图G=(V,E)和正整数k≤|V|,问G是否包含基数至少为k的团?

引理2[18]团问题是NP完全的.

定理1 冲突集问题是NP完全的.

证明 (1)首先证明冲突集问题是NP困难的.

考虑从团问题多项式时间多一归约到冲突集问题.设简单无向图G=(V,E)和正整数s是团问题的一个实例,要构造冲突集问题的一个实例:Petri网Σ、标识M和正整数k,使Σ在标识M有一个大小至少为k的冲突集当且仅当G有一个大小至少为s的团.按照下面的方式进行构造:

(ⅰ)vi∈V当且仅当ti∈T,即Petri网Σ中的每个变迁t1,t2,…,tn对应图G中的每个顶点v1,v2,…,vn.

(ⅱ)(vi,vj)∈E当且仅当pij∈P∧M(pij)=1∧F(pij,ti)=1∧F(pij,tj)=1.换句话说,两顶点vi和vj相邻当且仅当ti与tj共享输入库所pij,库所pij中放置1个令牌,且弧(pij,ti)和(pij,tj)的权值均为1.

(ⅲ)vi是孤立点当且仅当pi∈P∧M(pi)=1∧F(pi,ti)=1.即vi是孤立点当且仅当ti有一个输入库所pi,库所pi中放置1个令牌,且弧(pi,ti)的权值为1.

(ⅳ)k=s.

从上面构造可以看出,Petri网Σ的每个变迁对应图G的每个顶点,且每个变迁在M都使能;两个变迁共享一个库所当且仅当图G中对应的两个顶点是相邻的.如图1(a)所示,图G有4个顶点v1,v2,v3,v4,其中包含一个s=3的团{v1,v2,v3}.通过上述构造得到Petri网Σ和标识M,如图1(b)所示,Σ有4个变迁t1,t2,t3,t4,4个库所p12,p13,p23,p4,每个库所中都有1个令牌,4个变迁均使能.容易看出,Petri网Σ在M包含一个k=3的冲突集{t1,t2,t3}.

现在证明Petri网Σ在标识M有一个大小至少为k的冲突集当且仅当G有一个大小至少为s的团.Q是G的一个团且|Q|≤s,当且仅当∀vi,vj∈Q,(vi,vj)∈E;由上面构造步骤,当且仅当得到对应的变迁集U,|U|=|Q|,U⊆En(M)且∀ti,tj∈U,F(pij,ti)+F(pij,tj)>M(pij);即U在标识M是一个冲突集且|U|≤k.

进一步分析这是一个多项式时间的构造.设|V|=n,则V,E和k的输入长度分别为O(n),O(n2)和O(n),故实例的输入总长度是O(n2).构造步(ⅰ)根据顶点集V确定变迁集T,故|T|=n;构造步(ⅱ)和(ⅲ)根据边集E确定库所集P,故|P|=O(n2);标识M的规模是|P|=O(n2),流关系F的规模是|P‖T|=O(n3).因此整个构造需时间O(n3),即从CLIQUE能多项式时间归约到冲突集问题.由于CLIQUE是NP完全的(引理2),根据引理1,冲突集问题是NP困难的.

(2)证明冲突集问题属于NP.

对于Petri网Σ,对任何标识M∈RS(M0),给出一个验证冲突集问题的非确定型算法(见算法1).

假设|P|=m,|T|=n.则P,T,F,M和k的长度分别是O(m),O(n),O(mn),O(m)和O(n),故输入的总长度是O(mn).U的长度是O(n),验证(ⅰ)需时间O(n),验证(ⅱ)需时间O(mn2),故验证(ⅰ)和(ⅱ)需时间O(mn2).这是一个能在多项式时间内验证冲突集问题的非确定型算法.因此冲突集问题属于NP.

综合(1)和(2)的证明,根据引理1,冲突集问题是NP完全的.证毕.

3 极大冲突集枚举算法

3.1 极大冲突集枚举问题

定义11[17]复杂类FP表示用确定型图灵机在多项式时间可解决的函数问题集.

定义12 (极大冲突集枚举问题)给定Petri网Σ=(P,T,F,M0)和标识M∈RS(M0),求Petri网Σ在标识M的所有极大冲突集.

Petri网的极大冲突集枚举问题,可以使用已有的极大团枚举算法来求解.不幸的是,极大团枚举问题是一个已知的NP困难问题.求解这个问题最有效的算法是由Bron和Kerbosch提出的分支限界算法[19],文献[20]证明这种算法在最坏情况下的时间复杂度为O(nn/3).幸运的是,Petri网的实施具有局部性特征.每一次变迁实施仅仅改变与该变迁相关的前集和后集.因此,每一次变迁实施之后,并不需要重新生成所有的极大冲突集,而只需考虑受实施变迁局部环境影响的那些极大冲突集,这无疑将降低极大冲突集枚举问题的计算复杂度.3.2 极大冲突集枚举算法

接下来讨论极大冲突集枚举问题的算法求解.为了简化算法描述,我们假设Petri网是安全的.用MCS(M,ti)表示在标识M下包含变迁ti的极大冲突集的集合.进一步,用MCS(M,S)表示包含S中所有变迁的极大冲突集的集合,即这些极大冲突集均包含变迁子集S.

Petri网变迁实施可分为两步,第一步根据流关系,从变迁的输入库所中取出相应数量的令牌;第二步根据流关系,将相应数量的令牌放置到变迁的输出库所.第一步可能使某些原来冲突的变迁变为不冲突,第二步可能新增一些冲突关系.下面根据影响冲突关系变化的两个步骤,定义两个相应的基本操作:

(1)操作del(M,t):执行M-F(·,t),删除不再冲突的关系；(2)操作add(M,t):执行M-F(·,t)+F(t,·),添加新的冲突关系.

用Dis(M,t)=En(M)En(M-F(·,t))在标识M实施t后丧失使能的变迁集.操作del(M,t)如算法2所示.对标识M下的每个极大冲突集c,在标识M-F(·,t),若c包含非使能变迁,则删除非使能变迁.再判断c是否包含在其它极大冲突集中,若包含,则说明c不是标识M-F(·,t)的极大冲突集,删除c.

设|T|=n,|MCS(M)|=m.变迁t的实施通常只会影响少量极大冲突集,但最坏情况下,可能涉及绝大多数极大冲突集.因此,求解MCS(M,c)通常需O(n),但最坏情况下需O(mn).若循环m次,则该操作的时间复杂度通常为O(mn),最坏情况下为O(m2n).

用Newly(M,t)=En(M′)En(M-F(·,t))表示在新标识M′=M-F(·,t)+F(t,·)新使能的变迁集合.操作add(M,t)如算法3所示.对每个新使能的变迁ti,若ti不与任何极大冲突集相冲突,则ti独自构成极大冲突集;若ti与某个极大冲突集c的所有变迁冲突,则ti并入c;若ti与极大冲突集c的部分变迁冲突,且这部分变迁不是其它极大冲突集的子集,则ti与部分变迁构成新的极大冲突集.

设|T|=n,|MCS(M)|=m,|Newly(M,t)|=k.外层for循环k次,内层for循环m次,内层循环体通常需O(n);最坏情况下变迁实施影响多数极大冲突集,则需O(mn).故整个算法通常情况需O(kmn),最坏情况下需O(km2n).极大冲突集动态枚举算法enum(M,t)如算法4所示,算法思路如下:若在标识M实施变迁t,首先使用del(M,t)从所有极大冲突集中删除丧失使能的变迁,计算得到标识M-F(·,t)的极大冲突集;然后在标识M-F(·,t)+F(t,·),对所有新增使能变迁,使用add(M,t)添加新的冲突关系,得到新标识下所有极大冲突集.

由于新使能变迁数k通常远小于变迁数n,根据del和add操作的复杂度分析,极大冲突集动态枚举算法的时间复杂度通常情况为O(mn),最坏情况下需O(m2n).下面举例说明极大冲突集动态枚举算法.如图2所示.

在初始标识M0=(1 1 1 0 1 0),En(M0)={t1,t2,t3,t4,t7},使用add(M0,λ)得到MCS(M0)={{t1,t2},{t2,t3},{t4},{t7}},这里λ是空变迁.

4 特殊子问题

下面介绍三种典型的特殊子网:自由选择网、扩展自由选择网和非对称选择网.

定义13[2]给定Petri网Σ=(P,T,F,M0),且所有弧的权值为1.

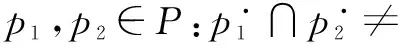
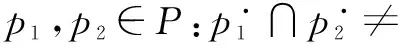
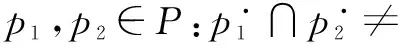
已经证明,这三种子网具有包含关系:FC⊆EFC⊆AC[7].因此,从AC获得的结论,对FC和EFC仍是有效的.定义变迁集T上的结构冲突关系R={(t1,t2)∈T2|·t1∩·t2≠∅}.

定理2 对于非对称选择网,结构冲突关系R是等价关系.

证明 ∀t∈T,有·t∩·t≠∅,即(t,t)∈R,故R是自反的.

∀t1,t2∈T,若(t1,t2)∈R,即·t1∩·t2≠∅,则·t2∩·t1≠∅,即(t2,t1)∈R,故R是对称的.

因此R是等价关系.证毕.

用[t]={t(|t∈T∧(t,t′)∈R}表示t关于R的等价类.

定理3 若t是AC的一个变迁,则∃p∈·t,使p·=[t].

证明 根据AC的定义,∀p′,P∈·t,有p′·⊆p·或p·⊆p′·,故⊆是一个全序关系.由于·t是有限集,故必有最大元,不妨设为p·.又∀ti∈ [t],有·t∩·ti≠∅,不妨设pi∈·t∩·ti,于是t∈p·∩pi·,故pi·⊆p·或p·⊆pi·.由于p·是·t上关于⊆的最大元,即有pi·⊆p·,故得ti∈p·.于是p·⊇ [t].

假设∃ti∈p·但ti[t],则有p∈·t∩·ti,即(t,ti)∈R,于是有ti∈[t],矛盾.因此,p·= [t].证毕.

依据等价关系R,可以将变迁集划分成互不相交的子集,每个子集就是一个等价类.因此,每个变迁仅属于一个等价类.

定理4 若t∈En(M),则(·t)·∩En(M)是极大冲突集.

证明 由定理3可知,(·t)·是t关于R的等价类[t],即等价类中的变迁相互冲突,因此(·t)·∩En(M)是冲突集;又[t]中变迁不属于任何其他等价类,因此(·t)·∩En(M)是极大冲突集.证毕.

定理5 对于非对称选择网,求解极大冲突集枚举问题的时间复杂度为O(n2),这里|T|=n.

证明 非对称选择网的极大冲突集枚举算法如算法5所示.首先算法初始化MCS(M)为空集.然后求出每个变迁的关于有效冲突关系R的等价类,每个等价类即为一个极大冲突集.

先证明算法的正确性.

(ⅰ)由于En(M)是有限集,故for循环的次数是有限的.它根据等价类产生极大冲突集,因此for循环执行完成后,极大冲突集的数目不超过|En(M)|.因此算法一定会终止.

(ⅱ)根据定理4,对任何ti∈En(M),(·ti)·∩En(M)是一个极大冲突集.由定理2和定理3可知,根据冲突关系R,可以将En(M)中所有变迁划分到不同的等价类(极大冲突集),且每个使能变迁对应一个等价类(极大冲突集).在循环过程中,每得到一个等价类,就会从En(M)中删除该等价类中所有变迁,因此,不会出现重复的极大冲突集.因此算法最终返回的MCS(M)一定包含所有极大冲突集.

再分析算法的复杂性.设|T|=n.循环次数不超过n,每次循环需时间O(n),因此整个算法需时间O(n2).证毕.

5 结论

冲突的本质是系统资源的竞争,对冲突问题的研究是Petri网的重要主题之一.本文提出Petri网的冲突集问题,并利用Petri网的实施局部性,提出极大冲突集枚举动态算法.文章的主要结论有:(1)Petri网的冲突集问题是NP完全的;(2)所提极大冲突集枚举算法的时间复杂度为O(m2n),其中m是当前标识的极大冲突集数目,n是变迁数;(3)极大冲突集枚举问题对自由选择网、非对称选择网的复杂度为O(n2).下阶段工作将运用上述研究结论,探索混合语义时间Petri网模型的调度策略[21],处理调度过程中面临的资源冲突问题,并应用于柔性制造系统、工作流系统的调度问题研究.

[1]Girault C,Valk R.Petri Nets for Systems Engineering:A Guide to Modeling,Verification,and Applications[M].Berlin:Springer-Verlag,2013.

[2]Murata T.Petri nets:Properties,Analysis and Applications[J].Proceedings of the IEEE,1989,77(4):541-580.

[3]Yen H C.Priority conflict-free Petri nets[J].Acta informatica,1998,35(8):673-688.

[4]Merlin P M,et al.Recoverability of communication protocols-Implications of a theoretical study[J].IEEE Transactions on Communications,1976,24(9):1036-1043.

[5]Genrich H J.Predicate/Transition Nets[M].Berlin:Springer-Verlag Petri Nets:Central Models and Their Properties,1987.

[6]林闯.随机 Petri 网和系统性能评价[M],北京:清华大学出版社,2009.

[7]Balbo G.Introduction to Stochastic Petri Nets[M].Berlin:Springer-Verlag Lectures on Formal Methods and PerformanceAnalysis,2001.

[8]Zeng Q,Liu C,Duan H.Resource conflict detection and removal strategy for nondeterministic emergency response processes using Petri nets[J].Enterprise Information Systems,2015:1-22.

[9]Tian Z,Zhang Z D,Ye Y D,et al.Analysis of real-time system conflict based on fuzzy time Petri nets[J].Journal of Intelligent & Fuzzy Systems:Applications in Engineering and Technology,2014,26(2):983-991.

[10]Popescu C,Soto M C,Lastra J L M.A Petri net-based approach to incremental modelling of flow and resources in service-oriented manufacturing systems[J].International Journal of Production Research,2012,50(2):325-343.

[11]Cheng A,et al.Complexity results for 1-safe nets[J].Theoretical Computer Science,1995,147(1-2):117-136.

[12]Esparza J.Reachability in live and safe free-choice Petri nets is NP-complete[J].Theoretical Computer Science,1998,198(1):211-224.

[13]Esparza J.Decidability and Complexity of Petri Net Problems—an Introduction[M].Berlin Heidelberg Springer:Lectures on Petri Nets I:Basic Models,1998:374-428.

[14]Jiang C.Polynomial-time algorithm for the legal firing sequences problem of a type of synchronous composition Petri nets[J].Science in China Series:Information Sciences,2001,44(3):226-233.

[15]Badouel E,Bernardinello L,Darondeau P.The synthesis problem for elementary net systems is NP-complete[J].Theoretical Computer Science,1997,186(1):107-134.

[16]潘理,赵卫东,王志成,等.Petri网的步问题研究[J].软件学报,2009,20(3):505-514.

Li Pan,Weidong Zhao,Zhicheng Wang.On the step problem for Petri nets[J].Journal of Software,2009,20(3):505-514 (in Chinese)

[17]Papadimitriou C H.Computational Complexity[M].Chichester:John Wiley and Sons Ltd.,2003.

[18]Garey M R,Johnson D S.Computers and Intractability[M].New York:W.H.Freeman & Co Ltd,2002.

[19]Bron C,Kerbosch J.Algorithm 457:finding all cliques of an undirected graph[J].Communications of the ACM,1973,16(9):575-577.

[20]Tomita E,Tanaka A,Takahashi H.The worst-case time complexity for generating all maximal cliques and computational experiments[J].Theoretical Computer Science,2006,363(1):28-42.

[21]潘理,丁志军,郭观七.混合语义时间Petri网模型[J].软件学报,2011,22(6):1199-1209.

Li Pan,Zhijun Ding,Guanqi Guo.Time Petri net model with mixed semantics[J].Journal of Software,2011,22(6):1199-1209.(in Chinese)

潘 理 男,1975年出生,湖南平江人.博士,湖南理工学院副教授.研究方向为Petri网、形式化建模与优化.

E-mail:panli.hnist@gmail.com

郑 红(通信作者) 女,1973年出生,博士,华东理工大学副教授,美国加州大学河滨分校访问学者.研究方向为普适计算、Petri网应用.

E-mail:zhenghong@ecust.edu.cn

Maximal Conflict Set Enumeration Algorithm Based on Locality of Petri Nets

PAN Li1,ZHENG Hong2,LIU Xian-ming3,YANG Bo1

(1.SchoolofInformationandCommunicationEngineering,HunanInstituteofScienceandTechnology,Yueyang，Hunan414006,China;2.InformationScienceandEngineeringCollege,EastChinaUniversityofScienceandTechnology,Shanghai,200237China;3.InformationandCommunicationBranch,JiangxiElectricPowerCompany,Nanchang,Jiangxi330077,China)

Conflict is an essential concept in Petri net theory.The existing research focuses on the modelling and resolution strategies of conflict problems,but less on the computational complexity of the problems theirselves.In this paper,we propose the conflict set problem for Petri nets,and prove that the conflict set problem is NP-complete.Furthermore,we present a dynamic algorithm for the maximal conflict set enumeration.Our algorithm only computes those conflict sets that are affected by local firing,which avoids enumerating all maximal conflict sets at each marking.The algorithm needs time O(m2n) where m is the number of maximal conflict sets at the current marking and n is the number of transitions.Finally,we show that the maximal conflict set enumeration problem can be solved in O(n2) for free-choice nets and asymmetric choice nets.The results on complexity of thel conflict set problem provide a theoretical reference for solving conflict problems of Petri nets.

Petri nets;conflict set problem;NP completeness;maximal conflict set enumeration algorithm

2015-05-12;

2015-11-09;责任编辑:马兰英

国家自然科学基金(No.61473118);湖南省教育厅科学研究重点项目(No.15A079);湖南省科技计划项目(No.2014GK3026);江西省电力公司科技项目(No.5218351400A1)

TP301

A

0372-2112 (2016)08-1858-06