陈 雷郑德忠廖文喆

（1. 燕山大学河北省测试计量技术及仪器重点实验室 秦皇岛 066004 2. 东北石油大学秦皇岛分校 秦皇岛 066004 3. 河北工业大学控制科学与工程学院 天津 300130）

基于压缩感知的含扰动电能质量信号压缩重构方法

陈 雷1,2郑德忠1廖文喆3

（1. 燕山大学河北省测试计量技术及仪器重点实验室 秦皇岛 066004 2. 东北石油大学秦皇岛分校 秦皇岛 066004 3. 河北工业大学控制科学与工程学院 天津 300130）

针对电能质量信号的压缩重构问题，提出了一种应用压缩感知理论对电能质量信号进行压缩采样和非线性恢复的方法。首先对含有扰动的电能质量信号的稀疏性和可压缩性进行了分析，并对现有的典型贪婪恢复算法的特性进行了研究，然后结合有代表性的SP和SAMP两种算法的优点，提出了一种改进的BSMP算法。应用包括BSMP在内的几种贪婪算法对含有谐波、间谐波、电压暂升和暂降等稳态和暂态扰动的电能质量信号的压缩重构性能进行仿真分析，仿真结果说明了BSMP算法恢复混合或单一扰动的电能质量信号的可行性。与现有贪婪算法相比，BSMP无需稀疏度先验，可以用较快的速度和更高的压缩比以100%的概率实现成功重构。

压缩感知 匹配追踪 重构算法 稀疏表示 电能质量

0 引言

传统的奈奎斯特（Nyquist）理论指出采样频率不能低于模拟信号频谱中最高频率的两倍。近几年提出的压缩感知理论，建立在信号稀疏表示和逼近理论基础上，打破了奈奎斯特理论的限制，是信号处理领域的一个新的研究方向。该理论指出，如果信号本身是稀疏或可压缩的，或者在某种变换域下是稀疏或可压缩的，则可以利用一种测量矩阵，将其投影到低维空间上，实现压缩采样。同时由于这种在低维空间上的投影采样包含了重构原始高维信号所需要的足够信息，因此可以使用非线性运算从低维空间上的少量采样测量值以高概率精确重构原始信号[1-4]。

电能质量是指电力系统公用电网供给的交流电能的品质。依据 IEEE 1159，电能质量问题主要包括电压和频率偏差、电压波动与闪变、三相不平衡、谐波和间谐波等稳态扰动，以及电压脉冲、振荡、中断、暂降和暂升等暂态扰动[5]。目前，随着工业化的迅速发展，电网电能质量问题变得越来越严峻，使其受到越来越多的关注，其研究范畴涉及去噪、压缩、检测、分类、评估和治理等几大方面[6]。由于实际电能质量信号的频率范围很宽，需要用较高的采样频率长时间不间断地采集，导致其数据量十分庞大，加重了数据存储和传输的负担，因此人们对电力信号数据压缩进行了大量研究，目前的研究大多是以小波理论为基础。文献[7,8]将基于小波或小波包变换系数的门限方法应用于电能质量检测数据的压缩，取得了一定的效果。文献[9,10]将小波与编码技术相结合，进一步提高了压缩效率。文献[11,12]引入二维小波实现压缩。文献[13]设计了一种基于模式相似性测度的电能质量信号压缩方法，其计算量远低于小波方法，但压缩比受频率波动影响较大，且可能丢失部分数据。以上压缩算法基本都是针对暂态或故障数据特征而设计的，且均建立在Nyquist定理基础上。必须先高速采样包含大量冗余信息的数据，然后丢弃大量的非重要数据实现压缩，造成了采样和存储资源的浪费。

如果利用压缩感知理论，可以用远低于Nyquist频率的采样率，直接采集到包含电能质量信号重要特征的少量采样值，实现数据采集和压缩的同步进行，从而大大降低采样、存储和传输的成本。本文在压缩感知理论下，对电能质量信号的压缩采样与重构问题进行研究，并在已有压缩感知重构算法的基础上提出了一种性能更好的算法，将其应用于含扰动电能质量信号的重构上，并对其进行了理论和仿真分析，证明了其有效性。

1 信号的稀疏性和可压缩性

信号的稀疏表示是压缩感知理论的基础和先决条件。考虑一种实值、有限长度的一维离散信号f∈RN，可看作具有N个元素的N×1维列向量。任何信号可以用N×1维基向量{ψi}, i=1,…,N的线性组合来表示，简化起见，假定基是正交的，使用N×N的基矩阵Ψ ={ψ1|ψ2|…|ψN}，其中{ψi}为矩阵的列，则信号f可表达为

这里x是N×1维的列向量，如果f是K个基向量的线性组合，K＜＜N，也就是式（1）中只有少量K个系数xi非零，其余N−K个系数为0，则称K是稀疏的；如果系数xi∈RN按一定量级呈现指数衰减，即只有少量K个大系数和大量小系数，则信号f是可压缩的，可以用这K个大系数很好地逼近[14,15]。

通常，变换基需要根据信号的特点来选取，常用的变换基主要有：离散余弦变换（Discrete Consine Transform, DCT）基、离散傅里叶变换（Discrete Fourier Transform, DFT）基、离散小波变换基、Curvelet基、Gabor基以及冗余字典等。

谱分析表明，含有谐波、间谐波稳态扰动的电能质量信号在傅里叶变换基下具有频域稀疏性，而对于含有电压暂升、暂降等暂态扰动的信号具有频域可压缩信号的性质。即电能质量扰动信号在合适的变换域下具有稀疏性或可压缩性。

2 压缩感知采样及重构原理

2.1稀疏信号的压缩感知问题

假设x∈RN是在时域只有K（K＜N）个非零元素的未知稀疏信号，u∈RM是x在M个非适应线性测量下的观测值，Φ =[ϕ1ϕ2… ϕM]T∈RM×N（M＜＜N, ϕi∈RN）为压缩感知中的压缩采样测量矩阵，M为测量维数，则有

压缩感知问题是通过M个压缩采样测量值u，通过非线性重构算法，恢复N维稀疏信号x的过程。

2.2变换域下稀疏信号的压缩感知问题

实际上，绝大多数自然信号本身在时域上并不稀疏，而是在某种变换域或者字典下是稀疏或可压缩的，如上节提到的电能质量信号。考虑一种通用的非适应线性测量过程

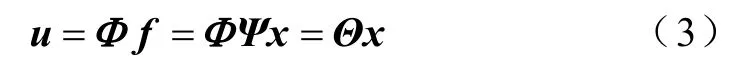
2.3压缩感知测量矩阵

对于式（3）的求解问题，由于M＜N，这个问题变成一个病态问题。然而，如果x中非零系数的K个位置已知，那么在K≤M的情况下，该问题有解的充要条件是：对于任意有K个非零项的向量x，满足

2.4压缩感知重构算法

根据以上论述，本节讨论变换域下稀疏或可压缩的电能质量信号的压缩感知求解问题。

最小l0范数等效于使求解得到的非零系数的个数最少，即信号最稀疏，因此求解式（3）的很自然的想法是在l0范数最小框架下求解

但求解式（5）是个完全的NP（non-deterministic polynomial）难问题，需要穷举 x中 K个非零项的所有种可能的位置。D. L. Donoho证明了l1范数为最接近l0范数的凸函数[17]，基于线性规划问题的l1范数最优化能够得到与l0范数同样的解。因此式（5）可以转化为如下求解l1范数最小问题。

这类算法称为l1-LP（liner program）重构算法，由于该类算法是求解全局最优解，所以算法具有极高的准确度和稳定性。主要有基追踪法、梯度投影法、内点法、迭代阈值法和迭代加权最小二乘法等。然而，l1-LP重构算法需要对其进行线性规划，计算量大，导致算法复杂度极高、速度很慢。因此，人们又提出了求取次最优解的基于贪婪迭代匹配追踪的系列算法，该系列算法是通过逐步选取对压缩测量值产生最大影响的列向量来实现对原始信号的最优估计。目前主要有：MP、OMP、StOMP、ROMP、SP、CoSaMP和SAMP等算法[18-21]。除了以上两大类算法外，还有贝叶斯类算法和组合算法等。

3 后向子空间匹配追踪重构算法

由于贪婪匹配追踪类算法结构简单、速度快且更具实用性，因此本文通过研究现有一系列贪婪算法，结合几种算法的优点，提出了一种后向子空间匹配追踪（Backward Subspace Matching Pursuit, BSMP）算法。

基于迭代贪婪追踪思想的早期算法是 MP和OMP，后来又出现了分段正交匹配追踪 StOMP算法和正则化正交匹配追踪ROMP，这些算法的重构复杂度为O（KMN），要比l1-LP类算法低得多。但要实现精确重构，需要更多的测量值，并且不能保证重构质量。因此一些基于回溯思想的贪婪算法被提出来，有代表性的是子空间追踪 SP和压缩采样匹配追踪CoSaMP，它们提供了类似l1-LP方法的重构质量的理论保证以及更低的重构复杂度。SP和CoSaMP算法并不像 OMP类算法那样每次迭代选出Θ中的一个或几个列向量，而是在第一次迭代就选出Θ中的K个列向量，然后通过继续迭代，不断优化这K个列向量，进而得到最优的向量集合，用来重构信号。

但是，SP和CoSaMP都假定稀疏度K为已知，因此，需要预先估计K值。文献[21]通过实验证明，如果低估了K值，会导致算法不能精确恢复信号，如果K值估计过高，会大幅度降低算法的重构准确度和鲁棒性。可见，如果K的估计与真值相差太远，SP算法的性能降低很快，CoSaMP算法也有类似的情况。鉴于此，文献[21]提出的稀疏自适应匹配追踪算法SAMP，可以处理稀疏度K未知的信号，提供了基于最优化方法的理论保证，并且具有比以上算法更优秀的重构性能。

本文结合 SP和 CoSaMP算法的回溯思想和SAMP的稀疏度自适应思想，在 SP算法基础上进行改进，提出一种采用回溯思想和盲稀疏度估计的BSMP算法，并将其应用到电能质量信号的重构中。为了说明该算法，首先对 SP算法的思想及实现方法进行简要介绍如下：

（1）输入：Θ，u，稀疏度估计K。

SP算法的特点是，在稀疏度K估计较准确的情况下效率很高，该算法每次迭代，通过执行删除步骤进行回退筛选，使整个迭代一直保留着长度为 K的支撑估计集，通过几次迭代即可得到稀疏解向量。

SP算法基于迭代扩展和收缩支撑集合，从而允许在支撑估计中添加和删除错选的非零索引。但是，需要预先估计稀疏度 K，使支撑大小在迭代过程中保持不变，这对于大多数实际应用是个障碍。

BSMP算法采用 SP的通过回溯迭代扩展和收缩支撑集合，并吸收SAMP的按照指定步长扩展支撑，进而实现稀疏自适应的思想，在不需要稀疏度先验估计的情况下，实现重构。该算法的实现步骤如下：

（1）输入：Θ，u，前向步长L1，后向步长L2。

④ 将xp后L2个幅值最小项的坐标存入集合I2，即中幅值最小的L2个元素的索引}。

⑦ 满足循环条件，则重复执行步骤①～⑥，否则跳出循环，并输出解向量

BSMP算法的迭代过程可描述如下：

电能质量扰动复杂多样，其稀疏度无法预先确定，BSMP综合了SP的高效性和SAMP不需要稀疏先验的优点，无需预先估计电能质量信号的稀疏度K，每次迭代，按步长扩展支撑集，这样反复迭代，直到观测向量的残差能量不满足循环条件或迭代次数达到指定的最大次数Km，即可得到稀疏解向量x，进而可用稀疏基重构电能质量信号。

4 仿真分析

4.1重构性能指标

相对方均根误差（Relative Root Mean Square Error, RRMSE），简称相对误差，其表达式为

重构信噪比（Signal to Noise Ratio, SNR）为

压缩比（Compression Ratio, CR）为

4.2重构成功条件

4.3仿真

Ψ 采用正交傅里叶变换基，每次随机产生新的高斯分布测量矩阵Φ。对于 BSMP算法，参考文献[22]中所述的方法，同时通过大量仿真得到，当取前向步长约为后向步长即扩展步长为2，可以兼顾不同M下的恢复性能与运算速度；同样，对于SAMP算法中的步长取2。

4.3.1含有谐波扰动的重构

设电能质量测试信号中含有3次、5次和7次谐波扰动，所用信号模型为

采样率1.6kHz，原始信号长度N=1 600，谱分析可知，其傅里叶正交基下的稀疏度为8。

假设信号的实际稀疏度未知，这里稀疏度估计为K=10和20，分别进行仿真分析。并对每个M重复100次仿真，计算成功重构概率。图1a和图1b分别给出了K=10和K=20时的成功重构概率曲线，x轴代表测量值M，y轴代表成功重构的概率。可见相同的M下，BSMP实现了相对更高的重构概率，SP和CoSaMP的稀疏度估计与实际值相差越大，重构性能越差。根据图1b，可以得到表1，即100%成功重构时，各种算法的最小M值及其对应的压缩比CR。表2给出了K=20、M=80，成功重构概率均为100%时，各种算法的平均运行时间。

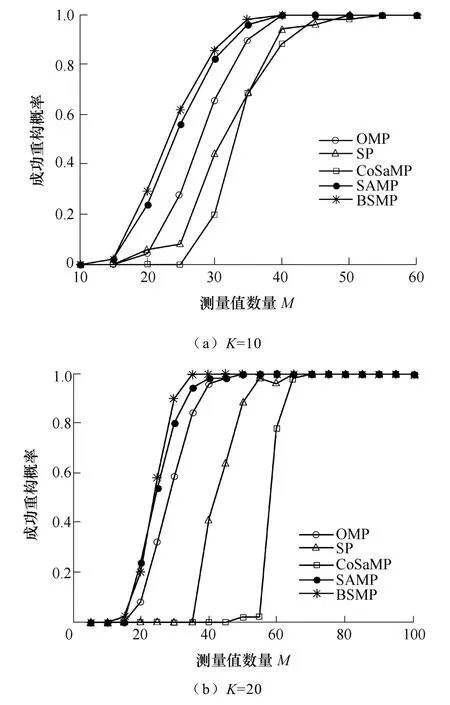
图1　含有谐波稳态扰动的电能质量信号在不同算法下的成功重构概率与M的关系Fig.1 Probability of successful recovery of power quality signal with harmonic vs the number of measurements M under different algorithms

表1　不同算法下的重构压缩比（N=1 600 K=20）Tab.1 Compression ratio of each algorithm

表2　不同算法的平均运行时间（N=1 600 M=80 K=20）Tab.2 Average run time of each algorithm

整体而言，BSMP算法无需估计稀疏度，且与SAMP算法相比具有时间优势，同时可用较少的压缩采样值，以更高的压缩比实现重构。

4.3.2含有谐波、间谐波扰动的重构

设电能信号包含有3次、5次、7次和11次谐波，间谐波频率有72Hz、120Hz、453Hz和511Hz，表达式为

采样率1.6kHz，信号长度N=1 600，其傅里叶正交基下的稀疏度为18。

这里取稀疏度估计值K=30，对应每个M值重复仿真 100次，计算成功重构的概率，得到如图 2所示的曲线。可见，相同的M取值下，BSMP、SAMP算法的成功重构概率最高，OMP次之，SP、CoSaMP性能较差。表 2给出了K=30，M=120时几种算法的平均运行时间。综合图 2和表 3，可见，BSMP算法的综合重构性能最好。

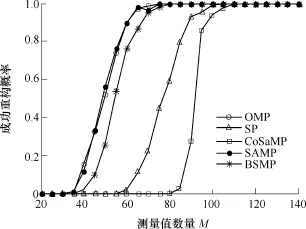
图2　含有谐波、间谐波稳态扰动的电能质量信号在不同算法下的成功重构概率与M的关系Fig.2 Probability of successful recovery of power quality signal with harmonic and interharmonic vs the number of measurements M under different algorithms

表3　不同算法的平均运行时间（N=1 600 M=120 K=30）Tab.3 Average run time of each algorithm

4.3.3稀疏基下的可压缩电能质量信号的重构

含有电压中断、暂升、暂降和振荡等暂态扰动的电能质量信号，在傅里叶变换基下具有可压缩性。由于可压缩信号的稀疏度更加难于估计，因此这里仅对具有稀疏度自适应的BSMP和SAMP两种算法进行对比仿真，对应每个M值重复仿真100次，计算成功重构概率，仍取N=1 600，采样率1.6kHz。各种扰动组合的种类复杂多样，这里考虑包含如下两种典型扰动信号的重构，设信号在 1 000～1 280的采样点处产生幅度为20%的暂升或暂降，对应的时间是t1～t2。

1）对于只包含有电压暂升的单一扰动的电能质量信号，所用信号模型为

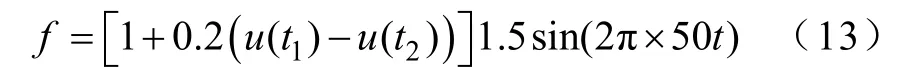
成功重构的概率曲线如图3所示，图中，BSMP 和SAMP两种算法的重构概率曲线基本一致。

图3　含有电压暂升扰动的成功重构概率对比Fig.3 Probability of successful recovery with voltage swell

取M=140时，即压缩比为11∶1时，两种算法成功重构概率均为100%，仿真得到，BSMP的平均运行时间约为130ms，而SAMP约为420ms；BSMP下运行100次的RRMSE平均值为0.025，重构信号的SNR平均值为32dB，与SAMP基本一致。图4给出了BSMP算法下，M=140时，原始信号（见式（13））、重构信号及重构误差的波形。

图4　基于BSMP的含电压暂升扰动重构波形Fig.4 Reconstruction waveforms with voltage swell using BSMP

2）对于同时含有谐波、间谐波和电压暂降的复合扰动电能质量信号，所用信号模型为

成功重构概率曲线如图5所示，BSMP和SAMP两种算法的重构概率曲线也是基本一致的。取M= 160时，即压缩比为10∶1时，BSMP的平均运行时间约为210ms，SAMP约为475ms；BSMP下运行100次的RRMSE平均值为0.033，重构信号的SNR平均值为30dB，与SAMP基本一致。图6给出了BSMP算法下，M=160时，原始信号式（14）、重构信号及重构误差的波形。

图5　含有复合扰动的成功重构概率对比Fig.5 Probability of successful recovery with mixed disturbances

图6　基于BSMP的含复合扰动重构波形Fig.6 Reconstruction waveforms with mixed disturbances using BSMP

以上采用BSMP和SAMP两种算法对信号式（13）和式（14）的重构仿真表明，相同重构条件下两种算法的重构概率曲线和重构指标基本一致，但BSMP算法的速度更快。

进一步实验得到，适当减小压缩比，可以进一步减小RRMSE，并提高SNR。当取M=400，即压缩比减小到4∶1时，BSMP算法下，分别对式（13）和式（14）所示信号进行压缩感知重构，运行 100次，得到RRMSE的平均值分别为0.015和0.018，SNR平均值分别为36.2dB和34.8dB，即通过牺牲压缩比，获得重构性能的提升。另外，如果在确保成功重构的压缩比下，适当增加扩展步长，还可以进一步缩短BSMP算法的运行时间。

5 结论

将压缩感知引入到电能质量信号的压缩重构领域。对含有稳态和暂态扰动的电能质量信号的稀疏性和可压缩性进行了分析，在压缩感知理论下实现对电能质量信号的压缩采样，并采用贪婪算法进行非线性重构。仿真分析表明，所提出的BSMP贪婪算法可以在稀疏度未知的情况下，以更少的测量值，获得比现有贪婪算法更好的重建效果，并且运行时间低于同样具有盲稀疏度恢复的SAMP算法。理论分析和仿真结果表明，该方法信号重建速度较快，重构效果更好，适合含扰动电能质量信号的压缩感知重构应用。

[1] Donoho D. Compressed sensing[J]. IEEE Transactions on Information Theory, 2006, 52(4): 1289 1306.

[2] Baraniuk R. Compressive sensing[J]. IEEE Signal Processing Magazine, 2007, 24(4): 118-121.

[3] 焦李成, 杨淑媛, 刘芳, 等. 压缩感知回顾与展望[J]. 电子学报, 2011, 39(7): 1651-1662. Jiao Licheng, Yang Shuyuan, Liu Fang, et al. Development and prospect of compressive sensing[J]. Acta Electronica Sinica, 2011, 39(7): 1651-1662.

[4] 李树涛, 魏丹. 压缩传感综述[J]. 自动化学报, 2009, 35(11): 1369-1377. Li Shutao, Wei Dan. A survey on compressive sensing[J]. Acta Automatic Sinica, 2009, 35(11): 1369-1377.

[5] IEEE Power & Energy Society. IEEE standard 1159—2009: IEEE recommended practice for monitoring electric power quality[S]. 2009.

[6] 程浩忠, 吕干云, 周荔丹. 电能质量监测与分析[M]. 北京: 科学出版社, 2012.

[7] 欧阳森, 宋政湘, 陈德桂, 等. 基于小波原理的电能质量检测数据实时压缩方法[J]. 电网技术, 2003, 27(2): 37-40. Ouyang Sen, Song Zhengxiang, Chen Degui, et al. A wavelet theory based real-time data compression method for power quality detection[J]. Power System Technology, 2003, 27(2): 37-40.

[8] 郭彬彬, 黄纯. 基于小波包变换的电能质量扰动数据压缩[J]. 电力自动化设备, 2005, 25(11): 34-37. Guo Binbin, Huang Chun. Power quality disturbance data compression based on wavelet packet transform[J]. Electric Power Automation Equipment, 2005, 25(11): 34-37.

[9] 王成山, 王继东. 基于能量阈值和自适应算术编码的数据压缩方法[J]. 电力系统自动化, 2004, 28(24): 56-60. Wang Chengshan, Wang Jidong. Data compression method based on energy threshold and adaptive arithmetic encoding[J]. Automation of Electric Power Systems, 2004, 28(24): 56-60.

[10] 朱永利, 翟学明, 姜小磊. 绝缘子泄漏电流的自适应SPIHT 数据压缩[J]. 电工技术学报, 2011, 26(12):190-196. Zhu Yongli, Zhai Xueming, Jiang Xiaolei. Adaptive SPIHT algorithm for data compression of insulator leakage currents[J]. Transactions of China Electrotechnical Society, 2011, 26(12): 190-196.

[11] 鲍文, 周瑞, 刘金福. 基于二维提升小波的火电厂周期性数据压缩算法[J].中国电机工程学报, 2007, 27(29): 96-101. Bao Wen, Zhou Rui, Liu Jinfu. A periodical data compression method based on 2-D lifting wavelet transform in thermal power plant[J]. Proceedings of the CSEE, 2007, 27(29): 96-101.

[12] 刘毅, 周雒维, 冯浩. 电能质量监测网录波数据压缩方法[J]. 电网技术, 2010, 34(4): 199-203. Liu Yi, Zhou Luowei, Feng Hao. Method for compressing recorded data from power quality monitoring network[J]. Power System Technology, 2010, 34(4): 199-203.

[13] 黄南天, 徐殿国, 刘晓胜, 等. 基于模式相似性测度的电能质量数据压缩方法[J]. 电工技术学报, 2011, 26(10): 39-46, 61. Huang Nantian, Xu Dianguo, Liu Xiaosheng, et al. Power quality data compression based on pattern similarity measurement[J]. Transactions of China Electrotechnical Society, 2011, 26(10): 39-46, 61.

[14] Cohen A, Dahmen W, DeVore R. Compressed sensing and best k-term approximation[J]. Journal of the American Mathematical Society, 2009, 22(1): 211-231.

[15] Boufounos P, Kutyniok G, Rauhut H. Sparse recovery from combined fusion frame measurements[J]. IEEE Transactions on Information Theory, 2011, 57(6): 3864-3876.

[16] Candès E. The restricted isometry property and its implications for compressed sensing[J]. Comptes Rendus Mathematique, 2008, 346 (9-10): 589-592.

[17] Donoho D L. For most large underdeterminedsystems of linear equations the minimal l1-norm solution is also the sparsest solution[J]. Communications on Pure and Applied Mathematics, 2006, 59(6): 797- 829.

[18] 杨真真, 杨震, 孙林慧. 信号压缩重构的正交匹配追踪类算法综述[J]. 信号处理, 2013, 29(4): 486-496. Yang Zhenzhen, Yang Zhen, Sun Linhui. A survey on orthogonal matching pursuit type algorithms for signal compression and reconstruction[J]. Signal Processing, 2013, 29(4): 486-496.

[19] Dai W, Milenkovic O. Subspace pursuit for compressive sensing signal reconstruction[J]. IEEE Transactions on Information Theory, 2009, 55(5): 2230-2249.

[20] Needell D, Tropp J A. CoSaMP: iterative signal recovery from incomplete and inaccurate samples[J]. Communications of the ACM, 2010, 53(12): 93-100.

[21] Do T T, Gan L, Nguyen N, et al. Sparsity adaptive matching pursuit algorithm for practical compressed sensing[C]//Asilomar Conference on Signals, Systems, and Computers, Pacific Grove, California, 2008, 10: 581-587.

[22] Maleki A, Donoho D L. Optimally tuned iterative reconstruction algorithms for compressed sensing[J]. IEEE Journal of Selected Topics in Signal Processing, 2009, 4(2): 330-341.

Method Based on Compressed Sensing for Compression and Reconstruction of Power Quality Signals with Disturbances

Chen Lei1,2Zheng Dezhong1Liao Wenzhe3
（1. Key Laboratory of Measurement Technology and Instrumentation of Hebei Province Yanshan University Qinhuangdao 066004 China 2. Northeast Petroleum University at Qinhuangdao Qinhuangdao 066004 China 3. College of Control Science and Engineering Hebei University of Technology Tianjin 300130 China）

A method based on compressed sensing theory is proposed to realize the compressive sampling and nonlinear recovery. The compressibility and the sparsity of the disturbed power quality signals are analyzed, and the existing iterative greedy pursuit recovery algorithms are reviewed. Combined with the advantages of two typical algorithms SP and SAMP, an improved method named BSMP is proposed. Then the reconstruction performance of several typical greedy pursuit recovery algorithms are simulated and analyzed, using the power quality signals with steady or transient disturbances such as harmonics, interharmonics, voltage swell and sag, etc. Results verify the feasibility of the BSMP in recovering the power quality signals with mixed or single disturbances. Compared with the existing greedy algorithms, BSMP algorithm does not require sparsity level as prior information, and can realize the successful reconstruction absolutely with faster speed and higher compression ratio.

Compressed sensing, matching pursuit, reconstruction algorithm, sparse representation, power quality

TM74

陈 雷 男，1979年生，博士研究生，副教授，研究方向为电能质量分析、智能检测与信号。

E-mail: addisonqhd@163.com（通信作者）

郑德忠 男，1949年生，教授，博士生导师，研究方向为系统仿真、信号处理、遥测遥控和先进控制等。

E-mail: lianxiangqhd@126.com

河北省自然科学基金（F2014203224）和秦皇岛市科技支撑计划（201302A042）资助项目。

2014-04-28 改稿日期 2015-01-06