张春霞,翟晓蕊

(西北师范大学数学与统计学院,甘肃兰州　730070)



复形的Cartan-Eilenberg Gorenstein投射维数

张春霞,翟晓蕊

(西北师范大学数学与统计学院,甘肃兰州730070)

定义了Cartan-Eilenberg(CE) Gorenstein合冲复形,证明了对任意正整数n,复形K是CE Gorensteinn-合冲复形当且仅当它是CEn-合冲复形；给出了复形的CE Gorenstein投射维数的等价刻画.作为应用,证明了具有有限CE Gorenstein投射维数的复形存在CE Gorenstein投射预覆盖.

CE Gorenstein 投射复形;CE Gorenstein 投射维数;CE Gorensteinn-合冲复形;CEn-合冲复形

0　引言

1997年,Verdier[1]给出了Cartan-Eilenberg(CE)内射复形和CE投射复形的概念,并引入了复形的CE内射分解和CE投射分解.2011年,Enochs[2]介绍了CE Gorenstein内射复形,证明了任意的CE Gorenstein内射复形都可由完全CE内射分解得到.2014年,Yang-Liang[3]研究了与内射对偶的CE Gorenstein投射复形,给出了复形的CE Gorenstein投射维数的一些同调刻画.

受以上文献启发,本文对复形的CE Gorenstein 投射维数进行探究.借助Huang[4]研究Gorenstein合冲和维数的方法,我们首先定义CE Gorenstein合冲复形,证明了对任意正整数n,复形K是CE Gorensteinn-合冲复形当且仅当它是CEn-合冲复形；然后，我们给出了复形的CE Gorenstein投射维数的等价刻画,即对任意非负整数n及复形C,CE-Gpd(C)≤n当且仅当对任意一个整数t:0≤t≤n,存在CE正合序列

使得Gt是CE Gorenstein投射复形,Gi是CE 投射复形(i≠t)；作为应用,证明了具有有限CE Gorenstein投射维数的复形存在CE Gorenstein投射预覆盖.

1　预备知识

除非特别申明,本文中的环R是指具有单位元的结合环,模均指酉R-模,复形均指R-复形.

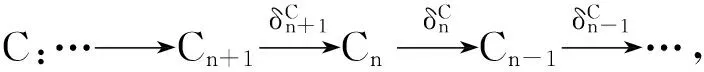
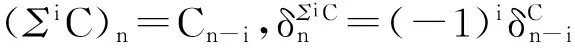
设F是任意R-模类,将每个层次的模均在F中的复形所构成的类记为C(F).

定义1[2]设F是一个R-模类,称复形A为CEF复形,如果A,Z(A),B(A),H(A)都属于C(F1).将所有CE F复形构成的类记为CE(F).

特别地,若F是投射(或内射,Gorenstein投射,Gorenstein内射)R-模类,则CE F复形就是CE投射(或内射,Gorenstein投射,Gorenstein内射)复形.

定义2[2]称R-复形序列…→C1→C0→C-1→…是CE正合的,如果以下序列均为正合序列:

( i )…→C1→C0→C-1→…;

( ii )…→Z(C1)→Z(C0)→Z(C-1)→…;

(iii)…→B(C1)→B(C0)→B(C-1)→…;

(iv)…→C1/Z(C1)→C0/Z(C0)→

C-1/Z(C-1)→…;

( v )…→C1/B(C1)→C0/B(C0)→

C-1/B(C-1)→…;

(vi)…→H(C1)→H(C0)→H(C-1)→….

注1：由文献[5]引理9.2.2可知,在上述序列中,若(i)与(ii)或(i)与(v)正合,则(i)～(vi)都正合.

命题1设F是一个R-模类.对R-复形的正合序列C:…→C1→C0→C-1→…，以下结论成立:

( i )若Hom(CE(F),C)正合,且F包含一个忠实投射R-模,则C是CE正合的.特别地,若C是短正合序列,且C1为正合复形,则C是CE正合的.

( ii )若Hom(C,CE(F))正合,且F包含一个忠实内射R-模,则C是CE正合的.

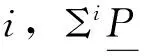
(1)

由文献[2]命题2.1(1)可得正合序列

(2)

所以…→Z(C1)→Z(C0)→Z(C-1)→…是正合序列.由注1可知C是CE正合的.

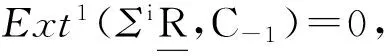
(ii)证明过程与(1)类似,由文献[2]命题2.1(2)和注1可知C是CE正合的.】

定义3[3]R-复形G的完全CE投射分解是指由CE投射复形构成的CE正合序列P:…→P1→P0→P-1→…,使得G≅Ker(P0→P-1),并且对任意CE投射复形Q,Hom(P,Q)是正合的.

命题2[3]对R-复形G,以下条件等价:

( i )B(G),H(G)∈C(GP(R));

(ii)G,G/B(G)∈C(GP(R));

(iii)G有完全CE投射分解;

(iv)G是CE Gorenstein投射复形.

定义4[4]称R-复形C的CE Gorenstein投射维数小于或等于n,记为CE-Gpd(C)≤n,如果存在CE正合序列0→Gn→Gn-1→…→G0→C→0,使得每个Gi是CE Gorenstein投射复形.若n是满足上述CE正合序列的最小非负整数,则记CE-Gpd(C)=n;若n不存在,则记CE-Gpd(C)=∞.

2　复形的CE Gorenstein投射维数

引理1设R-复形序列0→A→B→C→0是CE正合的.若其中任意两个复形有有限的CEGorenstein投射维数,则第三个复形也有有限的CEGorenstein投射维数.

证明由CE正合序列的定义可知,对任意整数i,存在以下正合序列:

(3)

(4)

设复形A,B有有限的CEGorenstein投射维数,则存在非负整数n,使得CE-Gpd(A)≤n,CE-Gpd(B)≤n,于是由文献[3]命题2.15可知:Gpd(Bi(A))≤n,Gpd(Hi(A))≤n,Gpd(Bi(B))≤n,Gpd(Hi(B))≤n.由文献[7]定理2.24及(3)和(4)式可知Gpd(Bi(C))<∞,Gpd(Hi(C))<∞.再根据文献[3]命题2.15可得CE-Gpd(C)<∞,即复形C的CEGorenstein投射维数有限.

对其它情形,同理可证.】

命题3设R-复形序列0→A→B→C→0是CE正合的且A≠0.若C是CEGorenstein投射复形,则CE-Gpd(A)=CE-Gpd(B).

证明由文献[3]命题2.14和引理1可得.

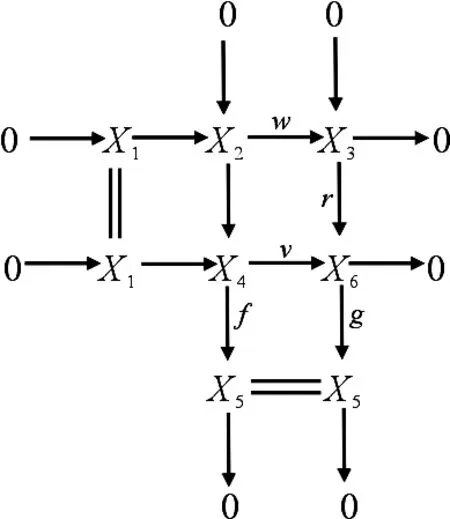
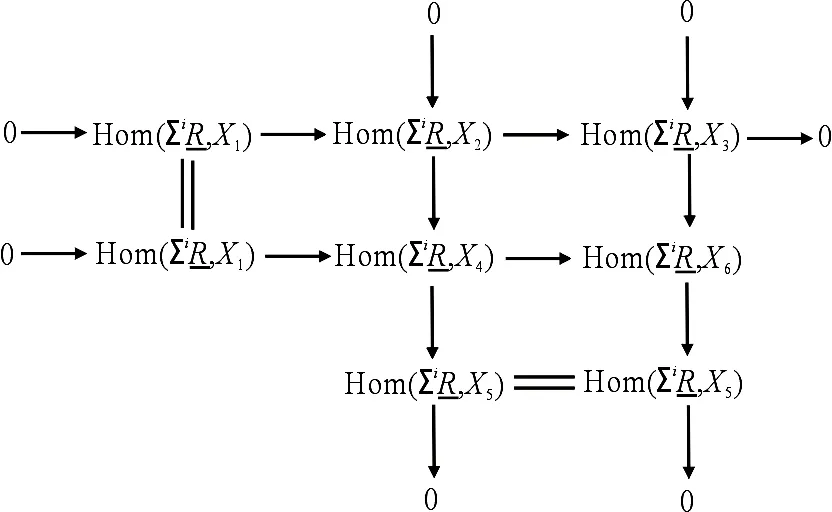
引理2由复形范畴中的两个CE短正合序列构成的推出图或拉回图中,所有的行和列都是CE正合的.

证明设有关于X2→X3和X2→X4的推出图

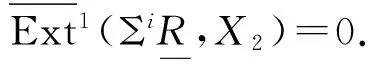
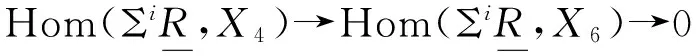
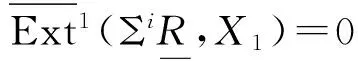
命题4设R-复形序列0→L→G1→G0→C→0是CE正合的,其中G1,G0是CE Gorenstein投射复形,则存在CE正合序列:

其中P,Q是CE投射复形,G,H是CE Gorenstein投射复形.

证明令M=Im(G1→G0),则有两个CE短正合序列:

因为G1是CE Gorenstein投射复形,所以由命题2知，存在CE正合序列0→G1→P→G2→0,使得P是CE投射复形,G2是CE Gorenstein投射复形，所以有如下推出图:

再考虑推出图

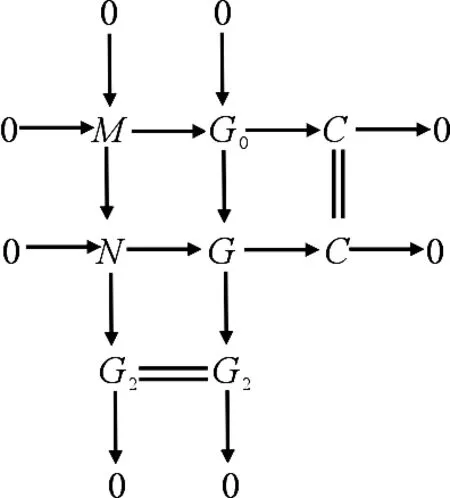
在CE正合序列0→G0→G→G2→0中,因为G0,G2都是CE Gorenstein投射复形,所以由命题3知G也是CE Gorenstein投射复形.由推出图中两个CE短正合序列0→L→P→N→0和0→N→G→C→0可得CE正合序列0→L→P→G→C→0,其中P是CE投射复形,G是CE Gorenstein投射复形.

因为G0是CE Gorenstein投射复形,所以由命题2知存在CE正合序列0→G3→Q→G0→0,使得Q是CE投射复形,G3是CE Gorenstein投射复形.对偶于上面的证法,做两个拉回图即可得到CE正合序列0→L→H→Q→C→0,其中Q是CE投射复形,H是CE Gorenstein投射复形.】

定义5对任意的正整数n,称R-复形K为复形C的CEn-合冲复形(或CE Gorensteinn-合冲复形),若存在CE正合序列0→K→Gn-1→Gn-2→…→G0→C→0,使得每个Gi是CE(或CE Gorenstein)投射复形.

注2：若R-复形K是复形C的CEn-合冲复形(或CE Gorensteinn-合冲复形),则由定义5可知,对任意整数i,Ki(或Zi(K),Bi(K),Hi(K))是Ci(或Zi(C),Bi(C),Hi(C))的n-合冲(或Gorensteinn-合冲).

定理1对任意正整数n及CE正合序列0→K→Gn-1→Gn-2→…→G0→C→0,若每个Gi是CE Gorenstein投射复形,则以下结论成立:

( i )存在CE正合序列0→K→Pn-1→Pn-2→…→P0→T→0和0→C→T→G→0,使得每个Pi是CE投射复形,G是CE Gorenstein投射复形.

( ii )存在CE正合序列0→L→Qn-1→Qn-2→…→Q0→C→0和0→H→L→K→0,使得每个Qi是CE投射复形,H是CE Gorenstein投射复形.

证明由于(ii)的证明与(i)对偶,此处只给出(i)的证明.设n≥1,对n进行数学归纳.

当n=1时,有CE正合序列0→K→G0→C→0.因为G0是CE Gorenstein投射复形,所以由命题2知,存在CE正合序列0→G0→P0→G→0,使得P0是CE投射复形,G是CE Gorenstein投射复形.于是依如下推出图即可获证：

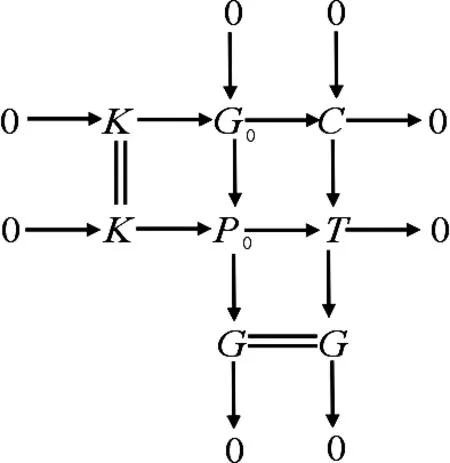
(5)

由归纳假设知存在以下两个CE正合序列:

(6)

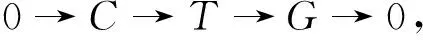
(7)

使得每个Pi是CE投射复形,G是CE Gorenstein投射复形.

结合由(5)～(7)式结论即可得证.】

推论1对任意正整数n,R-复形K是CE Gorensteinn-合冲复形当且仅当它是CEn-合冲复形.

证明由定理1(i)和定义5可得.】

推论2([3, 命题2.1.9])设R-复形C的CE Gorenstein投射维数有限,则存在CE正合序列0→C→T→G→0,使得G是CE Gorenstein投射复形,且CE-pd(T)=CE-Gpd(C).

证明设CE-Gpd(C)= n<∞，则由定理1中K=0的结论可得CE正合序列0→C→T→G→0,使得G是CEGorenstein投射复形,且CE-pd(T)≤n.再根据命题3知CE-Gpd(T)=CE-Gpd(C)=n.因为每个CE投射复形都是CEGorenstein投射复形,所以CE-Gpd(T)≤CE-pd(T)恒成立.由此可得CE-pd(T)=n.】

定理2设C是R-复形,则对任意非负整数n,以下条件等价:

( i )CE-Gpd(C)≤n.

( ii )对任意一个非负整数t:0≤t≤n,存在CE正合序列0→Gn→Gn-1→…→G0→C→0,使得Gt是CE Gorenstein投射复形,Gi是CE投射复形(i≠t).

证明(ii)⟹(i)显然.

(i)⟹(ii).对n进行数学归纳.

当CE-Gpd(C)≤1时,由定义4知存在CE正合序列0→C1→C0→C→0且C1,C0是CEGorenstein投射复形.由命题4中L=0的结论可得两个CE正合序列:

其中P1,P0是CE投射复形,G1,G0是CEGorenstein投射复形.

现只需要证明t=0的情形.令M=Im(C1→C0),可得到CE正合序列0→Cn→Cn-1→…→C1→M→0,显然CE-Gpd(M)≤n-1.由归纳假设知存在CE正合序列0→Pn→Pn-1→…→P2→G1→M→0,使得G1是CEGorenstein投射复形,Pi是CE投射复形,i=2,3,…,n.令K=Im(P2→G1),根据命题4,由CE正合序列0→K→G1→C0→C→0可得到CE正合序列0→K→P1→G0→C→0,其中P1是CE投射复形,G0是CEGorenstein投射复形.因此存在CE正合序列0→Pn→Pn-1→…→P1→G0→C→0,使得G0是CEGorenstein投射复形,Pi是CE投射复形,i=1,2,…,n.】

推论3([3,定理2.18])设C是R-复形,且CE-Gpd(C)=n,则存在CE正合序列0→K→G0→C→0,使得G0→C是C的CE Gorenstein投射预覆盖,且CE-pd(K)=n-1(若n=0,则K=0).

证明设CE-Gpd(C)=n≤∞.由定理2中t=0的结论可得到CE正合序列0→Pn→Pn-1→…→P1→G0→C→0,使得G0是CEGorenstein投射复形,Pi是CE投射复形,i=1,2,…,n.令K=Im(P1→G0),则有CE正合序列0→K→G0→C→0,且CE-pd(K)≤n-1.类似于引理1的证明,由文献[7]命题2.18和文献[3]命题2.15可知CE-Gpd(K)=n-1.因为每个CE投射复形都是CEGorenstein投射复形,所以CE-Gpd(K)≤CE-pd(K)恒成立.由此可得CE-pd(K)=n-1.

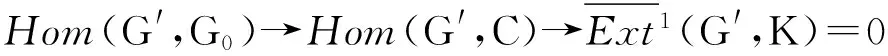
[1]VERDIERJL.Descategoriesderiveesdescategoriesabeliennes[J].Asterisque,1996,239:227.

[2]ENOCHSEE.Cartan-Eilenbergcomplexesandresolution[J].J Algebra,2011,342:16.

[3]YANGG,LIANGL.Cartan-EilenbergGorensteinprojectivecomplexes[J].J Algebra Appl,2014,13:1350068.

[4]HUANGCH,HUANGZY.Gorensteisyzygymodules[J].J Algebra,2010,324:3408.

[5]ENOCHSEE,JENDAOMG.Relative Homological Algebra[M].DeGruyterExpositionsinMathematicsVol.54.NewYork:DeGruyter,2011.

[6]GILLESPIEJ.TheflatmodelstructureonCh(R)[J].Trans Amer Math Soc,2004,356:3369.

[7]HOLMH.Gorensteinhomologicaldimensions[J].J Pure Appl Algebra,2004,189:167.

(责任编辑马宇鸿)

Cartan-Eilenberg Gorenstein projective dimension of complexes

ZHANG Chun-Xia,ZHAI Xiao-rui

(College of Mathematics and Statistics,Northwest Normal University,Lanzhou 730070,Gansu,China)

After introducing the concept of Cartan-Eilenberg(CE) Gorenstein syzygy complexes,it is proved that a complexKis CE Gorensteinn-syzygy complex if and only if it is a CEn-syzygy complex for any positive integern.Furthermore,an equivalent characterization of CE Gorenstein projective dimension of complexes is given.As applications,it is proved that a complex existing finite CE Gorenstein projective dimension has a CE Gorenstein projective precover.

CE Gorenstein projective complex;CE Gorenstein projective dimension;CE Gorensteinn-syzygy complex;CEn-syzygy complex

10.16783/j.cnki.nwnuz.2016.03.001

2014-12-24;修改稿收到日期:2015-12-24

国家自然科学基金资助项目(11261050,11401475)

张春霞(1979—),女,甘肃庆阳人,副教授,博士，硕士研究生导师.主要研究方向为同调代数理论.

E-mail:zhangcx@nwnu.edu.cn

O 153.3

A

1001-988Ⅹ(2016)03-0001-05