郭金运，徐晓飞，沈　毅

(山东科技大学 测绘科学与工程学院，山东 青岛 266590)



整体最小二乘算法及测量应用研究综述

郭金运，徐晓飞，沈毅

(山东科技大学 测绘科学与工程学院，山东 青岛 266590)

摘要：近30年来整体最小二乘法(TLS)被广泛应用于通信、大地测量与摄影测量以及图像处理等领域，成为测量数据处理的新方法。本文根据整体最小二乘法的基本思想，分析了基于奇异值分解与拉格朗日逼近的解算方法，总结归纳了加权整体最小二乘、混合整体最小二乘、带有约束的整体最小二乘以及病态情形下的整体最小二乘解算方法，综述了整体最小二乘在测绘领域的应用,补充了测量数据处理理论研究。

关键词：整体最小二乘；EIV模型；系数矩阵；奇异值分解；数据处理

最小二乘法(Least Squares，LS)是经典测量数据处理中最基本方法，该方法仅考虑观测量的偶然误差，可以得出最优一致无偏估计[1]。在实际测量数据处理中，不仅观测向量具有相应的随机模型，而且系数矩阵也常常含有误差，这种情况下使用LS得到的解是不准确的。因此，如何解决观测量与系数矩阵同时存在误差的问题，是测量数据处理领域的难点之一。目前，处理这类问题最常用的方法是整体最小二乘法(Total Least Squares，TLS)。

TLS是近30年发展起来的能解决观测量与系数矩阵同时存在误差的一种数据处理方法。Gloub与Van Loan[2]于1980年在数值分析领域提出TLS的概念。基于奇异值分解，他们对这个问题进行了分析，并设计了相应算法。尽管在测量领域进行TLS研究是从20世纪90年代开始的，但是结合本领域实际测量问题也获得了十分丰富的研究成果[3]。

本文总结和分析整体最小二乘法及其解算方法，归纳其在测量实际中的应用，并对今后整体最小二乘法在测量中的应用做了进一步展望。

1经典TLS问题及其解算方法

一个简单的随机误差EIV(Error-In-Variable)模型[4]可定义为：

函数模型：

L=(A-EA)X+el；

(1)

随机模型：

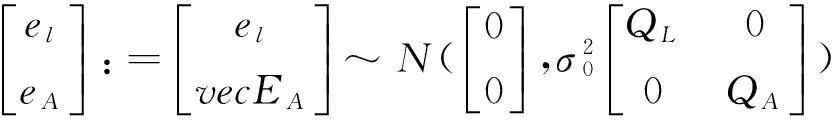
(2)

在同方差的条件下，令

QL=In，QA=Imn

可得

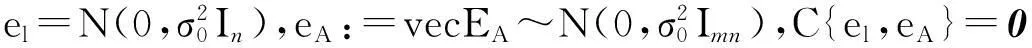
(3)

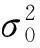
经典TLS问题，就是求解下列约束优化问题[2,5]：

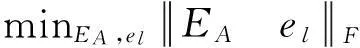
(4)

L-el∈Range(A-EA)。

(5)

1.1基于奇异值分解的算法

为了解决TLS问题，可将式(1)中的EIV模型改写为[6]：

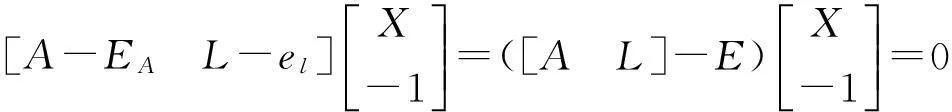
(6)

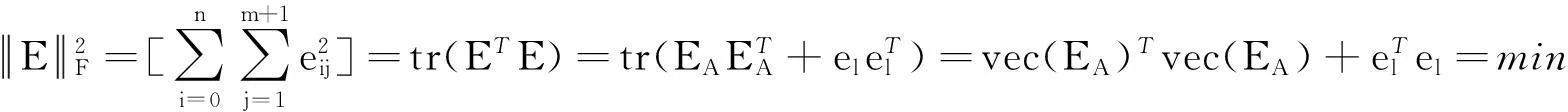
(7)

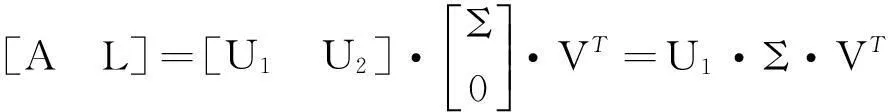
(8)

对上述SVD分解后的矩阵进行分块，即：

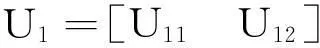
(9)

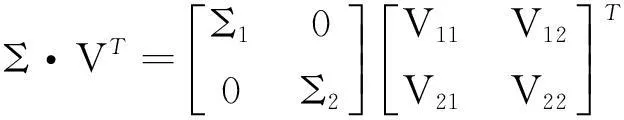
(10)

在式(7)的约束条件下，根据Echart-Young-Mirsky矩阵逼近定理[7]，可得调整后的矩阵：

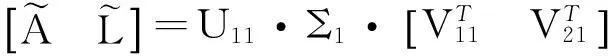
(11)

由式(8)和式(11)，可得出满足式(4)的最小误差矩阵E，即：

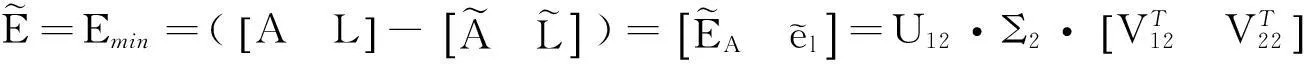
(12)

一个最小二乘解是存在且唯一的，当且仅当V22≠0，σn≠σn+1。在整体最小二乘解存在且唯一的条件下，未知参数的最佳估值为[2]：

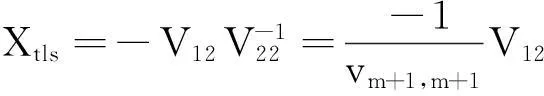
(13)

那么整体最小二乘的奇异值分解(SVD)解算步骤为：

1)给出EIV模型：L=(A-EA)X+el；

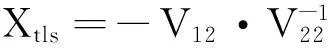
1.2基于传统Lagrange逼近的解算算法

求解TLS问题，使用最广泛的方法就是基于以下目标方程[8]：

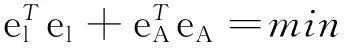
(14)

使得

L-el-AX+EAX=0；

(15)

由上述TLS问题的目标方程，可得Lagrange函数：

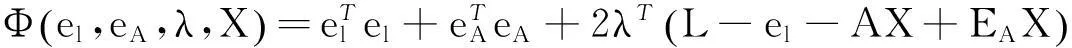
(16)

其中：

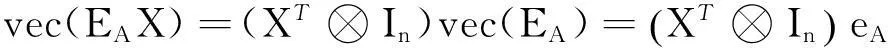
(17)

其中，算子⊗表示Kronecker积。

相应的Euler-Lagrange必要条件为：

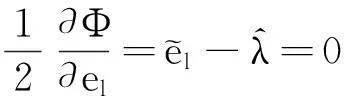
(18a)

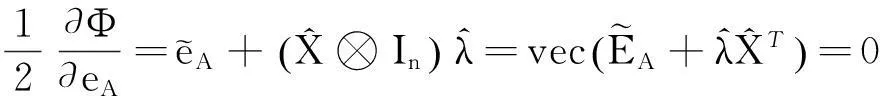
(18b)

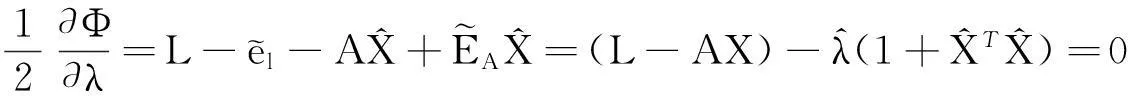
(18c)

(18d)

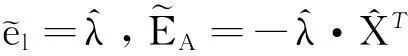
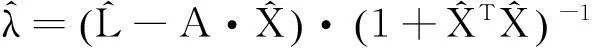
(19)

综合上述各式，易得调整后的误差矩阵：

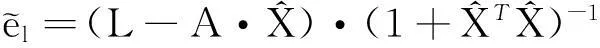
(20)

(21)

因此目标方程(14)可以改写为：

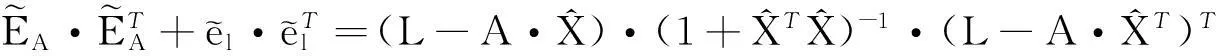
(22)

将式(19)和(21)代入式(18d)，可得[8]

(23)

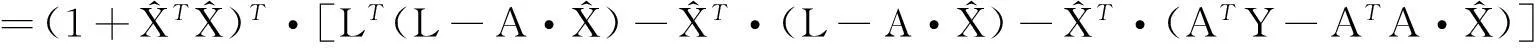
(24)

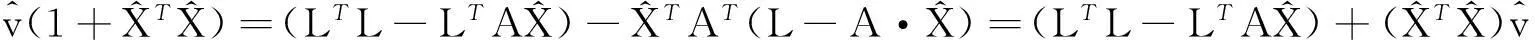
(25)

通过等式(25)，可得

(26)

通过联立等式(13)和(26)，得到了特征值问题(EVP)：

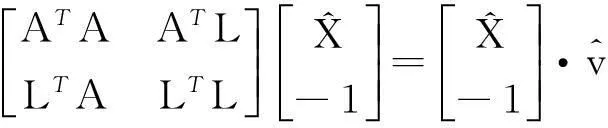
(27)

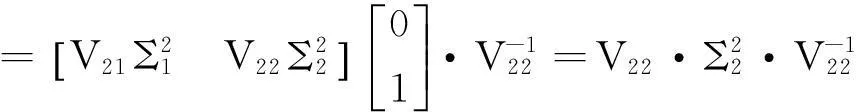
(28)

为了解决TLS问题，将式(23)改写为[6]：

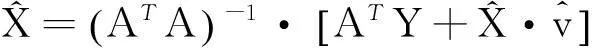
(29)

使用迭代法解决上述TLS问题，解算步骤为：

2)用1)的解作为初始值进行迭代：

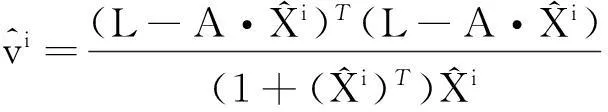
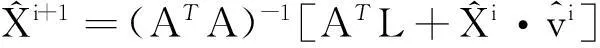
2扩展的TLS

2.1加权整体最小二乘法

根据文献[10]，加权整体最小二乘法(theWeightedTotal-LeastSquares，WTLS)的EIV模型为：

L=(A-EA)X+el，

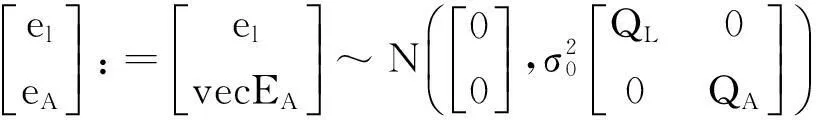
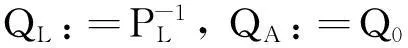
(30)

且

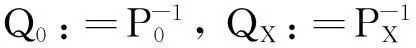
(31)

这里P0为系数矩阵的列向量权阵，PX为系数矩阵的行向量权阵。

在上述条件下计算加权整体最小二乘解，可得目标方程[4]：

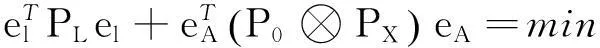
(32)

使得：

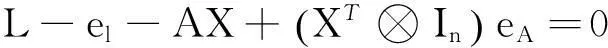
(33)

为了表达出条件(26),对误差矩阵矢量化，使用了恒等式：

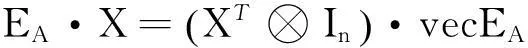
(34)

由传统的Lagrange逼近，可以得到以下的目标方程：

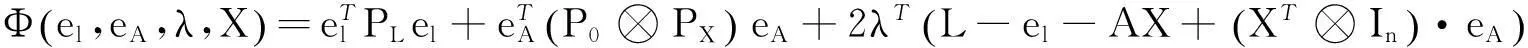
(35)

这里λ是一个n×1维的Lagrange算子，为了计算它的不动点，利用Euler-Lagrange条件[6,9-12]：

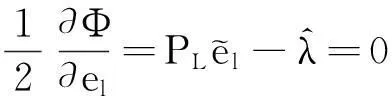
(36a)

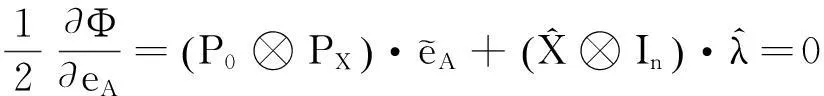
(36b)

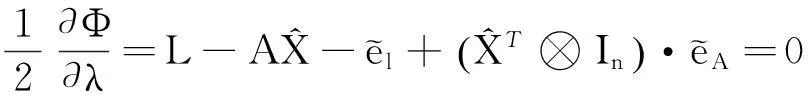
(36c)

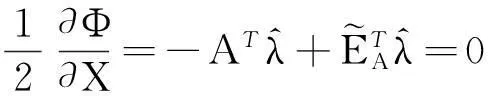
(36d)

实际上，既然有足够条件求解上述等式，那么其解就是要求目标方程(32)的最小值。对目标方程求二阶导数，可以得到Hessian矩阵[10]：

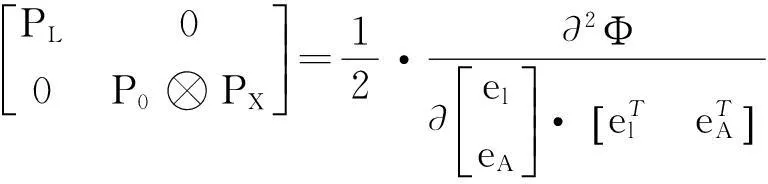
(37)

其为正定矩阵，因此解必然存在。

由(36a)和(36b)可得：

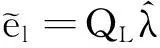
(38)

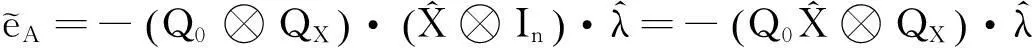
(39)

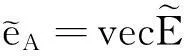
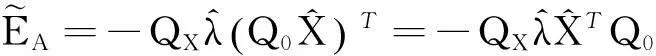
(40)

将(38)、(39)带入(40)中，可得：

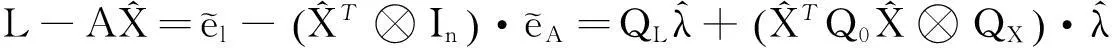
(41)

因此：

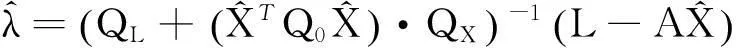
(42)

将(42)重新带入式(38)和(39)中，可得：

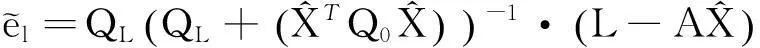
(43)

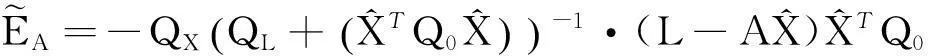
(44)

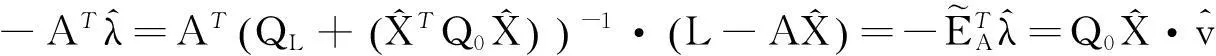
(45)

其中

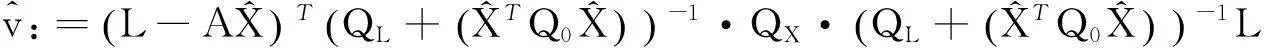
(46)

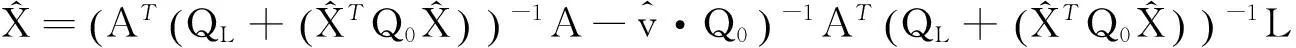
(47)

将式(43)和(44)重新代入目标方程，可以得到加权残差的平方和：

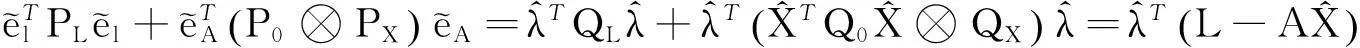
(48)

相应的单位权方差估值为：

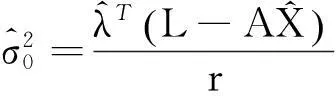
(49)

其中，r是指多余观测或自由度：

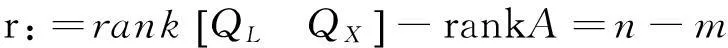
(50)

WTLS问题的迭代解法为：

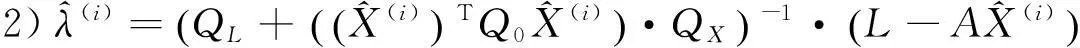
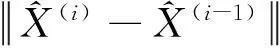
2.2附有约束条件的整体最小二乘法

在建立整体最小二乘模型中，认为未知的参数都是相互独立的。但是实际中，参数估计中遇到存在约束条件的情况，这时引进带有约束条件的整体最小二乘法(theTotalLeastSquareswithConstrains)，将最初的模型(1)加上线性跟二次约束，就变成了以下的带有线性跟二次约束的EIV模型[4,13]：

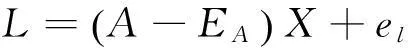
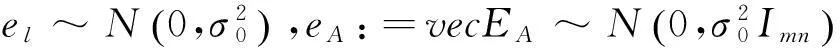
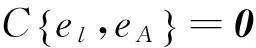
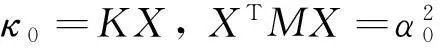
(51)

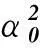
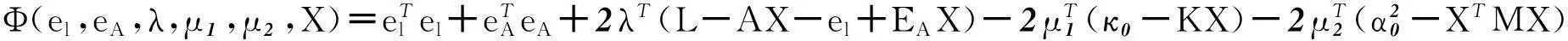
(52)

必要的Euler-Lagrange条件方程为：

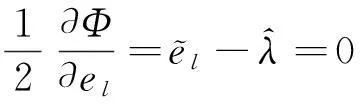
(53a)

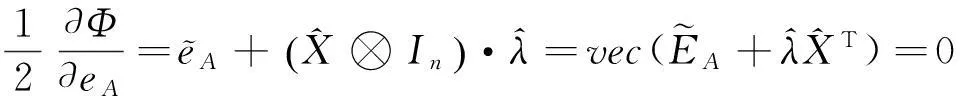
(53b)

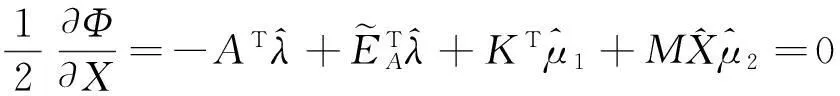
(53c)

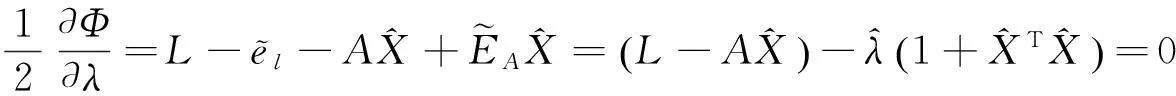
(53d)

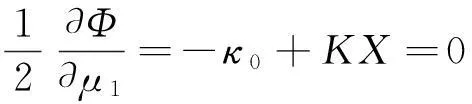
(53e)

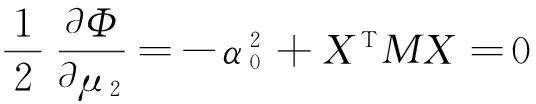
(53f)

令：

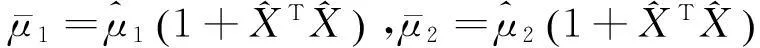
(54)

通过使用(53b)和(53c)的结果，可以得到：

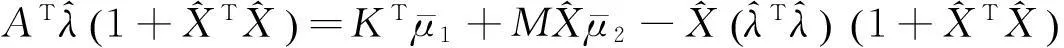
(55)

将(53d)跟(55)联立，可得：

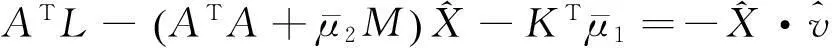
(56)

其中：

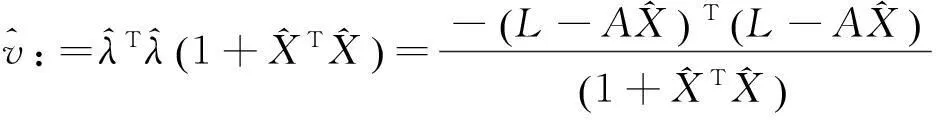
(57)

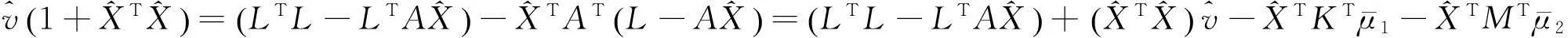
(58)

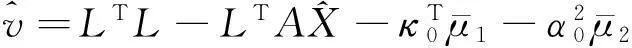
(59)

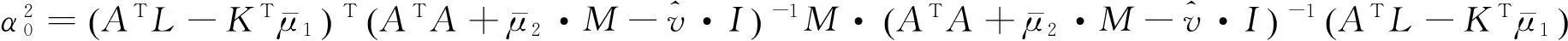
(60)

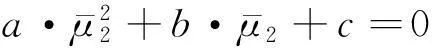
(61)

其中：

可以看出，修正后的特征方程存在多解，需要求如下隐性特征值问题(IEVP)[4]：

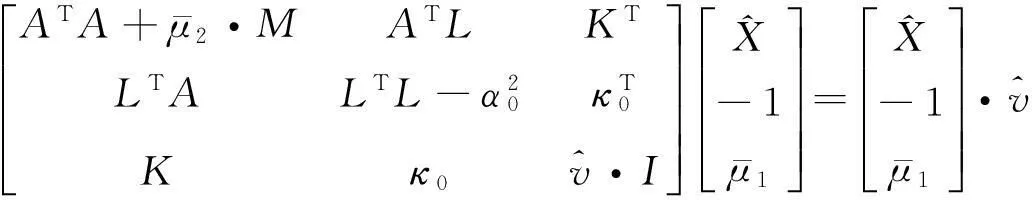
(62)

残差平方和(the sum of squared residuals，SSR)为：

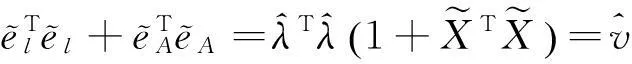
(63)

单位权方差估计公式为：

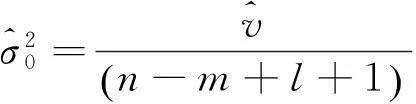
(64)

对于带有线性约束的TLS问题，则解算步骤为：

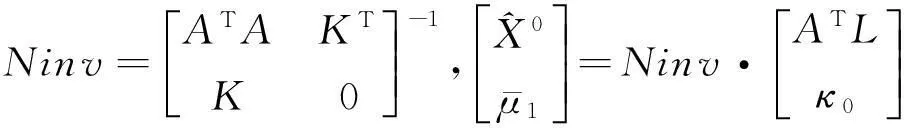
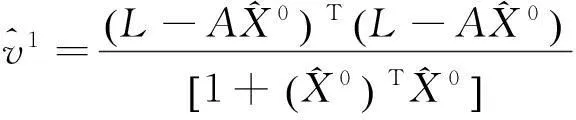
2)

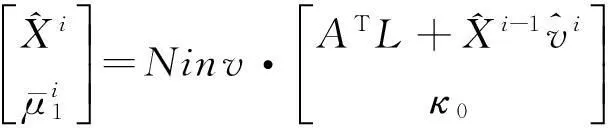
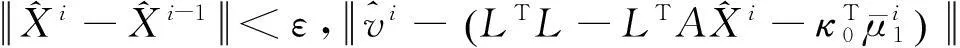
对于带有一个二次约束的TLS问题，则解算步骤为：

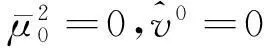
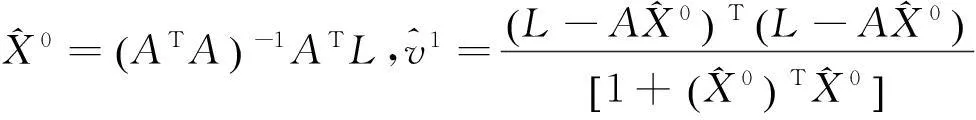
2)

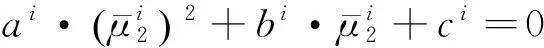
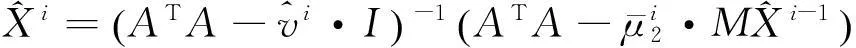
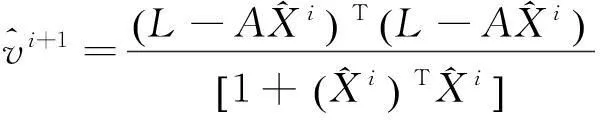
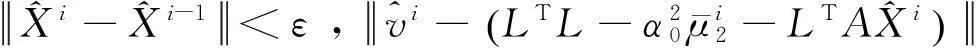
对于带有线性跟二次约束的TLS问题，则解算步骤为：

1)

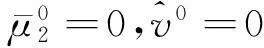
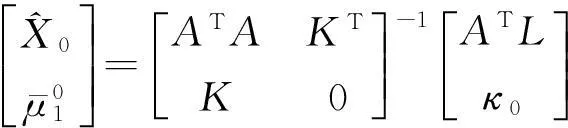
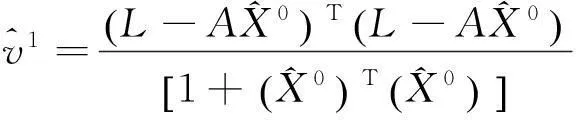
2)

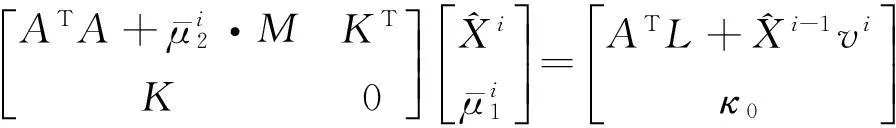
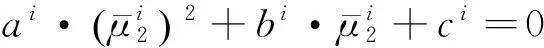
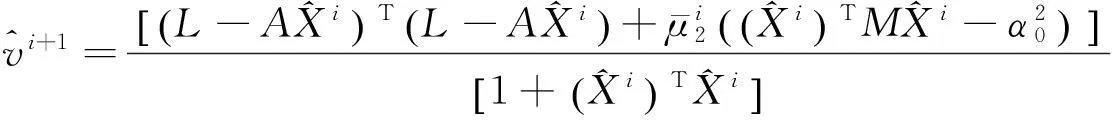
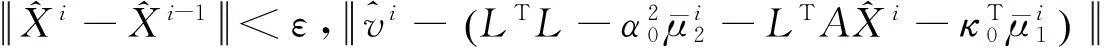
2.3混合整体最小二乘法

实际的线性参数估计当中，系数矩阵部分是由观测值组成，即系数矩阵只有部分存在误差，要解决这类问题就要用到混合整体最小二乘法(LS-TLS)[14]：

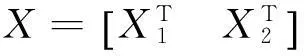
估计数据矩阵误差和观测向量误差，可以得出LS-TLS问题的函数模型：

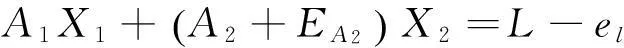
(65)

因此，求解上述LS-TLS方法可表示为求解以下带有约束的优化问题：

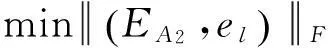
(66)

约束条件为

L-el∈Range(A2+EA2)

式(65)可以改写为：

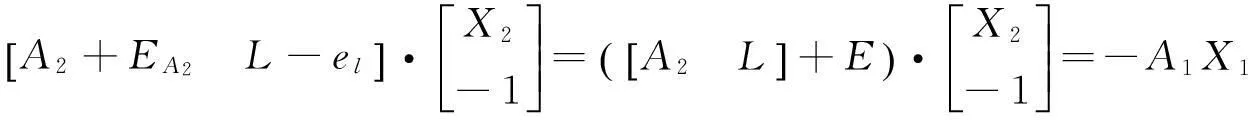
(67)

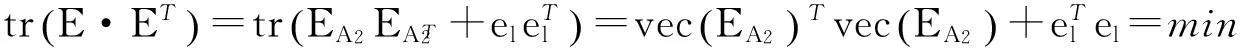
(68)

其中，tr表示矩阵的迹。

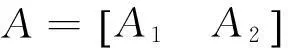
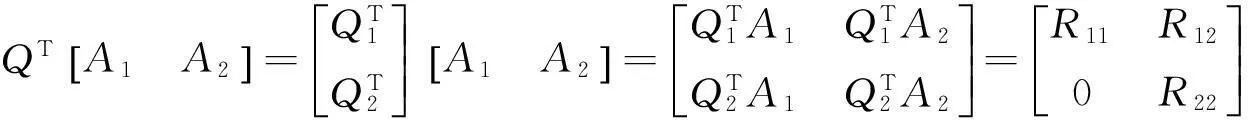
(69)

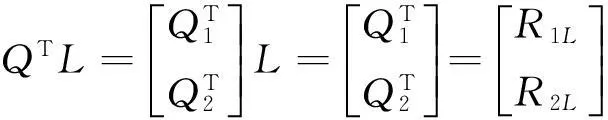
(70)

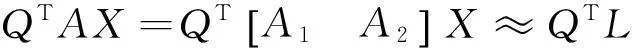
R11X1+R22X2≈R1L；

(71)

R22X2≈R2L；

(72)

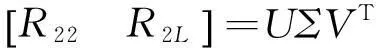
(73)

其中

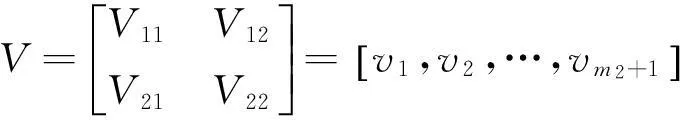
(74)

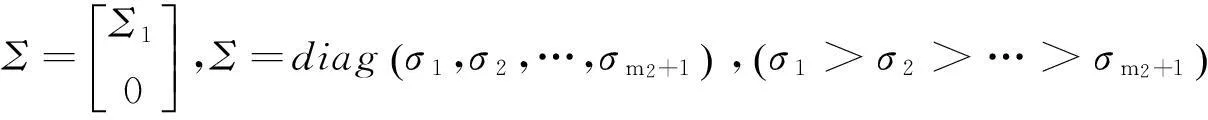
(75)

于是TLS解为：

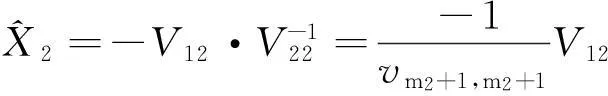
(76)

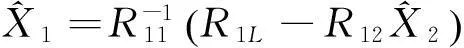
(77)

2.4病态整体最小二乘问题

在EIV模型中，如果系数矩阵的条件数特别大，即使很小的观测误差，也会使待估的参数严重偏离真值。为了解决这种病态的整体最小二乘模型，可以使用Tikhonov正则化理论[15-16]。根据最小二乘正则化模型，整体最小二乘的Tikhonov正则化模型可表示为[17]：

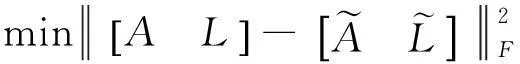
(78)

使得

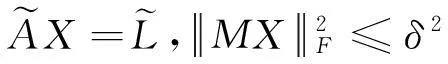
(79)

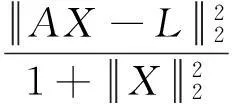
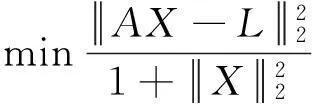
(80)

其中，δ为一任意小常数，M通常为约束矩阵。存在一个参数λ，使得(79)的解满足：

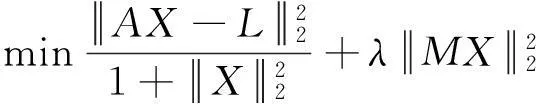
(81)

其中，λ就是整体最小二乘的正则化因子。在文献[17]中，整体最小二乘的正则化解满足：

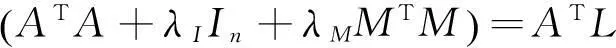
(82)

(ATA+λIMIn)X=ATL。

(83)

其中，λIM=λI+λM。

因此可得到病态TLS问题正则化的迭代解算方法：

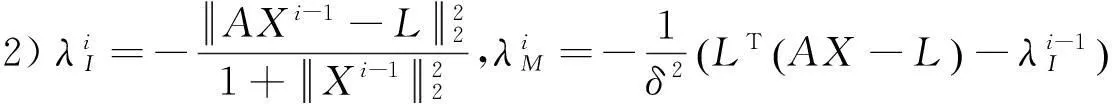
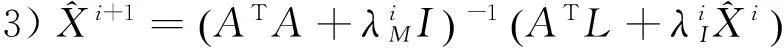
3测量应用

TLS在信号处理、图像处理等众多领域都有着广泛应用[18]。TLS自20世纪80年代起，在数值计算领域得到广泛研究，但是由于其计算过程复杂，大都是纯数学推导，因此在测量领域没有得到广泛应用。在测量领域TLS是从20世纪90年代开始得到逐步应用的[3]。

在测量中，TLS的主要研究领域有：在坐标转换中，针对传统的G-M模型并没有考虑系数矩阵误差[19-20]，学者们陆续开始进行基于TLS的坐标转换研究。文献[21-22]研究了等权观测条件下普通整体最小二乘法在坐标转换中的应用；在相关观测或不等权条件下，文献[9,23-24]研究了基于加权整体最小二乘法的坐标转换。考虑到直线拟合中，自变量和因变量都可能存在误差，且设计矩阵时因部分数据是准确的，因此文献[25]研究了等权条件下基于混合整体最小二乘的直线拟合；针对实测数据中的粗差或异常值，文献[26]提出了稳健整体最小二乘的直线拟合。考虑到实际测量中数据点坐标在x，y，z三个方向上都会存在误差，文献[27]研究了基于整体最小二乘法的空间直线拟合。在利用标靶球方法完成点云配准时，由于点云数据存在误差，因此系数矩阵同样会存在误差，文献[28]提出了基于整体最小二乘的标球定位方法。在空间后方交会解算中，控制点的像片坐标和地面坐标都会存在误差，文献[29]在等权观测条件下研究了整体最小二乘在空间后方交会解算当中的应用。在利用边长变化反演应变参数时，针对LS方法并没有顾及测线方位角量测误差的问题，文献[30-31]在系数矩阵不含有常数列的情况下研究了基于整体最小二乘法的应变参数反演。顾及观测站数目较少和观测噪声较大对定位效果有很大影响的特点，文献[32]基于正则约束整体最小二乘研究了无源测角定位的新算法。在GNSS高程拟合中，针对LS方法并没有考虑高程异常值误差的问题，文献[33-34]分别在等权跟不等权情况下，研究了整体最小二乘法在GNSS高程拟合中的应用。顾及可量测影像的定位定姿观测方程中系数矩阵存在误差且不等权的情况，文献[35]研究了基于加权整体最小二乘的可量测序列影像定位定姿算法。针对遥感图像配准的控制点选取过程中也会存在误差，文献[36]研究了基于加权整体最小二乘法的无人机影像配准。

4结束语

由于在测量领域存在大量观测向量跟系数矩阵都存在着误差的情况，因此20世纪80年代出现的TLS方法在这些情况下得到了成功的应用。故要深入研究TLS在测量数据处理领域的应用，完善测量平差理论体系，得出更加精确的估值。

测量上的病态问题主要表现为解的不稳定性，即观测值或系数矩阵微小的误差都会使解产生很大变化。某些控制网平差、大地测量反演、摄影测量中内外方位元素的解算等方面都是测量中典型的病态问题[37]，在这些情况下TLS方法得出的解是不准确的，因此如何用正则化方法或者截断奇异值方法来解决这些测量上的病态问题，这是在今后大地测量数据处理中该重点考虑的。测量平差中，观测误差还可能含有粗差，粗差是不服从高斯分布的[38]。如果考虑粗差的存在，按TLS方法得到的解将远远偏离真值，影响数据处理的质量。因此，在测量中考虑粗差的时候，如何使用抗差整体最小二乘还需要进行深入研究。

参考文献：

[1]武汉大学测量平差组.误差理论与测量平差基础[M].2版.武汉:武汉大学出版社,2003:71-74.

[2]GLOUBGH,VANLOANFC.Ananalysisofthetotalleastsquaresproblem[J].SIAMJournalonNumericalAnalysis,1980,17(6):883-893.

[3]刘经南,曾文宪,徐培亮.整体最小二乘估计的研究进展[J].武汉大学学报(信息科学版),2013,38(5):505-511.

LIUJingnan,ZENGWenxian,XUPeiliang.Overviewoftotalleastsquaresmethods[J].GeomaticsandInformationScienceofWuhanUniversity,2013,38(5):505-511.

[4]SCHAFFRINB,FELUSYA.Analgorithmicapproachtothetotalleast-squaresproblemwithlinearandquadraticconstrains[J].StudiaGeophysicaetGeodaetica,2009,53:1-16.

[5]MARKOVSKYI,VANHUFFELS.Overviewoftotalleast-squaresmethods[J].SingnalProcessing,2007(87):2283-2302.

[6]SCHAFFRINB,FELUSYA.Onthemultivariatetotalleast-squaresapproachtoempiricalcoordinatetransformations,Threealgorithms[J].JournalofGeodesy,2008(82):373-383.

[7]GLOUBGH,HOFFMANA,STEWARTGW.AgeneralizationoftheEckart-Young-Mirskymatrixapproximationtheorem[J].LinearAlgebraandItsApplication,1987(89):317-327.

[8]SCHAFFRINB,FELUSYA.Multivariatetotalleast-squaresadjustmentforempiricalaffinetransformations[C]//Proceedingsofthe6thHotine-MarussiSymposiumforTheoreticalandComputationalGeodesy.Springer,Berlin,2007:238-242.

[9]MAHBOUBV.Onweightedtotalleast-squaresforgeodetictransformations[J].JournalofGeodesy,2012(86):359-367.

[10]SCHAFFRINB,WIESERA.Onweightedtotalleast-squaresadjustmentforlinearregression[J].JournalofGeodesy,2008(82):415-421.

[11]SHENY,LIB,CHENY.Aninteractivesolutionofweightedtotalleast-squaresadjustment[J].JournalofGeodesy,2011(85):229-238.

[12]MAHBOUBV,SHAIFIMA.Onweightedtotalleast-squareswithlinearandquadraticconstraints[J].JournalofGeodesy,2013(87):279-286.

[13]SCHAFFRINB,FELUSYA.Ontotalleast-squaresadjustmentwithconstraints[C]//AWindowontheFutureofGeodesy[C].BerlinSpringer，2005：417-421.

[14]VANHUFFELS,VANSEWALLEJ.Analysisandpropertiesofthegeneralizedtotalleast-squaresproblemAX=BwhensomeorallcolumnsofAaresubjecttoerrors[J].SIAMJournalonMatrixAnalysisandApplication,1989(10):294-315.

[15]葛旭明,伍吉仓.病态整体最小二乘问题的广义正则化[J].测绘学报,2012,41(3):372-377.

GEXuming,WUJicang.Generalizedregularizationtoill-posedtotalleast-squaresproblem[J].ActaGeodaeticaetCartographicaSinica,2012,41(3):372-377.

[16]王乐洋,许才军,鲁铁定.病态加权总体最小二乘平差的岭估计解法[J].武汉大学学报(信息科学版),2010,35(11):1346-1350.

WANGLeyang,XUCaijun,LUTieding.Ridgeestimationmethodinill-posedweightedtotalleastsquaresadjustment[J].GeomaticsandInformationScienceofWuhanUniversity,2010,35(11):1346-1350.

[17]GLOUBGH,HANSENPC.Tikhonovregularizationandtotalleastsquares[J].SIAMJournalonMatrixAnalysisandApplication,1999,21(1):185-194.

[18]王乐洋,许才军.总体最小二乘研究进展[J].武汉大学学报(信息科学版),2013,38(7):850-856.

WANGLeyang,XUCaijun.Progressintotalleastsquares[J].GeomaticsandInformationScienceofWuhanUniversity,2013,38(7):850-856.

[19]潘国荣,汪大超,周跃寅.两种大转角空间坐标转换模型研究[J].山东科技大学学报(自然科学版),2015,34(1):61-67.

PANGuorong,WANGDachao,ZHOUYueyin.Twospatialcoordinatetransformationmodeloflargeangle[J].JournalofShandongUniversityofScienceandTechnology(NaturalScience),2015,34(1):61-67.

[20]周跃寅,潘国荣,孙海丽.坐标转换解算中基于验前中误差的稳健估计[J].山东科技大学学报(自然科学版),2014,33(3):69-76.

ZHOUYueyin,PANGuorong,SUNHaili.RobustestimationofcoordinatetransferbasedonpriorMSE[J].JournalofShandongUniversityofScienceandTechnology(NaturalScience),2014,33(3):69-76.

[21]孔建,姚宜斌,许双安.整体最小二乘求取坐标转换参数[J].大地测量与地球动力学,2010,30(3):74-78.

KONGJian,YAOYibin,XUShuang’an.Solvingcoordinatetransformationparametersbasedontotalleast-squaresregression[J].JournalofGeodesyandGeodynamics,2010,30(3):74-78.

[22]陆钰,陈义,郑波.总体最小二乘法在三维坐标转换中的应用[J].大地测量与地球动力学,2008,28(5):77-81.

LUJue,CHENYi,ZHENGBo.Applyingtotalleastsquarestothree-dimensionaldatumtransformation[J].JournalofGeodesyandGeodynamics,2008,28(5):77-81.

[23]方兴,曾文宪,刘经南,等.三维坐标转换的通用整体最小二乘算法[J].测绘学报,2014,43(11):1139-1143.

FANGXing,ZENGWenxian,LIUJingnan,etal.Ageneraltotalleastsquaresalgorithmforthree-dimensionalcoordinatetransformations[J].ActaGeodaeticaetCartographicaSinica,2014,43(11):1139-1143.

[24]姚宜斌,黄书华,张良,等.求解三维坐标转换的整体最小二乘新方法[J].武汉大学学报(信息科学版),2015,40(7):853-857.

YAOYibin,HUANGShuhua,ZHANGLiang,etal.AnewmethodofTLSforsolvingtheparametersofthree-dimensionalcoordinatetransformation[J].GeomaticsandInformationScienceofWuhanUniversity,2015,40(7):853-857.

[25]丁克良,沈云中,欧吉坤.整体最小二乘法直线拟合[J].辽宁工程技术大学学报(自然科学版),2010,29(1):44-47.

DINGKeliang,SHENYunzhong,OUJikun.Methodsofline-fittingbasedontotalleast-squares[J].JournalofLiaoningTechnicalUniversity(NaturalScience),2010,29(1):44-47.

[26]官云兰,周世健,张立亭,等.稳健整体最小二乘直线拟合[J].工程勘察,2012(2):60-62.

GUANYunlan,ZHOUShijian,ZHANGLiting,etal.ArobustmethodforfittingalinetopointcloudsbasedonTLS[J].GeotechnicalInvestigationandSurveying,2012(2):60-62.

[27]姚宜斌,黄书华,孔建.空间直线拟合的整体最小二乘算法[J].武汉大学学报(信息科学版),2014,39(5):571-574.

YAOYibin,HUANGShuhua,KONGJian.Totalleastsquaresalgorithmforfittingspatialstraightlines[J].GeomaticsandInformationScienceofWuhanUniversity,2014,39(5):571-574.

[28]鲁铁定,周世健,张立亭,等.基于整体最小二乘的地面激光标靶球定位方法[J].大地测量与地球动力学,2009,19(4):102-105.

LUTieding,ZHOUShijian,ZHANGLiting,etal.SpheretargetfixingofpointclouddatabasedonTLS[J].JournalofGeodesyandGeodynamics,2009,19(4):102-105.

[29]陈义,陆珏,郑波.总体最小二乘方法在空间后方交会中的应用[J].武汉大学学报(信息科学版),2008,33(12):1271-1274.

CHENYi,LUYu,ZHENGBo.Applicationoftotalleastsquarestospaceresection[J].GeomaticsandInformationScienceofWuhanUniversity,2008,99(12):1271-1274.

[30]王乐洋,许才军,鲁铁定.变长变化反演应变参数的总体最小二乘方法[J].武汉大学学报(信息科学版),2010,35(2):181-184.

WANGLeyang,XUCaijun,LUTieding.Inversionofstrainparameterusingdistancechangesbasedontotalleastsquares[J].GeomaticsandInformationScienceofWuhanUniversity,2010,35(2):181-184.

[31]王乐洋.基于总体最小二乘法的大地测量反演理论及应用研究[J].测绘学报,2012,41(4):629-629.

WANGLeyang.Researchontheoryandapplicationoftotalleastsquaresingeodeticinversion[J].ActaGeodaeticaetCartographicaSinica,2012,41(4):629-629.

[32]朱颖童,许锦,赵国庆,等.基于正则约束总体最小二乘无源测角定位[J].北京邮电大学学报,2015,38(6):55-59.

ZHUYingtong,XUJin,ZHAOGuoqing,etal.Passivelocalizationusingbearing-onlymeasurementbasedonregularizedconstrainedtotalleastsquaresalgorithm[J].JournalofBeijingUniversityofPostsandTelecomunications,2015,38(6):55-59.

[33]杨会军.基于整体最小二乘法的GNSS高程拟合研究[J].全球定位系统,2015,40(6):99-101.

YANGHuijun.GNSSheightfittingbasedontotalleastsquares[J].GNSSWorldofChina,2015,40(6):99-101.

[34]赵辉,张书毕,张秋昭.基于加权总体最小二乘法的GPS高程拟合[J].大地测量与地球动力学,2011,31(5):88-96..

ZHAOHui,ZHANGShubi,ZHANGQiuzhao.GPSheightfittingofweightedtotalleast-squaresadjustment[J].JournalofGeodesyandGeodynamics,2011,31(5):88-96.

[35]张晓东,杨元喜,胡庆武,等.可量测序列影像的加权整体最小二乘导航[J].应用科学学报,2013,31(2):147-153.

ZHANGXiaodong,YANGYuanxi,HUQingwu,etal.Weightedgloballeastsquarenavigationbasedonmeasurableimagesequence[J].JournalofAppliedScience,2013,31(2):147-163.

[36]李政,李永树,楚彬,等.基于加权整体最小二乘法的无人机影像配准[J].国土资源遥感,2014,26(2):69-73.

LIZheng,LIYongshu,CHUBin,etal.UAVimageregistrationbasedontheweightedtotalleast-squares[J].RemoteSensingforLandandResources,2014,26(2):69-73.

[37]刘国林,赵长胜,张书毕,等.近代测量平差理论与方法[M].徐州:中国矿业大学出版社,2012:169-170.

[38]靳奉祥.抗差估计理论与方法研究[J].山东科技大学学报(自然科学版),2003,22(4):1-6.

JINFengxiang.Studyonrobustestimationtheoryandmethod[J].JournalofShandongUniversityofScienceandTechnology(NaturalScience),2003,22(4):1-6.

(责任编辑：高丽华)

收稿日期：2016-03-11

基金项目：国家自然科学基金项目(41374009,40974004,40974016)；山东省自然科学基金项目(ZR2013DM009)；国家科技基础性工作专项(2015FY310200)

作者简介：郭金运(1969—)，男，山东巨野人，教授，博士生导师，主要从事空间大地测量、海洋大地测量和物理大地测量等方面的研究工作.E-mail:jinyunguo1@126.com

中图分类号：P207+.1

文献标志码：A

文章编号：1672-3767(2016)04-0001-12

Review on Total Least Squares Methods and Applications in Surveying

GUO Jinyun, XU Xiaofei, SHEN Yi

(College of Geomatics, Shandong University of Science and Technology, Qingdao, Shandong 266590, China)

Abstract:In recent 30 years, the total least squares (TLS) method, a new method for surveying data processing, has been widely applied in telecommunications, geodesy, photogrammetry and image processing. According to the basic theory of TLS, the solutions based on the singular value decomposition and the Lagrange approach were analyzed. Methods to solve the weighted TLS, mixed TLS, the TLS with constraints, and the ill-posed TLS were summarized. Finally, the applications of TLS in surveying were expounded in detail, and the survey data processing theory was complemented.

Key words:total least squares；error-in-variable model；coefficient matrix；singular value decomposition；data processing