何国亮， 张永三

(1.郑州轻工业学院 数学与信息科学学院 河南 郑州 450002；2.河南机电职业学院 人文与艺术设计系 河南 郑州 451191)

Mikhauilov-Novikov-Wang方程族及其bi-Hamilton结构与守恒律

何国亮1， 张永三2

(1.郑州轻工业学院 数学与信息科学学院 河南 郑州 450002；2.河南机电职业学院 人文与艺术设计系 河南 郑州 451191)

借助于零曲率方程得到了与3×3矩阵谱问题相联系的Mikhauilov-Novikov-Wang方程族. 利用迹恒等式和两个斜对称算子, 建立了该族方程的bi-Hamilton结构. 从两个线性谱问题出发给出了Mikhauilov-Novikov-Wang方程的无穷多守恒律.

Mikhauilov-Novikov-Wang方程族； bi-Hamilton结构； 守恒律

0 引言

五阶偏微分方程[1-3]

ut=-uxxxxx+10uuxxx+25uxuxx-20u2ux

(1)

在物理和数学学科中发挥着重要作用. 方程(1)可以从如下的 Mikhauilov-Novikov-Wang (MNW) 方程得到(令v=0)[4]

ut=-uxxxxx+10uuxxx+25uxuxx-20u2ux+9vx,vt=3vuxxx-4u2vx+vxuxx-24uvux.

(2)

因此, MNW 方程的研究可以进一步加深对方程(1)的认识. MNW 方程最初由Mikhauilov、Novikov 和 Wang 通过对称的方法给出，并且他们证明了该方程具有 bi-Hamilton 结构和递归算子. 通过考虑一个 3×3 的矩阵谱问题, 文献[5] 给出了方程 (2) 的一个零曲率表示, 但并未考虑其相应的方程族与守恒率等可积系统的相关问题. 文献[6]考虑了 MNW 方程的相应 Lie 代数，得到了 Lie 代数结构下的方程族及 bi-Hamilton 结构, 但是没有给出方程的无穷守恒律. 本文从零曲率方程出发, 得到了显式的 V 的表示、局部递归算子和方程的无穷多守恒律. 这些性质的取得为考虑方程的显式解提供了思路和工具[7-8].

本文通过探讨与 3×3 矩阵谱问题相联系的零曲率方程，推导出 MNW 方程族，然后借助于该 3×3 矩阵谱问题, 给出该方程族的 bi-Hamilton 结构和方程 (2) 的无穷多守恒律. 本文通过引入Lenard递归方程, 得到了零曲率方程的解的表示,并借助于迹恒等式给出了 MNW 方程族的广义 bi-Hamilton 结构. 通过考虑与方程 (2) 相关的两个线性谱问题，得到了 (2) 式的无穷多守恒律.

1 Mikhauilov-Novikov-Wang方程族

推导与如下 3×3 矩阵谱问题相联系的 MNW方程族

(3)

其中：u,v为位势；λ为常值谱参数. 为了推导相应的非线性演化方程族, 引入两个Lenard递归方程:

(4)

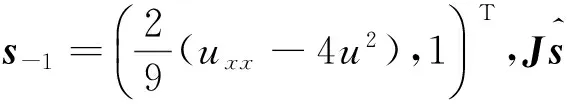
(5)

(6)

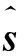
现在来求解驻定零曲率方程

(7)

该方程等价于

V11,x-V21+uV12+(λ+λ-1v)V13=0；V12,x+V11-V22+uV13=0；V13,x+V12-V23=0；

V21,x+u(V22-V11)-V31+(λ+λ-1v)V23=0；V22,x+V21+uV23-uV12-V32=0；

V23,x-uV13-V33+V22=0；V31,x+(λ+λ-1v)(V33-V11)+u(V32-V21)=0；

V32,x-(λ+λ-1v)V12+u(V33-V22)+V31=0；V33,x-(λ+λ-1v)V13+V32-uV23=0.

(8)

其中:

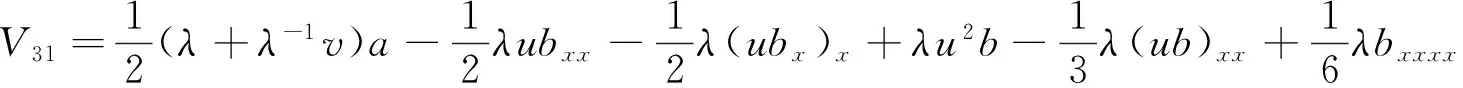
(9)

KSj-1=JSj,j≥0,JS-1=0,

(10)

其中Sj=(aj,bj)T. 因方程JS-1=0的通解为

(11)

则由

(12)

定义的函数Sj满足递归方程(10), 其中:α0、β0为任意常数.

假设ψ满足谱问题式(3) 和如下的辅助谱问题

(13)

(14)

该族非线性演化方程中第一个非平凡的方程为

(15)

如果令α0=9，β0=0，t0=t, 式(15)恰为要研究的方程 (2).

2 广义bi-Hamilton结构

本节将通过迹恒等式来获得式 (14) 的广义bi-Hamilton结构[9-10]，其中迹恒等式为

先计算以下量

(16)

迹恒等式

(17)

其中γ为待定常数, 比较(17)式中λ同次幂的系数可以得到

(18)

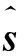
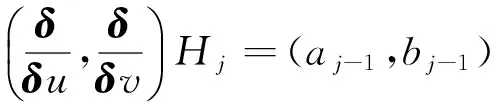
(19)

(20)

3 无穷多守恒律

Φxx+3ΦΦx+Φ3-2uΦ=λ+λ-1v+ux.

(21)

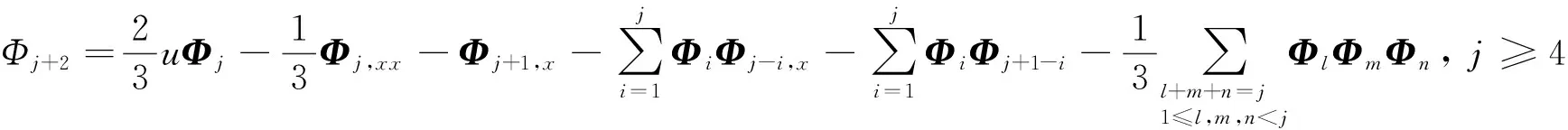
(22)

从辅助谱问题(13)式可得

(23)

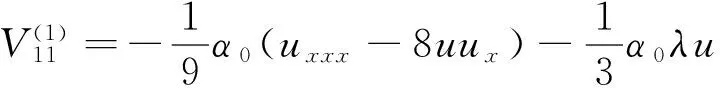
(24)

如果同时把θ展开成λ的级数形式

(25)

从而可得θj的如下表示

(26)

具有多Hamilton结构或无穷多守恒量都是孤子方程可积的重要特征，利用依赖于谱参数的守恒密度的积分在约束条件下求泛函导数的方法可知，无穷多Hamilton泛函与无穷多守恒量之间具有一一对应的关系[11].

[1] KAUP D J. On the inverse scattering problem for cubic eigenvalue problems of the classψxxx+6Q(x)ψx+6R(x)ψ=λψ[J]. Stud Appl Math, 1980, 62(3): 189-216．

[2] KUPERSHMIDT B A. A super Korteweg-De Vries equation: an integrable system [J]. Phys Lett A, 1984, 102(5/6): 213-215．

[3] GENG X G, WU L H, HE G L. Quasi-periodic solutions of the Kaup-Kupershmidt hierarchy [J]. Nonlinear Sci, 2013, 23(4): 527-555．

[4] MIKHAILOV A V, Novikov V S, Wang J P. On classification of integrable nonevolutionary equations [J]. Stud Appl Math, 2007, 118(4): 419-457.

[5] SERGYEYEV A. Zero-curvature representation for a new fifth-order integrable system[J]. Math Sci, 2008, 151(4): 3227-3229．

[6] SHAN X Y, ZHU J Y. The Mikhauilov-Novikov-Wang hierarchy and its Hamiltonian structures [J]. Acta Phys Polonica B, 2012, 43(10): 1953-1963．

[7] 何国亮，杨本朝．扰动Korteweg-de Vries方程的Darboux变换及其显式解[J]. 郑州大学学报(理学版)，2012，44(3)：4-7．

[8] 李雪梅，牛亏环． 广义 TD 族及一些非线性演化方程的显式解[J]. 郑州大学学报(理学版)，2007, 39(3)：1-6．

[9] TU G Z. On Liouville integrability of zero-curvature equations and the Yang hierarchy [J]. J Phys A Math Gen, 1989, 22(13): 2375-2392．

[10]HE G L, GENG X G. An extension of the modified Sawada-Kotera equation and conservation laws [J]. Chin Phys B, 2012, 21(7): 070205．

[11]王燕. 一类孤立子系统的无穷守恒率及Hamilton结构[D]. 郑州：郑州大学，2006．

(责任编辑：方惠敏)

The Mikhauilov-Novikov-Wang Hierarchy,the bi-Hamiltonian Structures and the Conservation Laws

HE Guoliang1， ZHANG Yongsan2

(1.SchoolofMathematicsandInformationScience,ZhengzhouUniversityofLightIndustry,Zhengzhou450002,China; 2.DepartmentofHumanitiesandArtDesign,HenanMechanicalandElectricalVocationalCollege,Zhengzhou451191,China)

The Mikhauilov-Novikov-Wang hierarchy which associated with a 3×3 matrix spectral problem was proposed with the help of the zero-curvature equation. By using the trace identity and two skew-symmetric operators, the bi-Hamiltonian structures of the hierarchy were established. The infinite many conservation laws of the Mikhauilov-Novikov-Wang equation were obtained from two linear spectral problems.

Mikhauilov-Novikov-Wang hierarchy；bi-Hamiltonian structure；conservation laws

2015-11-16

国家自然科学基金资助项目(11501526)；郑州轻工业学院博士基金资助项目(2013BSJJ051)．

何国亮(1983—)，男，河南郑州人，副教授，博士，主要从事孤立子与可积系统研究，E-mail：glhemath@163.com；通讯作者：张永三(1982—)，男，河南平顶山人，讲师，硕士，主要从事孤立子与可积系统研究，E-mail：zyslcczzy@126.com．

何国亮，张永三．Mikhauilov-Novikov-Wang方程族及其bi-Hamilton结构与守恒律[J]．郑州大学学报(理学版)，2016，48(2)：1-4.

O175

A

1671-6841(2016)02-0001-04

10.13705/j.issn.1671-6841.2015263